- Home
- Lớp 1,2,3
- Lớp 1
- Giải Toán Lớp 1
- Tiếng Việt Lớp 1
- Lớp 2
- Giải Toán Lớp 2
- Tiếng Việt Lớp 2
- Văn Mẫu Lớp 2
- Lớp 3
- Giải Toán Lớp 3
- Tiếng Việt Lớp 3
- Văn Mẫu Lớp 3
- Giải Tiếng Anh Lớp 3
- Lớp 4
- Giải Toán Lớp 4
- Tiếng Việt Lớp 4
- Văn Mẫu Lớp 4
- Giải Tiếng Anh Lớp 4
- Lớp 5
- Giải Toán Lớp 5
- Tiếng Việt Lớp 5
- Văn Mẫu Lớp 5
- Giải Tiếng Anh Lớp 5
- Lớp 6
- Soạn Văn 6
- Giải Toán Lớp 6
- Giải Vật Lý 6
- Giải Sinh Học 6
- Giải Tiếng Anh Lớp 6
- Giải Lịch Sử 6
- Giải Địa Lý Lớp 6
- Giải GDCD Lớp 6
- Lớp 7
- Soạn Văn 7
- Giải Bài Tập Toán Lớp 7
- Giải Vật Lý 7
- Giải Sinh Học 7
- Giải Tiếng Anh Lớp 7
- Giải Lịch Sử 7
- Giải Địa Lý Lớp 7
- Giải GDCD Lớp 7
- Lớp 8
- Soạn Văn 8
- Giải Bài Tập Toán 8
- Giải Vật Lý 8
- Giải Bài Tập Hóa 8
- Giải Sinh Học 8
- Giải Tiếng Anh Lớp 8
- Giải Lịch Sử 8
- Giải Địa Lý Lớp 8
- Lớp 9
- Soạn Văn 9
- Giải Bài Tập Toán 9
- Giải Vật Lý 9
- Giải Bài Tập Hóa 9
- Giải Sinh Học 9
- Giải Tiếng Anh Lớp 9
- Giải Lịch Sử 9
- Giải Địa Lý Lớp 9
- Lớp 10
- Soạn Văn 10
- Giải Bài Tập Toán 10
- Giải Vật Lý 10
- Giải Bài Tập Hóa 10
- Giải Sinh Học 10
- Giải Tiếng Anh Lớp 10
- Giải Lịch Sử 10
- Giải Địa Lý Lớp 10
- Lớp 11
- Soạn Văn 11
- Giải Bài Tập Toán 11
- Giải Vật Lý 11
- Giải Bài Tập Hóa 11
- Giải Sinh Học 11
- Giải Tiếng Anh Lớp 11
- Giải Lịch Sử 11
- Giải Địa Lý Lớp 11
- Lớp 12
- Soạn Văn 12
- Giải Bài Tập Toán 12
- Giải Vật Lý 12
- Giải Bài Tập Hóa 12
- Giải Sinh Học 12
- Giải Tiếng Anh Lớp 12
- Giải Lịch Sử 12
- Giải Địa Lý Lớp 12
Trang Chủ ›
Lớp 9›
Giải Bài Tập Toán 9›
Giải Bài Tập Toán 9 Tập 2›
Bài 1. Phương trình bậc nhất hai ẩn Giải toán 9 Bài 1. Phương trình bậc nhất hai ẩn
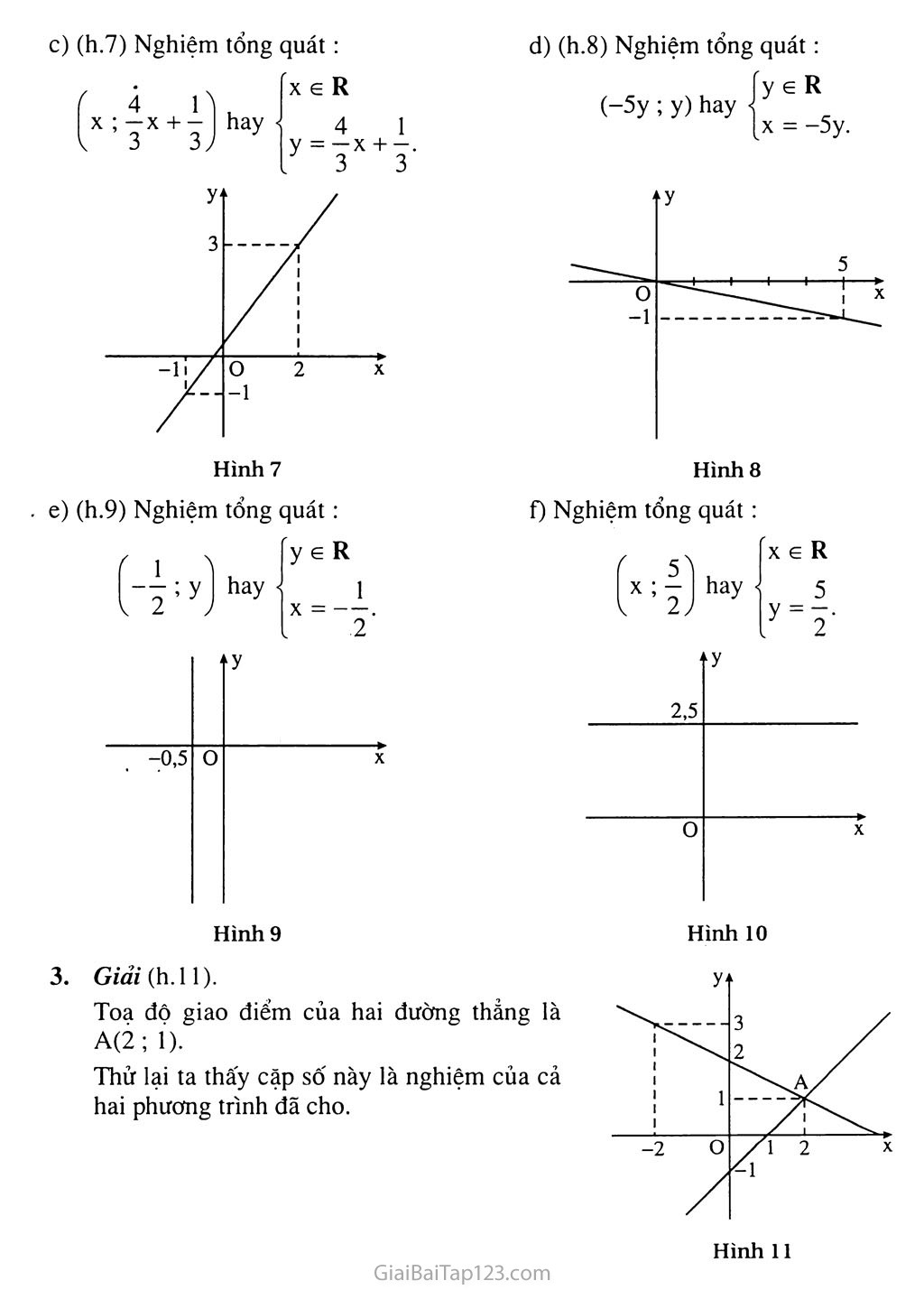
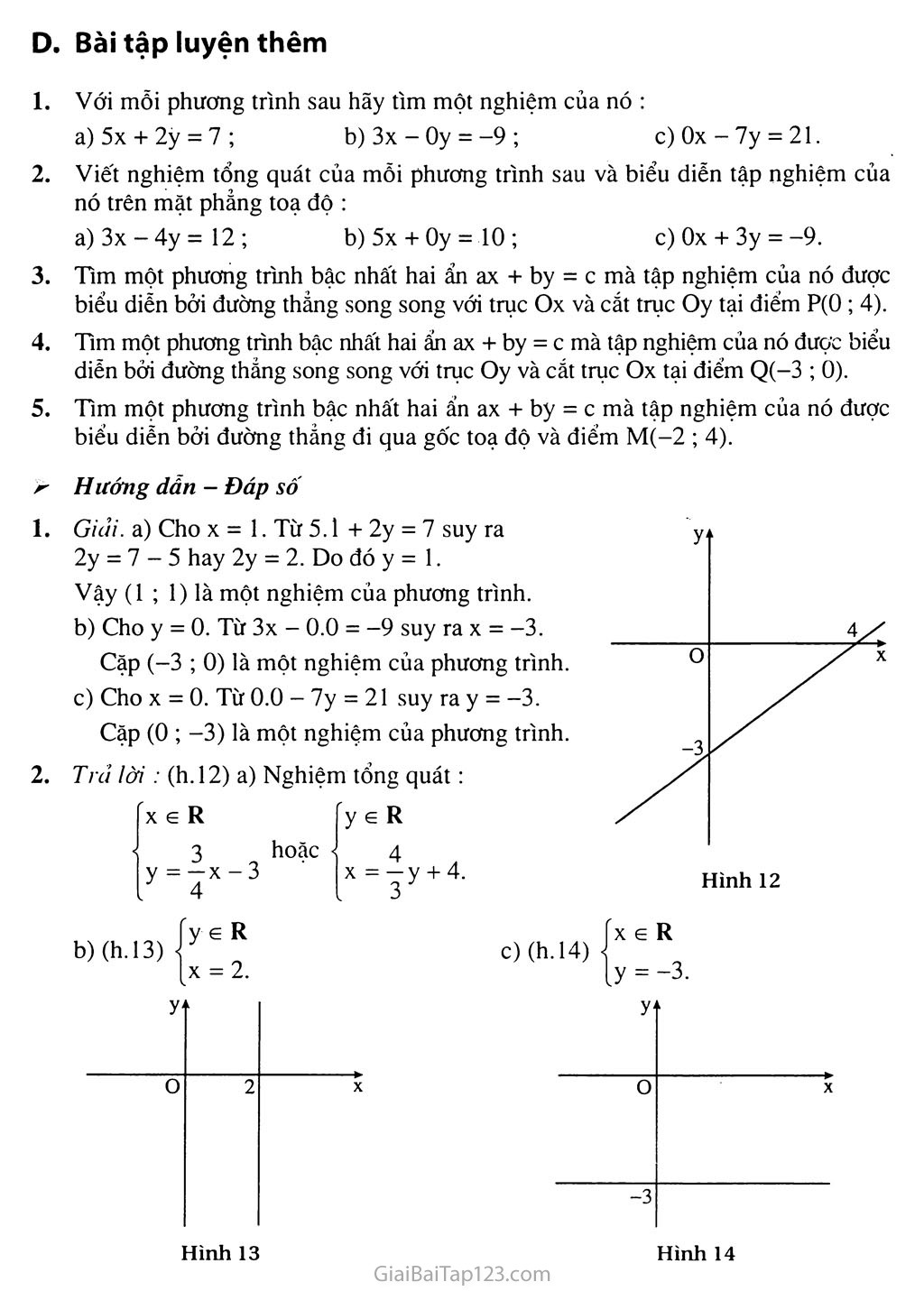
HỆ HAI PHƯƠNG TRINH BẬC NHẤT HAI ẨN §1. PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN A. Tóm tắt kiến thức Khái niệm về phương trình bậc nhất hai ẩn Phương trình bậc nhất hai ẩn X, y là một hệ thức dạng ax + by = c, (1) trong đó a, b, c là những số dã biết, (i/fì hoặc b ^0. Các số a, b, c được gọi lừ các hệ sô' của phương trình này. Nghiệm của phương trình (1) là một cặp số(xn ; yfí) sao cho ' czx0 + by0 = c. Lưu ý. a) Khi (x0 ; ỵfí) là một nghiệm của phương trình (1) ta cũng nói rồng cặp số này tliod mãn phương trình (1). Mỗi nghiệm (x0 ; yfí) của phương trình (1) dược biểu diễn trên mặt phẳng toạ độ bởi một điếm có toạ độ là (x0 ; y0). Muốn tìm một nghiệm của phương trình ax + by = c, ta có thê làm như sau : Nếu d Mi thì ta thay y bởi một giá trị yfí rồi từ ax + by0 = c suy ra giá tri tương ứngXQ của .V. Cặp giá trị tương ứng (xq ; yfí) là một nghiệm của phương trình. Nếu b *0 thì ta thay X bởi một giá tri x0 rồi từ axfì + by = c suy ra giá trị tương ứng V() của y. Cặp giá trị tương ứng (x0 ; yn) lủ một nghiệm của phương trình. Tập nghiệm của phương trình bậc nhất hai ẩn Ta gọi dó là công thức nghiệm tổng quát của phương trình. Tương tự, với mỗi y e R, ta cũng suy ra A' = - — y + — và cũng có nghiệm tổng a a quát là + h“y ' y a a J ;eR b . c X - y+ a a Tập nghiệm của phương trình ax + by = c được biểu diễn bởi dồ thị của hàm sô' bậc nhất a c b b Đó là một đường thẳng cắt cả hai trục toạ độ. • Nếu a = 0 thì với mỗi A e R ta đều có y . A e R c y = T- b Nghiệm tổng quát của phương trình là ^A ; hay ■ Tập nghiệm của phương trình là dường thẳng vuông góc với Oy và cắt Oy tại diêm có tung độ là — . ■ b • Nếu b = 0 thì với mỗi y e R ta đều có A = — . Nghiệm tổng quát của phương trình là ; y j hay Tập nghiệm của phương trình là dường thẳng vuông góc với trục Ox và cắt Ox tại điểm cồ hoành độ là — . a Tổng quát : Tập nghiệm của một phương trình ax + by = c được biểu diễn bởi một đường thẳng. Đường thẳng này được gọi là đường thẳng ax + by = c. Lưu ý. Muốn vẽ dường rlìẳng ax + by = c, ta có thể làm như sau : Nếu a ^0, ta cho A hai giá tri phân biệt XỊ, x2, tính các giá trị tương i'mg y/,y2 ; xác định hai điểm A(xj ; yj), B(x2 ; y2), l ồi kẻ dường thẳng AB. Nếu b *0, ta cho y hai giá tri phân biệt y/,y2, tính các giá trị tương ứng Xj,x2 ; xác định hai điểm A(x/ ; y/), B(x2 ; y2), rồi kẻ dường thẳng AB. B. Ví du Ví dụ 1. Hay cho biết những phương trình nào sau đây là phương trình bậc nhất hai ẩn và chỉ rõ hai ẩn : 3x - 5y = 7 ; 4u + 7v = - 5 ; 6s - 2t = 0 ; X2 - 4y = 1. Giải. Phương trình 3x - 5y = 7 là một phương trình bậc nhất của hai ẩn X và y. Phương trình 4u + 7v = -5 là một phương trình bậc nhất của hai ẩn u và V. Phương trình 6s - 2t = 0 là một phương trình bậc nhất của hai ẩn s và t. Phương trình X2 - 4y = 1 không phải là một phương trình bậc nhất hai ẩn vì bậc của X là 2. Ví dụ 2. Hãy chỉ rõ các hộ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau : 2x + 7y = 5 ; Ox + 5y = -4 ; 3s - Ot = 2 ; 6u - 5v = 0. Giải. Phương trình 2x + 7y - 5 có các hệ số a = 2, b = 7, c = 5. Phương trình Ox + 5y = -4 có các hệ số : a = 0, b = 5 ; c - -4. Phương trình 3s - Ot = 2 có các hệ số: a = 3, b = 0 ; c = 2. Phương trình 6u - 5v = 0 có các hệ số : a = 6, b = -5, c = 0. Ví dụ 3. Cho phương trình 4x - 3y - 6. Xét xem những cặp số nào sau đây là nghiệm của nó ? (3 ; 2); (-6 ; -10); (5 ; -1); fl; ; (-1 ; 4). Phân tích. Muốn biết (3 ; 2) có phải là một nghiệm của phương trình đã cho hay không, ta thay X = 3 ; y = 2 vào phương trình rồi xét xem giá trị hai vế của phương trình có bằng nhau hay không. Giải. Với cập số (3 ; 2), thay X = 3, y = 2 vào phương trình đã cho thì vế trái có giá trị là : 4.3 - 3.2 = 12-6 = 6. Do đó hai vế có cùng giá trị. Vậy cặp số (3 ; 2) là một nghiệm của phương trình. Với cặp số (-6'; -10), vế trái của phương trình đã cho có giá trị là : 4.(-6) - 3.(-10) = -24 + 30 = 6. Do đó hai vế có cùng giá trị. Vậy cặp số (-6 ; -10) là một nghiệm của phương trình. Với cặp số (5 ; -1), vế trái của phương trình đã cho có giá trị là : 4.5 - 3.(-l) = 20 + 3 = 23. Vì vế phải của phương trình là 6 nên hai vế có giá trị khác nhau. Vậy cặp số (5 ; -1) không phải là một nghiệm của phương trình. Với cặp số I Ị; — ỹ I, vế trái của phương trình đã cho có giá trị là : 4.1 -3.1 -j I =4 + 2 = 6. Do đó hai vế có cùng giá trị. Vậy cặp số ự ; - — Ị là một nghiệm của phương trình. Với cặp số (-1 ; 4), vê' trái của phương trình đã cho có giá trị là : 4.(-l) - 3.(4) = -4 - 12 = -16. Vì vế phải của phương trình là 6 nên hai vế có giá trị khác nhau. Vậy cập số (-1 ; 4) không phải là một nghiệm của phương trình. Ví dụ 4. Viết nghiệm tổng quát của mỗi phương trình sau : 7x - 5y = 11 ; 4x - Oy = 19 ; Ox + 5y = 20. > Giải, a) Vì a = 7, b = -5 nên với mỗi X e R, từ 7x - 5y = 11 ta suy ra , _ . , , , 7 11 -5y = -7x + 11 hay y = — X - y . Vậy nghiệm tổng quát của phương trình là hay X e R 7 11 y = Tx - - • 5 5 (Nếu ta lấy một giá trị tuỳ ý y e R thì từ 7x - 5y = 11 suy ra 7x = 5y + 11 hay X = — y + — 7 7 5„ , 11 . „1 yy + y ; y hay và có nghiệm tổng quát là f y e R 5 . 11 X - — y + — 7 7 b) Với mỗi giá trị y 6 R, từ 4x - Oy = 19, ta đều có X = —. 4 Vậy nghiệm tống quát của phương trình là I-y; y I hay c) Với mỗi giá trị X e R, từ Ox + 5y = 20 suy ra y = 4. Vậy nghiệm tổng quát của phương trình là (x ; 4) hay X e R y = 4. Ví dụ 5. Biểu diễn tập nghiệm của phương trình 3x + 2y = 6 trên một mặt phẳng toạ độ. , 3 Giải. (h. 1) Từ 3x + 2y = 6 suy ra y = •" X + 3. Tập nghiệm của phương trình được biếu diễn 4 3 bời đồ thị của hàm số y = X + 3. Cho X = 0, 2 ta có y = -4-0 + 3 = 3. Chọn điểm P(0 ; 3). 2 3 Cho y = 0, ta có 0 = X + 3. Suy ra X = 2. Chọn điểm Q(2 ; 0). Kẻ đường thẳng PQ. Ví dụ 6. Biểu diễn tập nghiệm của phương trình 5x - 3y = 1 trên một mặt phẳng toạ độ. Phân tích. Nếu dùng cách giải như ví dụ 5 thì ta phải vẽ đường thẳng V = -X- — . Khi đó các điểm 3 3 phương trình. Nhưng việc xác định p và Q không thuận lợi. Đê’ vẽ đường thẳng này ta chọn hai điểm khác có toạ độ là những số nguyên. Giải, (h.2) Thay X = 2, ta có 5.2 - 3y = 1. Suy ra 3y = 9. Do đó y = 3. Chọn điểm A(2 ; 3). Thayx = -l,tacó5.(-l)-3y= 1 hay-5-3y= 1. Suy ra y = -2. Chọn điểm B(-l ; -2). Vẽ đường thẳng AB. Ví dụ 7. Biểu diễn tập nghiệm của phương trình Ox + 2y = -4 trên một mặt phảng toạ độ. I ❖ Phán tích. Với mọi X e R, từ Ox + 2y = -4 suy ra y = -2. Như vậy mọi cặp số (x ; -2) đều là nghiệm của phương trình. Mọi điểm có toạ độ (x ; -2) năm phía dưới trục Ox và cách trục Ox một khoảng là 2 đơn vị. Vì thế chúng tạo nên một đường thẳng song song với trục Ox và đi qua điểm (0 ; -2). > Giải, (h.3) Từ Ox + 2y = -4 suy ra y = -2. Vậy tập nghiệm của phương trình đã cho là đường thẳng song song với Ox và cắt Oy tại điểm (0; -2). Ví dụ 8. Biểu diễn tập nghiệm của phương trình 3x - Oy = 9 trên một mặt phẳng toạ độ. ❖ Phân tích. Với mọi y e R, từ 3x - Oy = 9 suy Hình 3 ra X = 3. Như vậy mọi cặp số (3 ; y) đều là y,. nghiệm của phương trình. Mọi điểm có toạ độ (3 ; y) đều nằm bên phải trục Oy và cách trục Oy một khoảng là 3 đơn vị. Vì thế chúng tạo nên một đường thẳng song song với trục Oy và đi qua điểm (3 ; 0). > Giải. (h.4) Từ 3x - Oy = 9 suy ra X = 3. ° Vậy tập nghiệm của phương trình đã cho là đường thẳng song song với Oy và cắt Ox tại điểm (3 ; 0). Hình 4 c. Hướng dẫn giải bài tập trong sách giáo khoa Hướng dần : Thay (x ; y) bởi (-2 ; 1) vào mỗi phương trình rồi so sánh giá trị hai vế của mỗi phương trình. Tương tự đối với các cặp số còn lại. Trả lời : a) (0 ; 2), (4 ; -3) là nghiệm ; b)(-1 ; 0), (4 ; -3) là nghiệm. Hình 5 Hình 6 Giải. a) (h.5) Nghiệm tổng quát : b) (h.6) Nghiệm tổng quát : y e R (h.8) Nghiệm tống quát : (-5y; y) hay X = -5y. f) Nghiệm tổng quát : 5 Hình 10 y e R ■y 2,5 ■y -°’ Giải (h. 11). Toạ độ giao điểm của hai đường thẳng là A(2; 1). Thử lại ta thấy cặp số này là nghiệm của cả hai phương trình đã cho. 0 X 0 X ; y I hay < X = . .2 X ; j I hay Hình 9 D. Bài tập luyện thêm Với mỗi phương trình sau hãy tìm một nghiệm của nó : 5x + 2ý = 7 ; b) 3x - Oy = -9 ; c) Ox - 7y = 21. Viết nghiệm tổng quát của mỗi phương trình sau và biểu diễn tập nghiệm của nó trên mặt phảng toạ độ : a)3x-4y=12; b) 5x + Oy = 10 ; c) Ox + 3y =-9. Tim một phương trình bậc nhất hai ẩn ax + by = c mà tập nghiệm của nó được biểu diễn bởi đường thẳng song song với trục Ox và cắt trục Oy tại điểm P(0 ; 4). Tìm một phương trình bậc nhất hai ẩn ax + by = c mà tập nghiệm của nó được biểu diễn bởi đường thắng song song với trục Oy và cắt trục Ox tại điểm Q(-3 ; 0). Tim một phương trình bậc nhất hai ấn ax + by = c mà tập nghiệm của nó được biểu diễn bởi đường thẳng đi qua gốc toạ độ và điểm M(-2 ; 4). > Hướng dẫn - Đáp số 1. 2. Giải, a) Cho X = 1. Từ 5.1 + 2y = 7 suy ra 2y = 7 - 5 hay 2y = 2. Do đó y = 1. Vậy (1 ; 1) là một nghiệm của phương trình. Cho y = 0. Từ 3x - 0.0 = -9 suy ra X = -3. Cặp (-3 ; 0) là một nghiệm của phương trình. Cho X = 0. Từ 0.0 - ly = 21 suy ra y = -3. Cập (0 ; -3) là một nghiệm của phương trình. Trả lời: (h. 12) a) Nghiệm tổng quát: X G R ‘ 3 ư 4* -3 b) (h.13) ye R X = 2. y y 0 2 X o X -3 c) (h.14) X e R ừ --3. Hình 13 Hình 14 Giải. Vì tập nghiệm biểu diễn bởi đường thẳng song song với trục Ox nên phương trình có dạng Ox + by = c. Vì đường thảng cắt Oy tại điểm P(0 ; 4) nên toạ độ của p thoả mãn phương trình, tức là b.4 = c hay 4b = c. Nếu chọn b = 1, c = 4 thì phương trình Ox + y = 4 có tập nghiệm được biểu diễn bởi đường thẳng đã cho. Giải. Vì tập nghiệm của phương trình được biểu diễn bởi đường thẳng song song với trục Oy nên phương trình có dạng ax + Oy - c. Vì đường thẳng cắt Ox tại điểm Q(-3 ; 0) nên toạ độ của Q thoả mãn phương trình, tức là a.(-3) = c hay -3a = c. Nếu chọn a = 1, c = -3 thì phương trình X + Oy = -3 có tập nghiệm được biểu diễn bởi đường thẳng đã cho. Giải. Vì tập nghiệm được biểu diễn bởi một đường thẳng đi qua 0(0 ; 0) nên a.o + b.o = c. Từ đó suy ra c - 0. Vì đường thẳng đi qua điểm M(-2 ; 4) nèn a.(-2) + b.4 = 0 hay -2a + 4b = 0. Suy ra a - 2b. Nếu chọn b = 1, a = 2 thì phương trình 2x + y - 0 có tập nghiệm được biểu diễn bởi đường thẳng đã cho.
Các bài học tiếp theo
- Bài 2. Hệ hai phương trình bậc nhất hai ẩn
- Bài 3. Giải hệ phương trình bằng phương pháp thế
- Bài 4. Giải hệ phương trình bằng phương pháp cộng đại số
- Bài 5. Giải bài toán bằng cách lập hệ phương trình
- Ôn tập chương III
- Bài 1. Hàm số y = ax2 (a ≠ 0)
- Bài 2. Đồ thị hàm số y = ax2 (a ≠ 0)
- Bài 3. Phương trình bậc hai một ẩn số
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
Các bài học trước
Tham Khảo Thêm
- Giải Bài Tập Toán 9 Tập 1
- Giải Bài Tập Toán 9 Tập 2(Đang xem)
- Giải Toán Lớp 9 - Tập 1
- Giải Toán Lớp 9 - Tập 2
- Giải Toán 9 - Tập 1
- Giải Toán 9 - Tập 2
- Sách Giáo Khoa - Toán 9 Tập 1
- Sách Giáo Khoa - Toán 9 Tập 2
Giải Bài Tập Toán 9 Tập 2
- Phần Đại Số
- Chương III. Hệ hai phương trình bậc nhất hai ẩn
- Bài 1. Phương trình bậc nhất hai ẩn(Đang xem)
- Bài 2. Hệ hai phương trình bậc nhất hai ẩn
- Bài 3. Giải hệ phương trình bằng phương pháp thế
- Bài 4. Giải hệ phương trình bằng phương pháp cộng đại số
- Bài 5. Giải bài toán bằng cách lập hệ phương trình
- Ôn tập chương III
- Chương IV. Hàm số y= ax2 (a ≠ 0) - Phương trình bậc hai một ẩn
- Bài 1. Hàm số y = ax2 (a ≠ 0)
- Bài 2. Đồ thị hàm số y = ax2 (a ≠ 0)
- Bài 3. Phương trình bậc hai một ẩn số
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chươmg IV
- Phần Hình Học
- Chươmg III. Góc với đường tròn
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và đây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Ôn tập chương III
- Chương IV. Hình trụ - Hình nón - Hình cầu
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích của hình trụ
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 3. Hình cầu - Diện tích mặt cầu và thể tích mặt cầu
- Ôn tâp chươmg IV
- Bài tập ôn cuối năm