Giới Hạn Của Dãy Số: Lý Thuyết, Công Thức Và Giải Bài Tập SGK

Warning: mysqli_query(): (HY000/1): Can't create/write to file '/tmp/#sql-temptable-b851-f5824-910b.MAI' (Errcode: 28 "No space left on device") in /opt/bitnami/wordpress/wp-includes/wp-db.php on line 2162

Giới hạn của dãy số là một điểm lý thuyết phổ biến thường có trong đề thi THPT Quốc Gia. Vì vậy việc nắm rõ khái niệm cũng như cách giải bài tập sẽ giúp ích hơn cho các em trong lúc thi. Hãy cùng Marathon Education tìm hiểu kỹ hơn trong bài viết sau đây! 

Lý thuyết giới hạn của dãy số

Dãy số có giới hạn 0

Định nghĩa 1:

Dãy số (un ) có giới hạn bằng 0 khi n dần tới dương vô cực, nếu giá trị tuyệt đối của n có thể nhỏ hơn một số dương nhỏ tùy ý, mọi số hạng của dãy số và kể từ số hạng bất kỳ nào đó trở đi. 

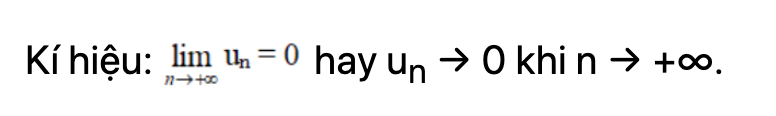
Định nghĩa 2:

Dãy số  (vn) có giới hạn là a (hay vn dần tới a) khi n → +∞ nếu:

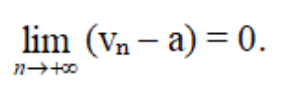
Tính chất: 

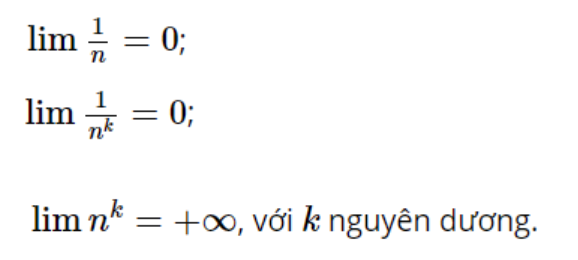
Dãy số có giới hạn vô cực

Dãy số có giới hạn +∞

Dãy số có giới hạn (un ) nếu với mọi số dương bất kỳ, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi đều sẽ lớn hơn số dương đó. 

Ký hiệu: lim un = + ∞. 

Dãy số có giới hạn – ∞

Dãy số có giới hạn (un ) nếu với mọi số âm bất kỳ cho trước, mọi số hạng của dãy số, kể từ một số hạn nào đó trở đi đều sẽ nhỏ hơn số âm đó. 

Ký hiệu: lim un = – ∞.

Các quy tắc tìm giới hạn vô cực 

• Quy tắc nhân

• Quy tắc chia

Dãy số có giới hạn hữu hạn

Định nghĩa:

•  khi và chỉ khi có thể nhỏ hơn một số dương nhỏ tùy ý, kể từ số hạng nào đó trở đi. 
• 

Lý Thuyết Về Phép Biến Hình Lớp 11

ĐĂNG KÝ NGAY

Các định lý: 

1. Nếu lim un = a và lim vn = b, thì:

• lim (un + vn) = a + b.
• lim (un – vn) = a – b.
• lim (un.vn) = ab.
• 

2. Nếu un ≥ 0 với mọi n và lim un = a thì a > 0 và

Các dạng bài tập về giới hạn dãy số có lời giải

 

Dạng 1: Tìm giới hạn của dãy số

Phương pháp giải: Sử dụng định nghĩa, kết hợp tính chất và những định lý về giới hạn của một dãy số

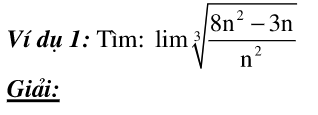
Dạng 3: Chứng minh lim un tồn tại

Phương pháp giải: Sử dụng định lý

• Dãy số (un ) tăng và bị chặn trên thì có giới hạn
• Dãy số (vn ) giảm và bị chặn dưới thì có giới hạn

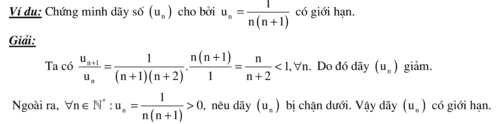
Dạng 4: Tính tổng của cấp số nhân lùi vô hạn

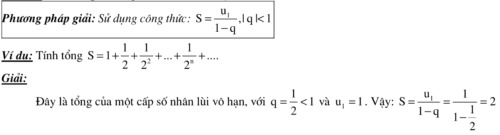
Dạng 5: Tìm giới hạn vô cực

Tham khảo ngay các khoá học online của Marathon Education

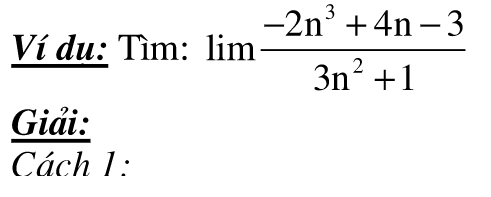
Gia sư Online Học Online Toán 12 Học Online Hóa 10 Học Online Toán 11 Học Online Toán 6 Học Online Toán 10 Học Online Toán 7 Lý Thuyết Toán 10 Giá Trị Lượng Giác Của Một Cung Học Online Lý 10 Học Online Lý 9 Học Online Toán 8 Học Online Toán 9 Học Tiếng Anh 6 Học Tiếng Anh 7

Như vậy, các em đã được tìm hiểu về lý thuyết giới hạn của dãy số cũng như cách giải bài tập đơn giản, chi tiết. Hy vọng với những kiến thức được team Marathon truyền tải, các em có thể dễ dàng ôn luyện và giải bài hiệu quả hơn.

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!