Giới Thiệu Về Hình Học Fractal - VLOS

Tại sao môn hình học được xem là "khô cứng" và "lạnh lẽo"? Một trong lý do cơ bản nhất là vì nó không thể mô tả được thế giới tự nhiên xung quanh chúng ta. Những đám mây trôi lơ lững không phải là những quả cầu, những ngọn núi nhấp nhô không phải là những chóp nón, những bờ biển thơ mộng không phải là những đường tròn. Từ cảm nhận trực quan này, năm 1982, nhà toán học thiên tài Mandelbrot nảy sinh ra ý tưởng về sự tồn tại của một môn "Hình học của tự nhiên", Fractal Geometry. Từ đây, tôi và bạn có thể mô tả một đám mây một cách chính xác như một kiến trúc sư thiết kế căn nhà của họ.

Một fractal là gì? Cho đến giờ các nhà toán học không thể đưa ra khái niệm chính xác. Nhưng ta có thể mô tả một vài đặc trưng chính của nó như sau:

Từ những cảm nhận đầu tiên của Mandelbrot, Fractal là những vật thể hình học có cấu trúc nhưng quá bất thường để có thể mô tả bằng hình học Euclide. Một fractal bao gồm nhiều phần nhưng mỗi phần lại là một hình ảnh copy thu nhỏ của vật thể đó. Ví như một cây sẽ có nhiều cành, và mỗi cành lại có nhiều cành khác... Vì vậy nếu ta cắt một cành ra thì ta sẽ thấy nó rất giống với toàn bộ thân cây. Đặc điểm này của Fractal được gọi là tính tự đồng dạng (self-similar).

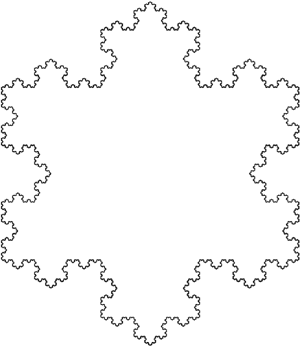
Tính chất quan trọng thứ hai là số chiều Hausdorf lớn hơn số chiều tô pô của nó. Đó là cái gì vậy? Ta hay tưởng tượng, diện tích một hình vuông sẽ tăng lên gấp bao nhiêu lần khi chiều dài cạnh tăng lên 3 lần? Câu trả lời là 9=32. Vậy hãy xem bông hoa tuyết Koch snowflake dưới đây sẽ tăng diện tích lên bao nhiêu lần khi tăng đường kính gấp 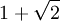lần nhé. Thật đáng ngạc nhiên. Câu trả lời lại là 7 lần. Bới vì chúng ta ghép 6 hình bông hoa tuyết quanh bông hoa đầu tiên thì sẽ được một bông hoa tuyết mới có đường kính... Bạn hãy thử xem!

Ngày nay, các nghiên cứu, ứng dụng thực tế liên quan đến Fractal đang ngày càng tăng như những bông hoa bừng nở khi mùa xuân đến. Từ thị trường chứng khoán đến vật lý thiên văn, từ sinh học đến hóa học đâu đâu người ta cũng thấy bóng dáng của fractal. Các hội thảo, hội nghị quốc tế liên ngành về Fractal ngày càng nhiều. Còn bạn? Bạn có sẳn sàng và có muốn bước vào thế giới kỳ ảo này không?

Đọc thêm[sửa]

• Hình học bội phân (Fractals)

Bài liên quan

• Tỉ lệ logarit
• Vai trò công cụ của logarit qua một số ứng dụng
• Vài nét sơ lược về lịch sử xuất hiện khái niệm logarit
• Vấn đề dạy học logarit trong chương trình toán phổ thông và những điều cần biết về logarit
• Kẻ thất bại và kẻ siêu thất bại

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Hình học bội phân (Fractals)
• Các bức họa hé lộ dấu hiệu sớm của suy giảm nhận thức