Hằng Số Planck – Wikipedia Tiếng Việt

Đối với định luật về bức xạ vật đen, xem Định luật Planck.

Hằng số Planck
Ký hiệu thường gặp	h, hoặc ħ cho hằng số Planck rút gọn
Thứ nguyên	M L 2 T − 1 {\displaystyle {\mathsf {M}}{\mathsf {L}}^{2}{\mathsf {T}}^{-1}}

Giá trị

Hằng số	Đơn vị SI	Đơn vị eV
h	6,62607015×10−34 J⋅Hz−1[1]	4,135667696...×10−15 eV⋅Hz−1[2]
ħ	1,054571817...×10−34 J⋅s[3]	6,582119569...×10−16 eV⋅s[4]
hc	1,98644586...×10−25 J⋅m	1,23984198... eV⋅μm
ħc	3,16152677...×10−26 J⋅m	0,1973269804... eV⋅μm

Hằng số Planck là một hằng số vật lý cơ bản, ký hiệu bằng h {\displaystyle h} , có tầm quan trọng to lớn trong cơ học lượng tử. Năng lượng của một photon bằng tần số của nó nhân với hằng số Planck. Do tương đương khối lượng–năng lượng, hằng số Planck cũng liên hệ giữa khối lượng và tần số.

Trong đo lường học, hằng số Planck, cùng những hằng số khác, được dùng để định nghĩa kilogram, một đơn vị SI.[5] Các đơn vị SI được định nghĩa sao cho khi biểu diễn hằng số Planck trong các đơn vị SI, nó có giá trị đúng bằng h = 6,62607015×10−34 J⋅Hz−1[1][6]

Cuối thế kỷ 19, phổ bức xạ vật đen đã được đo với độ chính xác cao, nhưng phân bố của những phép đo ở tần số cao chênh lệch đáng kể so với những tiên đoán bằng lý thuyết thời bấy giờ. Năm 1900, Max Planck bằng thực nghiệm đưa ra một công thức cho phổ quan sát được. Ông giả sử một hạt tích điện dao động trong một khoảng trống với bức xạ vật đen chỉ có thể thay đổi mức năng lượng của nó theo bước nhỏ E tỷ lệ thuận với tần số của sóng điện từ tương ứng.[7] Bằng kết quả thí nghiệm, ông tính được hằng số tỷ lệ này, và hằng số đó được đặt tên để vinh danh ông. Năm 1905, Albert Einstein xác định mức năng lượng tối thiểu, hay "lượng tử", của một sóng điện từ. Lượng tử ánh sáng có tính chất giống như một hạt không mang điện, và cuối cùng có tên gọi photon. Max Planck nhận Giải Nobel Vật lý năm 1918 cho "những đóng góp của ông cho sự tiến bộ của Vật lý với phát hiện lượng tử năng lượng của ông".

Định nghĩa

[sửa | sửa mã nguồn]

Liên hệ Planck cho biết năng lượng photon E tỷ lệ thuận với tần số tương ứng f, và hằng số tỷ lệ được gọi là hằng số Planck, ký hiệu bằng h:

E = h f . {\displaystyle E=hf.}

Năng lượng này cực kỳ nhỏ so với mức năng lượng của những đồ vật thường ngày.

Vì tần số f, bước sóng λ, và tốc độ ánh sáng c được liên kết với nhau bởi f = c λ {\displaystyle f={\frac {c}{\lambda }}} , hệ thức trên có thể được viết thành

E = h c λ . {\displaystyle E={\frac {hc}{\lambda }}.}

Hằng số Planck rút gọn

[sửa | sửa mã nguồn]

Định nghĩa của hằng số Planck sử dụng đơn vị SI của tần số, tức là hertz, vốn biểu thị một vòng, 360 độ hay 2π radian, mỗi giây. Trong một số trường hợp mà tần số góc (tần số biểu diễn bằng radian trên giây thay vì vòng trên giây, tức hertz) được dùng, người ta thường đưa hệ số 2π vào trong hằng số Planck, dẫn đến hằng số Planck rút gọn. Hằng số Planck rút gọn bằng hằng số Planck chia cho 2π và được ký hiệu bằng ℏ {\displaystyle \hbar } (đọc là "h-bar"):[chú thích 1]

ℏ = h 2 π . {\displaystyle \hbar ={\frac {h}{2\pi }}.}

Bước sóng de Broglie

[sửa | sửa mã nguồn]

Năm 1923, Louis de Broglie tổng quát hóa liên hệ Planck–Einstein với giả thuyết hằng số Planck là hệ số tỷ lệ giữa động lượng và bước sóng lượng tử không chỉ của photon, mà của một hạt bất kỳ. Thực nghiệm sau đó xác nhận giả thuyết này, và nó xuất hiện trong toàn bộ lý thuyết lượng tử, bao gồm điện động học. Bước sóng de Broglie λ của một hạt là

λ = h p {\displaystyle \lambda ={\frac {h}{p}}}

trong đó p là động lượng của một hạt, ví dụ như photon, hoặc bất kỳ hạt sơ cấp nào khác.

Năng lượng của một photon với tần số góc ω = 2πf là

E = ℏ ω , {\displaystyle E=\hbar \omega ,}

còn động lượng thì bằng

p = ℏ k , {\displaystyle p=\hbar k,}

trong đó k là một số sóng góc.

Hai mối liên hệ này là phần thời gian và không gian của biểu thức tương đối hẹp sử dụng 4-vectơ:

P μ = ( E c , p → ) = ℏ K μ = ℏ ( ω c , k → ) . {\displaystyle P^{\mu }=\left({\frac {E}{c}},{\vec {p}}\right)=\hbar K^{\mu }=\hbar \left({\frac {\omega }{c}},{\vec {k}}\right).}

Cơ học thống kê

[sửa | sửa mã nguồn]

Cơ học thống kê cổ điển yêu cầu sự tồn tại của h (nhưng không đưa ra giá trị của nó).[9] Sau phát hiện của Planck, một giả thuyết mới xuất hiện cho rằng tác động vật lý không thể có giá trị bất kỳ, mà phải là bội số nguyên của một đại lượng rất nhỏ, "lượng tử của tác động", nay được gọi là hằng số Planck.[10][chú thích 2] Đây là một ý tưởng cốt yếu trong "thuyết lượng tử cũ" phát triển bởi các nhà vật lý như Bohr, Sommerfeld, và Ishiwara, trong đó tồn tại quỹ đạo hạt nhưng chúng bị ẩn đi, và chúng tuân theo các định luật lượng tử. Quan điểm này đã bị thay thế bởi thuyết lượng tử hiện đại, trong đó quỹ đạo chuyển động thậm chí không tồn tại; một hạt được biểu diễn bằng một hàm sóng trong không gian và thời gian. Cùng với đó là khái niệm lượng tử năng lượng, và cả chuyển động hạt lẫn lượng tử năng lượng đều không thể được giải thích bởi vật lý cổ điển.[11]

Giá trị

[sửa | sửa mã nguồn]

Hằng số Planck có thứ nguyên của mômen động lượng. Trong đơn vị SI, hằng số Planck được biểu diễn bằng joule trên hertz (J⋅Hz−1 hoặc kg⋅m2⋅s−1). Một điểm cần lưu ý trong thứ nguyên của hằng số Planck là việc đơn vị SI của tần số, hertz, biểu diễn một chu kỳ trọn vẹn, 360 độ hay 2π radian, một giây. Tần số góc bằng radian trên giây thường tự nhiên hơn trong toán và vật lý, và nhiều công thức sử dụng hằng số Planck rút gọn.[chú thích 3]

h = 6.626   070   15 × 10 − 34   J ⋅ Hz − 1 {\displaystyle h=6.626\ 070\ 15\times 10^{-34}\ {\text{J}}{\cdot }{\text{Hz}}^{-1}} ℏ = h 2 π = 1.054   571   817... × 10 − 34   J ⋅ s = 6.582   119   569... × 10 − 16   eV ⋅ s {\displaystyle \hbar ={{h} \over {2\pi }}=1.054\ 571\ 817...\times 10^{-34}\ {\text{J}}{\cdot }{\text{s}}=6.582\ 119\ 569...\times 10^{-16}\ {\text{eV}}{\cdot }{\text{s}}}

Các giá trị trên là chính xác và cố định sau lần định nghĩa lại đơn vị cơ bản SI năm 2019.

Cố định giá trị của h

[sửa | sửa mã nguồn] Xem thêm: Định nghĩa lại đơn vị cơ bản SI năm 2019

Từ năm 2019, giá trị của hằng số Planck đã được cố định, với biểu diễn thập phân hữu hạn. Dưới định nghĩa hiện tại của kilogram, phát biểu rằng, "Kilogram [...] được định nghĩa bằng cách cố định giá trị của h bằng 6,62607015×10−34 với đơn vị J⋅s, tương đương với kg⋅m2⋅s−1, trong đó mét và giây được định nghĩa bằng tốc độ ánh sáng c và tần số chuyển siêu tinh tế của trạng thái cơ bản của một nguyên tử caesi-133 ΔνCs."[13] Điều này nghĩa là giá trị của một kilogram, chứ không phải giá trị của hằng số Planck, cần phải được tìm bằng thực nghiệm, bằng những phương pháp như cân Kibble và phương pháp mật độ tinh thể tia X. Để minh họa cụ thể hơn, giả sử quyết định cố định giá trị của h được đưa ra năm 2010. Khi đó, giá trị của h là 6,62606957×10−34 J⋅s, và từ đó giá trị của kilogram cũng được tính từ con số này. Những thực nghiệm trong tương lai sẽ cho thấy giá trị của kilogram lúc ấy bằng 6,62607015/6,62606957 ≈ 1,0000001 lần giá trị của Nguyên mẫu Kilogram Quốc tế (IPK).

Nguồn gốc

[sửa | sửa mã nguồn] Bài chi tiết: Định luật Planck

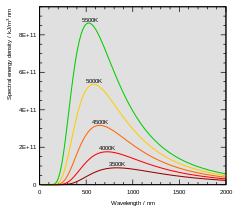
Hằng số Planck xuất phát từ nỗ lực của Max Planck để đưa ra một biểu thức toán học nhằm tiên đoán phổ bức xạ từ một nguồn nhiệt kín, hay bức xạ vật đen.[14] Kết quả là một biểu thức toán học với tên gọi định luật Planck.

Cuối thế kỷ 19, Max Planck xem xét vấn đề bức xạ vật đen do Kirchhoff đưa ra khoảng 40 năm trước đó. Tất cả vật thể vật lý phát ra bức xạ điện từ tự động và liên tục. Không có biểu thức hay lời giải thích nào cho hình dạng của phổ bức xạ quan sát được. Vào lúc đó, định luật Wien khớp với dữ liệu ở bước sóng ngắn và nhiệt độ cao, nhưng sai khác hoàn toàn ở bước sóng dài.[14]:141 Cũng vào thời điểm này, Lord Rayleigh tìm ra một công thức, ngày nay gọi là định luật Rayleigh–Jeans, có thể tiên đoán bước sóng dài tương đối chính xác, nhưng lại không thể giải thích cho bước sóng ngắn.

Planck tiếp cận vấn đề với giải thuyết rằng phương trình chuyển động của ánh sáng miêu tả một tập hợp các dao động điều hòa, mỗi tần số tương ứng với một dao động. Ông xem xét sự thay đổi entropy của những hạt dao động so với nhiệt độ của vật thể, làm cho nó khớp với định luật Wien, và cuối cùng đưa ra một hàm số để xấp xỉ phổ vật đen,[7] dẫn đến một công thức thực nghiệm cho bước sóng dài.

Planck tìm ra một biểu thức khớp với định luật Wien ở bước sóng ngắn và công thức thực nghiệm ở bước sóng dài. Biểu thức này có một hằng số h, được cho là lấy từ Hilfsgrösse (biến phụ),[15] và sau được biết đến là hằng số Planck. Biểu thức cho độ rọi phổ chiếu xạ của một vật đen với tần số ν tại nhiệt độ tuyệt đối T là

B ν ( ν , T ) = 2 h ν 3 c 2 1 e h ν k B T − 1 {\displaystyle B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\mathrm {B} }T}}-1}}}

trong đó kB là hằng số Boltzmann, h là hằng số Planck, và c là tốc độ ánh sáng trong môi trường, có thể là vật liệu hoặc chân không.[16][17][18]

Độ rọi phổ chiếu xạ (tiếng Anh: "spectral radiance") Bν của một vật miêu tả mức năng lượng nó phát ra ở những tần số bức xạ khác nhau. Đại lượng này bằng công suất phát xạ trên một đơn vị diện tích bề mặt, trên một đơn vị góc khối, trên một đơn vị tần số. Độ rọi phổ chiếu xạ cũng có thể được biểu diễn trên một đơn vị bước sóng λ thay vì một đơn vị tần số. Trong trường hợp đó, công thức trên trở thành

B λ ( λ , T ) = 2 h c 2 λ 5 1 e h c λ k B T − 1 , {\displaystyle B_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}},}

cho thấy năng lượng bức xạ ở bước sóng ngắn tăng theo nhiệt độ nhanh hơn so với ở bước sóng dài.[19]

Định luật Planck cũng có thể được biểu diễn theo những đại lượng khác, ví dụ như số photon bức xạ ở bước sóng nhất định, hay là mật độ năng lượng trên một thể tích bức xạ. Đơn vị SI của Bν là W·sr−1·m−2·Hz−1, còn của Bλ là W·sr−1·m−3.

Planck sớm nhận ra rằng lời giải của ông không phải là duy nhất. Một số lời giải khác tồn tại, mỗi cái cho giá trị entropy của các hạt dao động khác nhau.[7] Để giải quyết vấn đề này, Planck dùng đến cơ học thống kê, một ngành còn gây tranh cãi thời bấy giờ,[7] việc mà ông miêu tả là "một hành động tuyệt vọng ... tôi đã sẵn sàng từ bỏ tất cả những niềm tin của mình trong vật lý."[20] Một trong những điều kiện của lời giải này là

coi UN [năng lượng dao động của N hạt] không phải như một đại lượng liên tục, có thể chia nhỏ tùy ý, mà như một đại lượng rời rạc gồm một số nguyên lần những phần tử hữu hạn. Ta gọi mỗi phần năng lượng như thế ε;

— Planck, On the Law of Distribution of Energy in the Normal Spectrum[7]

Với điều kiện mới này, Planck đã lượng tử hóa năng lượng của các hạt dao động, "một giả thuyết hoàn toàn hình thức ... thực tế tôi không nghĩ nhiều về nó ..." theo lời của chính ông.[21] Áp dụng điều kiện này cho định luật Wien cho thấy "phần tử năng lượng" phải tỉ lệ với tần số của dao động, ngày nay gọi là "liên hệ Planck–Einstein":

E = h f . {\displaystyle E=hf.}

Sử dụng dữ liệu bức xạ vật đen từ thí nghiệm, Planck tính được giá trị của h bằng khoảng 655×10−34 J⋅s, sai khác 1,2% so với giá trị chính thức ngày nay.[7] Ông cũng là người đầu tiên xác định giá trị của hằng số Boltzmann kB bằng công thức này.[22]

Phát triển và ứng dụng

[sửa | sửa mã nguồn]

Vấn đề vật đen được xét lại vào năm 1905, khi Rayleigh cùng với Jeans và độc lập với Einstein chứng minh rằng điện từ học cổ điện không thể giải thích phổ bức xạ đo được. Những chứng minh này thường được biết đến với tên gọi "thảm họa cực tím", do Paul Ehrenfest đặt năm 1911. Chúng, cùng với nghiên cứu của Einstein về hiệu ứng quang điện, khiến các nhà vật lý học ngày càng tin rằng việc lượng tử hóa mức năng lượng của Planck có ý nghĩa sâu hơn là một công cụ toán học đơn thuần. hội nghị Solvay đầu tiên năm 1911 có chủ đề "lý thuyết bức xạ và lượng tử".[23]

Hiệu ứng quang điện

[sửa | sửa mã nguồn] Bài chi tiết: Hiệu ứng quang điện

Hiệu ứng quang điện là sự phát xạ electron (gọi là "quang điện tử") từ một bề mặt có ánh sáng chiếu vào. Hiện tượng này lần đầu được quan sát bởi Alexandre Edmond Becquerel năm 1839, mặc dù các nguồn thường ghi nhận Heinrich Hertz,[24] người xuất bản nghiên cứu chi tiết đầu tiên năm 1887. Một nghiên cứu khác của Philipp Lenard (Lénárd Fülöp) được xuất bản năm 1902.[25] Năm 1905, Einstein viết bài báo[26] thảo luận về hiện tượng này bằng lượng tử ánh sáng, một thành tựu đã cho ông giải Nobel Vật lý năm 1921,[24] sau khi những tiên đoán của ông được xác nhận bởi Robert Andrews Millikan.[27]

Trước bài báo của Einstein, bức xạ điện từ như ánh sáng được coi là có hành vi của sóng: đó cũng là nguồn gốc cho các thuật ngữ "tần số" và "bước sóng" dùng để miêu tả các loại bức xạ khác nhau. Năng lượng của một sóng trên một đơn vị thời gian là cường độ. Ánh sáng từ một đèn pha sân khấu có cường độ lớn hơn ánh sáng của một bóng đèn dân dụng, tức đèn pha tỏa ra nhiều năng lượng hơn trên một đơn vị thời gian và một đơn vị không gian, ngay cả khi màu sắc của hai bóng đèn rất giống nhau. Những loại sóng khác như âm thanh hay sóng biển cũng có cường độ của chúng. Tuy nhiên, năng lượng của hiệu ứng quang điện không có tính chất giống như sóng ánh sáng.

Các quang điện tử được phát ra có động năng nhất định, và động năng của mỗi quang điện tử là độc lập với cường độ của ánh sáng,[25] nhưng tỷ lệ thuận với tần số,[27] và nếu tần số quá thấp, sẽ không có quang điện tử nào được phát ra.[28] Giả sử tần số đủ cao để gây ra hiệu ứng quang điện, cường độ nguồn sáng tăng dẫn đến nhiều quang điện tử với cùng động năng được phát ra, thay vì cùng số lượng quang điện tử với động năng lớn hơn.[25]

Einstein giải thích những quan sát này với việc lượng tử hóa ánh sáng: năng lượng ánh sáng không được truyền liên tục dưới dạng sóng, mà chỉ theo những "gói" nhỏ hay lượng tử. Những "gói" năng lượng này, về sau được gọi là photon, có độ lớn bằng những "phần tử năng lượng" của Planck, dẫn đến liên hệ Planck–Einstein:

E = h f . {\displaystyle E=hf.}

Giả thiết của Einstein về sau được chứng minh bằng thực nghiệm: hằng số tỉ lệ giữa tần số nguồn sáng f và động năng của các quang điện tử E bằng với hằng số Planck h.[27]

Cấu trúc nguyên tử

[sửa | sửa mã nguồn] Bài chi tiết: Mô hình Bohr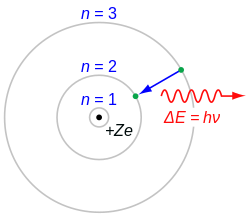

Năm 1912, John William Nicholson giới thiệu h-bar vào lý thuyết nguyên tử và là người đầu tiên lượng tử hóa tần số góc thành h/2π.[29][30][31] Niels Bohr trích dẫn ông trong bài báo mô hình nguyên tử Bohr năm 1913.[32] Ảnh hưởng của mô hình hạt nhân nguyên tử Nicholson lên mô hình của Bohr đã được nhiều nhà sử học nghiên cứu.[33][34][35]

Năm 1913, Niels Bohr đưa ra mô hình lượng tử của nguyên tử thứ ba, nhằm giải quyết những thiếu sót của mô hình Rutherford cổ điển. Mô hình nguyên tử lượng tử đầu tiên được đề xuất bởi Arthur Erich Haas năm 1910 và được thảo luận chi tiết ở Hội nghị Solvay 1911.[36][37] Trong điện từ học cổ điển, một điện tích chuyển động tròn sẽ phát ra bức xạ điện từ. Nếu điện tích đó là một electron quay quanh hạt nhân, bức xạ sẽ khiến nó mất năng lượng và rơi dần vào hạt nhân. Bohr giải quyết nghịch lý này với cảm hứng từ công trình của Planck: một electron trong nguyên tử Bohr chỉ có thể có mức năng lượng định trước En, trong đó

E n = − h c R ∞ n 2 , {\displaystyle E_{n}=-{\frac {hcR_{\infty }}{n^{2}}},}

với c là tốc độ ánh sáng trong chân không, R∞ là hằng số xác định từ thực nghiệm (hằng số Rydberg), và n ∈ {1, 2, 3, ...}. Khi electron đạt mức năng lượng thấp nhất (n = 1), nó không thể tiến gần hơn đến hạt nhân nữa. Phương pháp này cho phép Bohr tính đến công thức Rydberg, một miêu tả thực nghiệm cho phổ nguyên tử của hydro, và giải thích cho giá trị của hằng số Rydberg R∞ bằng những hằng số cơ bản khác.

Bohr cũng đề xuất đại lượng ħ = h / (2π), ngày nay gọi là hằng số Planck rút gọn, làm lượng tử cho mô men động lượng. Ban đầu, Bohr cho rằng đại lượng này là mômen động lượng của mỗi electron trong nguyên tử, nhưng giả thiết này sai, và mặc cho nỗ lực của Arnold Sommerfeld và những người khác, mô hình Bohr không thể miêu tả chính xác mômen động lượng của electron. Quy luật lượng tử hóa tổng quát cho electron – trong đó mô hình Bohr là trường hợp đặc biệt cho nguyên tử hydro – được miêu tả bởi cơ học ma trận của Heisenberg năm 1925 và phương trình sóng Schrödinger năm 1926, và hằng số Planck rút gọn vẫn là lượng tử cơ bản cho mômen động lượng. Cụ thể hơn, nếu J là tổng mômen động lượng của một hệ với bất biến quay và Jz là mômen động lượng đối với một trục bất kỳ, chúng chỉ có thể mang các giá trị

J 2 = j ( j + 1 ) ℏ 2 , j = 0 2 , 1 2 , 2 2 , 3 2 , … , J z = m ℏ , m = − j , − j + 1 , … , j . {\displaystyle {\begin{aligned}J^{2}=j(j+1)\hbar ^{2},\qquad &j={\frac {0}{2}},{\frac {1}{2}},{\frac {2}{2}},{\frac {3}{2}},\ldots ,\\J_{z}=m\hbar ,\qquad \qquad \quad &m=-j,-j+1,\ldots ,j.\end{aligned}}}

Nguyên lý bất định

[sửa | sửa mã nguồn] Bài chi tiết: Nguyên lý bất định

Hằng số Planck cũng xuất hiện trong biểu thức của nguyên lý bất định của Werner Heisenberg. Với nhiều hạt ở cùng trạng thái, sự bất định về vị trí Δx và sự bất định về động lượng Δpx thỏa mãn

Δ x Δ p x ≥ ℏ 2 , {\displaystyle \Delta x\,\Delta p_{x}\geq {\frac {\hbar }{2}},}

trong đó sự bất định được định nghĩa là độ lệch chuẩn của giá trị đo được từ giá trị kỳ vọng. Có một số cặp biến liên hợp đo được khác tuân theo một nguyên lý tương tự, ví dụ như thời gian và năng lượng. Mối quan hệ tỉ lệ nghịch giữa hai độ bất định này dẫn đến một đánh đổi trong các thí nghiệm lượng tử, khi mà càng đo chính xác một đại lượng khiến đại lượng kia càng sai lệch.

Ngoài ra, một trong những nền móng của cơ học lượng tử nằm trong quan hệ giao hoán tử giữa toán tử vị trí x ^ {\displaystyle {\hat {x}}} và toán tử động lượng p ^ {\displaystyle {\hat {p}}} :

[ p ^ i , x ^ j ] = − i ℏ δ i j , {\displaystyle [{\hat {p}}_{i},{\hat {x}}_{j}]=-i\hbar \delta _{ij},}

trong đó δij là Kronecker delta.

Xem thêm

[sửa | sửa mã nguồn]

• CODATA 2018
• Hệ đo lường quốc tế
• Hệ thống đo lường Planck
• Lưỡng tính sóng–hạt

Ghi chú

[sửa | sửa mã nguồn]

1. ^ Đôi khi ℏ {\displaystyle \hbar } được gọi là "hằng số Dirac", theo tên của nhà vật lý Paul Dirac.[8]
2. ^ Đừng nhầm lẫn lượng tử của tác động, tên cũ cho hằng số Planck, với lượng tử của momen góc, tức hằng số Planck rút gọn.
3. ^ Đôi khi ħ còn được gọi là "hằng số Dirac", theo tên Paul Dirac.[12]

Tham khảo

[sửa | sửa mã nguồn]

Chú thích

[sửa | sửa mã nguồn]

1. ^ a b “2018 CODATA Value: Planck constant”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 tháng 5 năm 2019. Truy cập ngày 28 tháng 4 năm 2021.
2. ^ “2018 CODATA Value: Planck constant in eV/Hz”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 tháng 5 năm 2019. Truy cập ngày 29 tháng 4 năm 2021.
3. ^ “2018 CODATA Value: reduced Planck constant”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 tháng 5 năm 2019. Truy cập ngày 28 tháng 8 năm 2019.
4. ^ “2018 CODATA Value: reduced Planck constant in eV s”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 tháng 5 năm 2019. Truy cập ngày 29 tháng 4 năm 2021.
5. ^ International Bureau of Weights and Measures (20 tháng 5 năm 2019), SI Brochure: The International System of Units (SI) (PDF) (ấn bản thứ 9), tr. 131, ISBN 978-92-822-2272-0
6. ^ “Resolutions of the 26th CGPM” (PDF). BIPM (bằng tiếng Anh). 16 tháng 11 năm 2018. Bản gốc (PDF) lưu trữ ngày 19 tháng 11 năm 2018. Truy cập ngày 20 tháng 11 năm 2018.
7. ^ a b c d e f Planck, Max (1901), “Ueber das Gesetz der Energieverteilung im Normalspectrum” (PDF), Ann. Phys., 309 (3): 553–63, Bibcode:1901AnP...309..553P, doi:10.1002/andp.19013090310, lưu trữ (PDF) bản gốc ngày 10 tháng 6 năm 2012, truy cập ngày 15 tháng 12 năm 2008. English translation: “On the Law of Distribution of Energy in the Normal Spectrum”. Bản gốc lưu trữ ngày 18 tháng 4 năm 2008.". “On the Law of Distribution of Energy in the Normal Spectrum” (PDF). Bản gốc (PDF) lưu trữ ngày 6 tháng 10 năm 2011. Truy cập ngày 13 tháng 10 năm 2011.
8. ^ P.R. Bunker; Ian M. Mills; Per Jensen (2019). “The Planck constant and its units”. Journal of Quantitative Spectroscopy & Radiative Transfer. Elsevier. 237: 106594. Bibcode:2019JQSRT.23706594B. doi:10.1016/j.jqsrt.2019.106594. S2CID 201264843.
9. ^ Giuseppe Morandi; F. Napoli; E. Ercolessi (2001), Statistical mechanics: an intermediate course, tr. 84, ISBN 978-981-02-4477-4, lưu trữ bản gốc ngày 6 tháng 12 năm 2021, truy cập ngày 31 tháng 10 năm 2021
10. ^ ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. tr. 133. ISBN 978-0-08-012101-7.
11. ^ Einstein, Albert (2003), “Physics and Reality” (PDF), Daedalus, 132 (4): 24, doi:10.1162/001152603771338742, S2CID 57559543, Bản gốc (PDF) lưu trữ ngày 15 tháng 4 năm 2012, The question is first: How can one assign a discrete succession of energy values Hσ to a system specified in the sense of classical mechanics (the energy function is a given function of the coordinates qr and the corresponding momenta pr)? The Planck constant h relates the frequency Hσ/h to the energy values Hσ. It is therefore sufficient to give to the system a succession of discrete frequency values.
12. ^ P.R. Bunker; Ian M. Mills; Per Jensen (2019). “The Planck constant and its units”. Journal of Quantitative Spectroscopy & Radiative Transfer. Elsevier. 237: 106594. Bibcode:2019JQSRT.23706594B. doi:10.1016/j.jqsrt.2019.106594. S2CID 201264843.
13. ^ International Bureau of Weights and Measures (20 tháng 5 năm 2019), SI Brochure: The International System of Units (SI) (PDF) (ấn bản thứ 9), ISBN 978-92-822-2272-0
14. ^ a b Bitter, Francis; Medicus, Heinrich A. (1973). Fields and particles. New York: Elsevier. tr. 137–144.
15. ^ Boya, Luis J. (2004). "The Thermal Radiation Formula of Planck (1900)". arΧiv:physics/0402064v1. 
16. ^ Planck, M. (1914). The Theory of Heat Radiation. Masius, M. (transl.) (ấn bản thứ 2). P. Blakiston's Son. tr. 6, 168. OL 7154661M.
17. ^ Chandrasekhar, S. (1960) [1950]. Radiative Transfer . Dover. tr. 8. ISBN 978-0-486-60590-6.
18. ^ Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. Wiley. tr. 22. ISBN 978-0-471-82759-7. Lưu trữ bản gốc ngày 27 tháng 7 năm 2020. Truy cập ngày 20 tháng 5 năm 2020.
19. ^ Shao, Gaofeng; và đồng nghiệp (2019). “Improved oxidation resistance of high emissivity coatings on fibrous ceramic for reusable space systems”. Corrosion Science. 146: 233–246. arXiv:1902.03943. doi:10.1016/j.corsci.2018.11.006. S2CID 118927116.
20. ^ Kragh, Helge (1 tháng 12 năm 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com, Bản gốc lưu trữ ngày 8 tháng 1 năm 2009
21. ^ Kragh, Helge (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, tr. 62, ISBN 978-0-691-09552-3, lưu trữ bản gốc ngày 6 tháng 12 năm 2021, truy cập ngày 31 tháng 10 năm 2021
22. ^ Planck, Max (2 tháng 6 năm 1920), The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture), lưu trữ bản gốc ngày 11 tháng 8 năm 2011, truy cập ngày 13 tháng 12 năm 2008
23. ^ Previous Solvay Conferences on Physics, International Solvay Institutes, Bản gốc lưu trữ ngày 16 tháng 12 năm 2008, truy cập ngày 12 tháng 12 năm 2008
24. ^ a b See, e.g., Arrhenius, Svante (10 tháng 12 năm 1922), Presentation speech of the 1921 Nobel Prize for Physics, lưu trữ bản gốc ngày 11 tháng 8 năm 2011, truy cập ngày 13 tháng 12 năm 2008
25. ^ a b c Lenard, P. (1902), “Ueber die lichtelektrische Wirkung”, Ann. Phys., 313 (5): 149–98, Bibcode:1902AnP...313..149L, doi:10.1002/andp.19023130510, lưu trữ bản gốc ngày 18 tháng 8 năm 2019, truy cập ngày 3 tháng 7 năm 2019
26. ^ Einstein, Albert (1905), “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” (PDF), Ann. Phys., 17 (6): 132–48, Bibcode:1905AnP...322..132E, doi:10.1002/andp.19053220607, lưu trữ (PDF) bản gốc ngày 9 tháng 7 năm 2011, truy cập ngày 3 tháng 12 năm 2009
27. ^ a b c Millikan, R. A. (1916), “A Direct Photoelectric Determination of Planck's h”, Phys. Rev., 7 (3): 355–88, Bibcode:1916PhRv....7..355M, doi:10.1103/PhysRev.7.355
28. ^ Smith, Richard (1962), “Two Photon Photoelectric Effect”, Physical Review, 128 (5): 2225, Bibcode:1962PhRv..128.2225S, doi:10.1103/PhysRev.128.2225.Smith, Richard (1963), “Two-Photon Photoelectric Effect”, Physical Review, 130 (6): 2599, Bibcode:1963PhRv..130.2599S, doi:10.1103/PhysRev.130.2599.4.
29. ^ John Heilbron, "The path to the quantum atom," 6 June 2013, Vol 498, NATURE, 27.
30. ^ J. W. Nicholson, Month. Not. Roy. Astr. Soc. lxxii. pp. 49,130, 677, 693, 729 (1912).
31. ^ The Atomic Theory of John William Nicholson, Russell McCormmach, Archive for History of Exact Sciences, Vol. 3, No. 2 (25.8.1966), pp. 160-184 (25 pages), Springer.
32. ^ On the Constitution of Atoms and Molecules, Niels Bohr, Philosophical Magazine, Series 6, Volume 26 July 1913, p. 1-25
33. ^ T. Hirosige and S. Nisio, "Formation of Bohr's Theory of Atomic Constitution," Jap. Studies Hist. Sci, No. 3 (1964), 6-28;
34. ^ J. L. Heilbron, A History of Atomic Models from the Discovery of the Electron to the Beginnings of Quantum Mechanics, diss. (University of California, Berkeley, 1964).
35. ^ R. McCormmach, "The Atomic Theory of John William Nicholson," Arch. Hist. Exact Sci., 3 (1966), 160-184.
36. ^ John Heilbron, "The path to the quantum atom," 6 June 2013, Vol 498, NATURE, 29-30.
37. ^ Bohr, Niels (1913), “On the Constitution of Atoms and Molecules”, Phil. Mag., 6th Series, 26 (153): 1–25, Bibcode:1913PMag...26..476B, doi:10.1080/14786441308634993, lưu trữ bản gốc ngày 27 tháng 1 năm 2020, truy cập ngày 3 tháng 7 năm 2019

Nguồn

[sửa | sửa mã nguồn]

• Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega – The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8

Liên kết ngoài

[sửa | sửa mã nguồn]

• "The role of the Planck constant in physics" – presentation at 26th CGPM meeting at Versailles, France, November 2018 when voting took place.

Tiêu đề chuẩn	GND: 4174790-2