Hình Chữ Nhật – Wikipedia Tiếng Việt

Trang chủ » Hình Chữ Nhật Không Có Tính Chất Nào Sau đây » Hình Chữ Nhật – Wikipedia Tiếng Việt

Có thể bạn quan tâm

Hình chữ 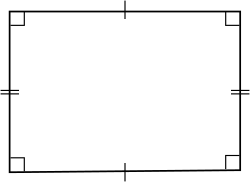nhật
Hình chữ nhật
Loạitứ giác, hình bình hành, Hình Hộp
Số cạnh và đỉnh4
Ký hiệu Schläfli{ } × { }
Biểu đồ Coxeter
Nhóm đối xứngThị diện (D2), [2], (*22), order 4
Dual polygonHình thoi
Tính chấtconvex, isogonal, cyclic Opposite angles and sides are congruent
Hình chữ nhật ABCD với hai đường chéo

Hình chữ nhật trong hình học Euclid là một hình tứ giác có bốn góc vuông.[1] Từ định nghĩa này, ta thấy hình chữ nhật là một tứ giác lồi có bốn góc vuông hay hình bình hành có một góc vuông.

Tên gọi

[sửa | sửa mã nguồn]

Hình này được gọi là "hình chữ nhật" vì có hình dáng giống chữ 日 (Nhật) trong chữ Hán.

Tính chất

[sửa | sửa mã nguồn]
  • Có tất cả các tính chất của hình thang cân và hình bình hành.
  • Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường, đồng thời tạo thành 4 tam giác cân.
  • Nội tiếp đường tròn có tâm là tâm của hình.

Trong tích phân

[sửa | sửa mã nguồn]

Trong toán học tích phân, tích phân Riemann có thể được xem là một giới hạn của tổng số các diện tích của nhiều hình chữ nhật với một chiều ngang cực nhỏ.

Diện tích hình chữ nhật

[sửa | sửa mã nguồn]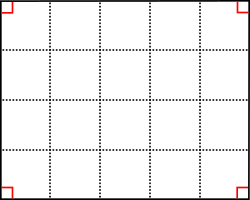
Một hình chữ nhật với chiều dài 4 và chiều rộng 5

Diện tích hình chữ nhật bằng tích của chiều dài và chiều rộng:

S = a × b {\displaystyle S=a\times b}

(trong đó, hai cạnh đối và song song với nhau, chiều dài là a và chiều rộng là b)

Chu vi

[sửa | sửa mã nguồn]

Chu vi hình chữ nhật bằng hai lần tổng chiều dài và chiều rộng của nó:

P = ( a + b ) × 2 {\displaystyle P=\left(a+b\right)\times 2}

Dấu hiệu nhận biết hình chữ nhật

[sửa | sửa mã nguồn]
  • Tứ giác có ba góc vuông là hình chữ nhật.
  • Hình thang cân có một góc vuông là hình chữ nhật.
  • Hình bình hành có một góc vuông là hình chữ nhật.
  • Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Hệ quả

[sửa | sửa mã nguồn]
  • Nếu một tam giác có đường trung tuyến ứng với cạnh đối diện và bằng nửa cạnh ấy thì đó là tam giác vuông.
  • Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền, một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.

Chú thích

[sửa | sửa mã nguồn]
  1. ^ Từ điển toán học thông dụng, trang 316. Tác giả Ngô Thúc Lanh - Đoàn Quỳnh - Nguyễn Đình Trí. Nhà xuất bản giáo dục, năm 2000

Liên kết ngoài

[sửa | sửa mã nguồn] Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Hình chữ nhật.
Hình tượng sơ khai Bài viết liên quan đến toán học này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn.
  • x
  • t
  • s

Từ khóa » Hình Chữ Nhật Không Có Tính Chất Nào Sau đây