Hình Trụ, Hình Nón, Hình Cầu - Hình Học 9 - Gia Sư Tiến Bộ - Abcdonline

Trang chủ » Diện Tích Hình Nón Trụ Cầu » Hình Trụ, Hình Nón, Hình Cầu - Hình Học 9 - Gia Sư Tiến Bộ - Abcdonline

Có thể bạn quan tâm

Hình trụ, hình nón, hình cầu – Hình học 9

Khái niệm, công thức tính diện tích xung quanh, diện tích toàn phần, thể tích của hình trụ, hình nón, hình cầu.

A. Hình trụ

1. Khái niệm hình trụ

Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta thu được một hình trụ.

Hình trụ, hình nón, hình cầu - Hình học 9

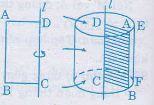
– Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.

– DC là trục của hình trụ.

– Các đường sinh của hình trụ( chẳng hạn EF) vuông góc với hai mặt đáy.

Độ dài đường sinh cũng là độ dài đường cao của hình trụ.

2. Diện tích xung quanh, toàn phần của hình trụ

\displaystyle {{S}_{xq}}=2\pi rh

– Diện tích toàn phần của hình trụ: \displaystyle {{S}_{tp}}=2\pi rh+2\pi r_{{}}^{2}

(r: là bán kính đường tròn đáy, h là chiều cao)

3. Thể tích hình trụ

Công thức tính thể tích hình trụ: \displaystyle V=Sh=\pi r_{{}}^{2}h

(S là dịch tích đáy, h: là chiều cao)

B. Hình nón

1. Khái niệm hình nón

Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.

Hình trụ, hình nón, hình cầu - Hình học 9

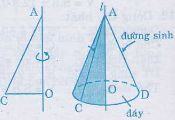
– Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.

– Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .

– A là đỉnh và AO là đường cao của hình nón.

2. Diện tích xung quanh, diện tích toàn phần của hình nón

Diện tích xung quanh của hình nón: \displaystyle {{S}_{xq}}=2\pi rl

Diện tích toàn phần của hình nón: \displaystyle {{S}_{tp}}=\pi rl+\pi r_{{}}^{2}

(r là bán kính đường tròn đáy, l là đường sinh)

3. Thể tích hình nón

Công thức tính thể tích hình nón: Vnón = \displaystyle \pi r_{{}}^{2}h

Diện tích toàn phần của hình nón: \displaystyle {{S}_{tp}}=\pi rl+\pi r_{{}}^{2}

(r là bán kính đường tròn đáy, l là đường sinh)

Hình trụ, hình nón, hình cầu - Hình học 9

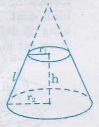
4. Thể tích hình nón cụt

Công thức tính thể tích hình nón: Vnón = \displaystyle \frac{1}{3}\pi r_{{}}^{2}h

C. Hình cầu

1. Khái niệm hình cầu

Khi quay nửa hình tròn tâp O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.

Hình trụ, hình nón, hình cầu - Hình học 9

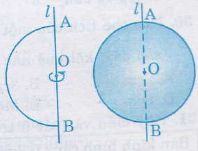
– Điểm O được gọi là tâm, độ dài R là bán kính của hình cầu.

– Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu

2. Diện tích mặt cầu

Công thức diện tích mặt cầu: \displaystyle S=4\pi r_{{}}^{2}=\pi d_{{}}^{2}

R là bán kính, d là đường kính mặt cầu.

3. Thể tích hình cầu

Thể tích hình cầu bán kính R : \displaystyle V=\frac{4}{3}\pi r_{{}}^{3}

Hình học 9 - Tags: diện tích mặt cầu, diện tích xung quanh, hình cầu, hình nón, hình nón cụt, hình trụ, thể tích hình cầu, thể tích hình nón, thể tích hình trụ, toán 9

  • Bảng tỉ số lượng giác các góc đặc biệt – Hình học 9

  • Hệ thức về cạnh và góc trong tam giác vuông

  • 30 bài tập hình học ôn thi vào 10 môn Toán

  • 9 cách chứng minh hai đường thẳng song song – Toán lớp 9

  • Công thức tính độ dài cạnh, độ lớn góc, diện tích các hình

  • Các dạng toán đường tròn lớp 9

  • Lý thuyết đường tròn lớp 9 đầy đủ nhất

Từ khóa » Diện Tích Hình Nón Trụ Cầu