Học Toán 9 Tập 2: Vẽ Hai Dây Cung AB, AD Của đường Tròn (O ; R)

Ôn tập chương 3 - Hình học 9 - Bài 2 trang 113 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Vẽ hai dây cung AB, AD của đường tròn (O ; R)

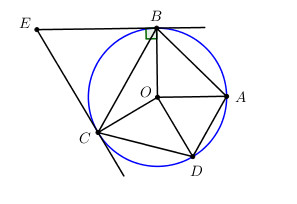
Vẽ hai dây cung AB, AD của đường tròn (O ; R) thỏa mãn AB = \(R\sqrt 2 \) , AD = R và tia AO nằm giữa hai tia AB, AD. Vẽ dây cung BC song song với AD.

a) Tính số đo các cung  AD, AB, BC.

b) Tứ giác ABCD là hình gì?

c) Các tiếp tuyến tại B và tại C cắt nhau tại E. Chứng minh rằng tam giác EBC là tam giác đều.

a) Tính các góc \(\widehat {AOD};\,\,\widehat {AOB};\,\,\widehat {BOC}\) và sử dụng định lí Số đo góc ở tâm bằng số đo cung bị chắn.

b) Chứng minh ABCD là hình thang có 2 góc ở đáy bằng nhau.

c) Chứng minh tam giác EBC là tam giác cân có 1 góc bằng 600.

 

a) Xét tam giác OAB có: \(O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2} = A{B^2} \Rightarrow \Delta OAB\) vuông tại O (Định lí Pytago đảo)  (Số đo góc ở tâm bằng số đo cung bị chắn).

Xét tam giác OAD có: \(OA = OD = AD = R \Rightarrow \Delta OAD\) đều \( \Rightarrow \widehat {AOD} = {60^0} = sdcung\,AD\)  (Số đo góc ở tâm bằng số đo cung bị chắn).

Advertisements (Quảng cáo)

Ta có: AD//BC \( \Rightarrow cung\,AB = cung\,CD \Rightarrow sdcung\,CD = {90^0}\) (2 cung bị chắn giữa 2 dây song song).

\( \Rightarrow \widehat {COD} = {90^0}\)(Số đo góc ở tâm bằng số đo cung bị chắn).

Mà \(\widehat {AOB} + \widehat {BOC} + \widehat {COD} + \widehat {AOD} = {360^0}\)

\( \Rightarrow {90^0} + \widehat {BOC} + {90^0} + {60^0} = {360^0} \Rightarrow \widehat {BOC} = {120^0}\)

\( \Rightarrow sdcung\,BC = {120^0}\) (Số đo góc ở tâm bằng số đo cung bị chắn).

b) Ta có AD//BC nên ABCD là hình thang.

Tam giác OBC cân tại O \(\left( {OB = OC = R} \right) \Rightarrow \widehat {OBC} = \widehat {OCB} = \dfrac{{{{180}^0} - \widehat {BOC}}}{2} = \dfrac{{{{180}^0} - {{120}^0}}}{2} = {30^0}\).

Tam giác OAB và tam giác OCD vuông cân tại O.

\( \Rightarrow \widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = {45^0}\)

\(\begin{array}{l} \Rightarrow \widehat {ABC} = \widehat {OBA} + \widehat {OBD} = {45^0} + {30^0} = {75^0};\\\,\,\,\,\,\,\widehat {BCD} = \widehat {OCB} + \widehat {OCD} = {30^0} + {45^0} = {75^0}\end{array}\)

\(\widehat {ABC} = \widehat {BCD} \Rightarrow ABCD\) là hình thang cân (Hình thang có 2 góc ở đáy bằng nhau).

c) Ta có \(EB = EC\)  (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow \Delta EBC\) cân tại E.

Lại có \(\widehat {EBC} = \widehat {EBO} - \widehat {OBC} = {90^0} - {30^0} = {60^0} \Rightarrow \Delta EBC\) đều (tam giác cân có 1 góc 600 là tam giác đều).