Hướng Dẫn Cách Bấm Máy Tính đạo Hàm - ReviewEdu

Việc được sử dụng máy tính để tính những phương trình, hàm số hay các tổ hợp, chỉnh hợp là điều hết sức bình thường đối với học sinh THCS và THPT. Ngoài ra, không phải học học sinh nào cũng có lối đi đúng đắn từ khi biết đến chúng nên việc mất gốc các loại toán này cũng không phải ít. Vậy nên, bài viết dưới đây Reviewedu.net cung cấp cho bạn đọc cách bấm máy tính đạo hàm nhanh để thuận tiện trong việc học tập và làm bài tập của mình.

Danh mục bài viết

Toggle

• Đạo hàm là gì?
  • Ý nghĩa hình học
  • Ý nghĩa vật lý
  • Đạo hàm của một số hàm số cơ bản
• Các công thức đạo hàm
• Cách bấm máy tính đạo hàm

Đạo hàm là gì?

Đạo hàm là tỉ số giữa số gia của hàm số và số gia của đối số tại điểm x0. Giá trị của đạo hàm thể hiện chiều biến thiên của hàm số và độ lớn của biến thiên này. Đạo hàm có ý nghĩa hình học và vật lý.

Ý nghĩa hình học

Đạo hàm của hàm số f(x) tại điểm x0là hệ số góc của tiếp tuyến tại điểm M(x0,f(x0)) M(x0,f(x0)) đó.

=> Phương trình của tiếp tuyến tại điểm M: y−y0 = f′(x0)(x−x0)y−y0 = f′(x0)(x−x0)

Ý nghĩa vật lý

Xét chuyển động thẳng s = f(t)s = f(t)

Khi đó vận tốc tức thời tại thời điểm t0 là: v(t0) = s′(t0) = f′(t0)v(t0) = s′(t0) = f′(t0)

Còn gia tốc tức thời tại thời điểm t0 là đạo hàm cấp 2 của phương trình chuyển động:

a(t0) = f′′(t0)a(t0) = f″(t0)

Giả sử điện lượng Q truyền trong dây dẫn xác định bởi phương trình:

Q = f(t)Q = f(t)

Cường độ tức thời của dòng điện tại thời điểm t0: I(t0) = Q′(t0) = f′(t0)

Đạo hàm của một số hàm số cơ bản

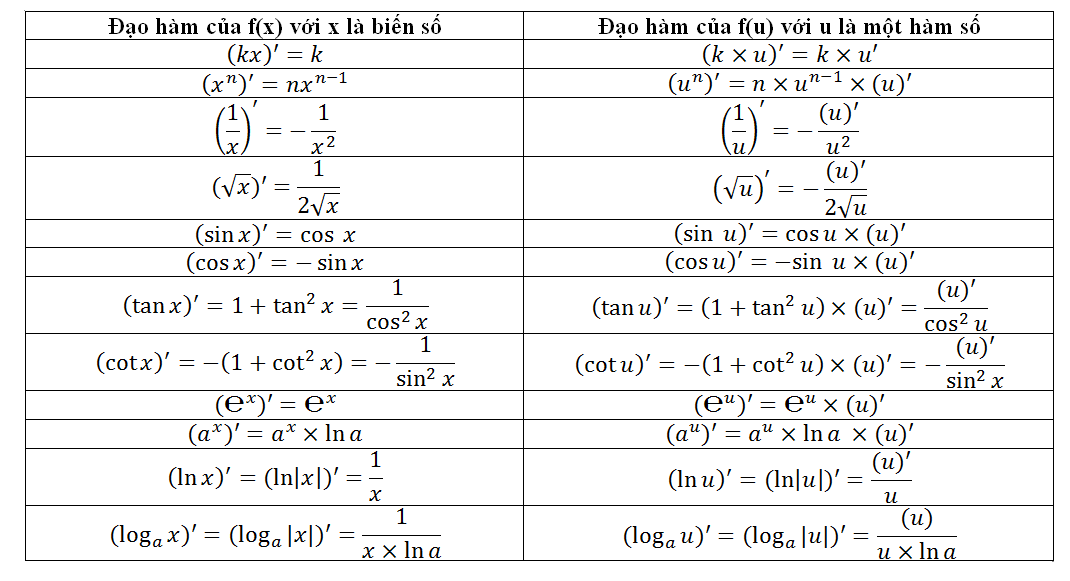Đạo hàm của một số phân thức hữu tỉ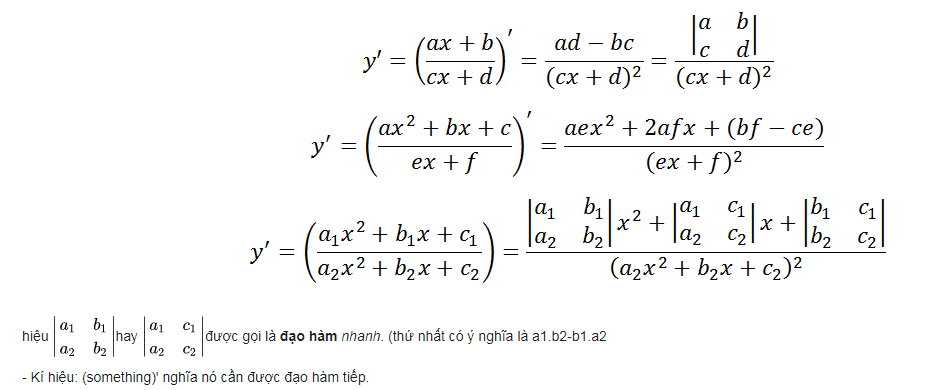 

Các công thức đạo hàm

Đạo hàm của các hàm lượng giác và các hàm lượng giác ngược.

Đạo hàm của các hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin(x), cos(x) và tan(x).

Biết được đạo hàm của sin(x) và cos(x), chúng ta dễ dàng tìm được đạo hàm của các hàm lượng giác còn lại do chúng được biểu diễn bằng hai hàm trên, bằng cách dùng quy tắc thương.

Phép chứng minh đạo hàm của sin(x) và cos(x) được diễn giải ở bên dưới, và từ đó cho phép tính đạo hàm của các hàm lượng giác khác.

Việc tính đạo hàm của hàm lượng giác ngược và một số hàm lượng giác thông dụng khác cũng được trình bày ở bên dưới.

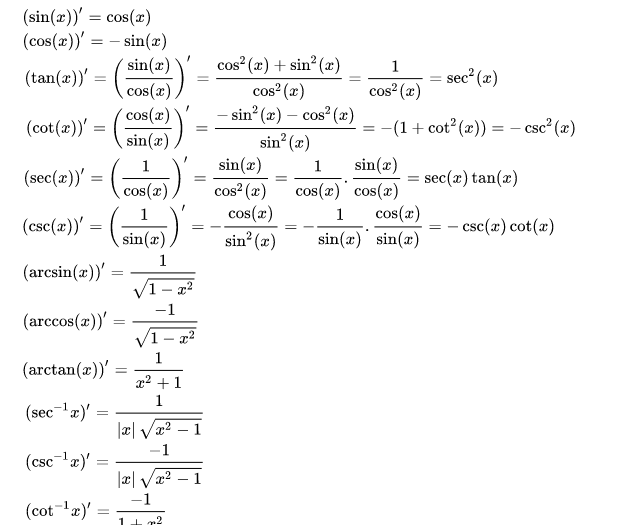
Cách bấm máy tính đạo hàm

Xem thêm:

Cách bấm máy tính nguyên hàm

Cách bấm máy tính logarit

Cách bấm máy tính chỉnh hợp

Đánh giá bài viết