I. Định Nghĩa Và Các Phép Toán Về Vectơ Trong Không Gian - SureTEST
Có thể bạn quan tâm
I. Định nghĩa và các phép toán về vectơ trong không gian
1. Định nghĩa
Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu $\overrightarrow {AB} $ chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn được kí hiệu là $\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y ,...$
2. Phép cộng và phép trừ vectơ trong không gian
* Tính chất
a) Tính chất giao hoán: $\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a $
b) Tính chất kết hợp: $\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)$
c) Tính chất của vectơ $\overrightarrow 0 $: $\overrightarrow a + \overrightarrow 0 = \overrightarrow 0 + \overrightarrow a = \overrightarrow a $
d) $\overrightarrow a + \left( { - \overrightarrow a } \right) = - \overrightarrow a + \overrightarrow a = \overrightarrow 0 $
* Các quy tắc cần nhớ khi tính toán
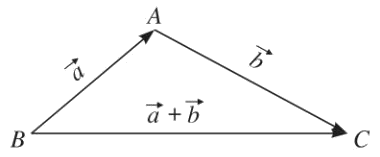
a) Quy tắc ba điểm
Với ba điểm A, B, C bất kì ta có:
$\begin{array}{l} \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \\ \overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \\ \overrightarrow {BC} = \overrightarrow {AC} + \left( { - \overrightarrow {AB} } \right) = \overrightarrow {AC} + \overrightarrow {BA} = \overrightarrow {BA} + \overrightarrow {AC} \end{array}$
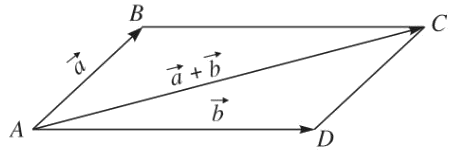
b) Quy tắc hình bình hành
Với hình bình hành ABCD ta có:
$\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} $
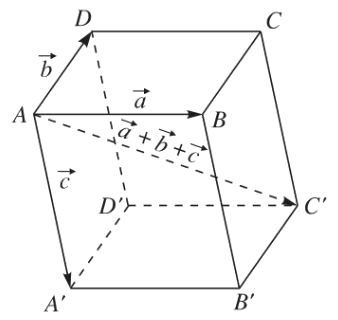
c) Quy tắc hình hộp
Cho hình hộp ABCD.A’B’C’D’ với AB, AD, AA’ là ba cạnh có chung đỉnh A và AC’ là đường chéo, ta có:
$\overrightarrow {AC} ' = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA} '$
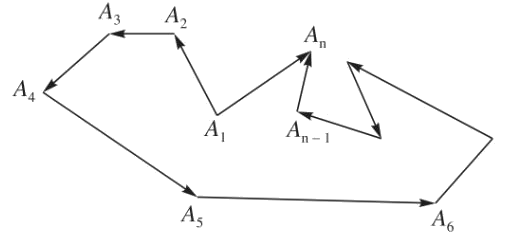
d) Mở rộng quy tắc ba điểm
Cho n điểm ${A_1},{A_2},...,{A_n}$ bất kì, ta có:
$\overrightarrow {{A_1}{A_2}} + \overrightarrow {{A_2}{A_3}} + ... + \overrightarrow {{A_{n - 1}}{A_n}} = \overrightarrow {{A_1}{A_n}} $
3. Phép nhân vectơ với một số
Trong không gian, tích của vectơ $\overrightarrow a $ với một số $k \ne 0$ là vectơ $k\overrightarrow a $ được định nghĩa tương tự như trong mặt phẳng và có các tính chất giống như các tính chất đã được xét trong mặt phẳng.
II. Điều kiện đồng phẳng của ba vectơ
1. Khái niệm về sự đồng phẳng của ba vectơ trong không gian
Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác $\overrightarrow 0 $ trong không gian. Từ một điểm O bất kì ta vẽ $\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c $. Khi đó xảy ra hai trường hợp:
* Trường hợp các đường thẳng OA, OB, OC không cùng nằm trong một mặt phẳng, ta nói ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ không đồng phẳng.
* Trường hợp các đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng, ta nói ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đồng phẳng.
2. Định nghĩa
Trong không gian, ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
3. Điều kiện để ba vectơ đồng phẳng
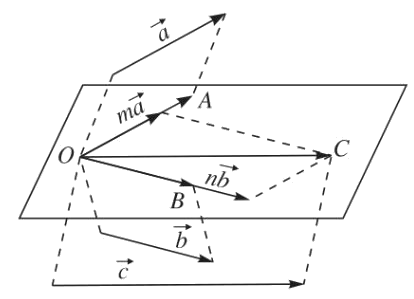
* Định lí 1
Trong không gian cho hai vectơ không cùng phương $\overrightarrow a ,\overrightarrow b $ và một vectơ $\overrightarrow c $. Khi đó ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đồng phẳng khi và chỉ khi có cặp số m, n sao cho $\overrightarrow x = m\overrightarrow a + n\overrightarrow b $. Ngoài ra, cặp số m, n là duy nhất.
* Định lí 2
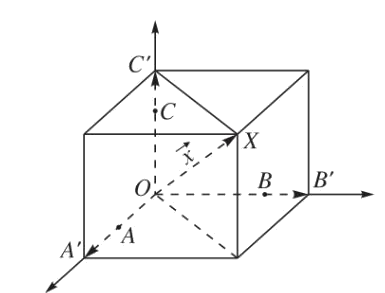
Cho $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ là ba vectơ không đồng phẳng. Với mọi vectơ $\overrightarrow x $ trong không gian ta đều tìm được một bộ ba số m, n, p sao cho $\overrightarrow x = m\overrightarrow a + n\overrightarrow b + p\overrightarrow c $. Ngoài ra, bộ ba số m, n, p là duy nhất.
Với $\overrightarrow {OX} = \overrightarrow x ,\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c $
và $\overrightarrow {OX} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} $; với $\overrightarrow {OA} ' = m\overrightarrow a ,\overrightarrow {OB} ' = n\overrightarrow b ,\overrightarrow {OC} ' = p\overrightarrow c $.
Khi đó: $\overrightarrow x = m\overrightarrow a + n\overrightarrow b + p\overrightarrow c $.
Từ khóa » Hai Vecto Song Song Trong Không Gian
-
2. Quan Hệ Song Song Trong Không Gian
-
Lý Thuyết 2 đường Thẳng Song Song Trong Không Gian
-
Vecto Trong Không Gian Là Gì? Vecto Chỉ Phương, Tích Vô Hướng, Quy ...
-
Hai đường Thẳng Song Song Trong Không Gian Khi Nào? Bài Tập Và ...
-
2 đường Thẳng Song Song Trong Không Gian Oxyz - Hỏi Đáp
-
Hai đường Thẳng Song Song - Tỷ Mỷ Làm Toán. Độc Lập Suy Nghĩ.
-
Bài 7 Trang 95 Hình 12: Cho Mặt Phẳng α đi Qua điểm M(0
-
Bài 2. Hai đường Thẳng Vuông Góc - SureTEST
-
Lý Thuyết Véc Tơ Trong Không Gian | SGK Toán Lớp 11
-
Vectơ Trong Không Gian – Bài Tập Hình Học Lớp 11
-
Phương Pháp Xác định Góc Giữa Hai đường Thẳng Trong Không Gian ...
-
Cách Chứng Minh Hai đường Thẳng Song Song Trong Không Gian
-
Cách Giải Các Dạng Toán Phương Trình đường Thẳng Trong Không Gian
-
Toán 11 Bài 2: Hai đường Thẳng Vuông Góc - VOH