Intersection Of Sets - Formula, Examples | A Intersection B - Cuemath

Intersection of Sets

The intersection of two given sets is the set that contains all the elements that are common to both sets. The symbol for the intersection of sets is "∩''. For any two sets A and B, the intersection, A ∩ B (read as A intersection B) lists all the elements that are present in both sets (common elements of A and B).

For example, if Set A = {1,2,3,4,5} and Set B = {3,4,6,8}, A ∩ B = {3,4}. Let us earn more about the properties of the intersection of sets along with examples.

1.	What is Intersection of Sets?
2.	Complement of Intersection of Sets
3.	Intersection of Sets Venn Diagram
4.	Properties of Intersection of Sets
5.	FAQs on Intersection of Sets

What is Intersection of Sets?

The intersection of sets is the set of elements which are common to the given sets. In set theory, for any two sets A and B, the intersection is defined as the set of all the elements in set A that are also present in set B. We use the symbol '∩' that denotes 'intersection of'. For example, let us represent the students who like ice creams for dessert, Brandon, Sophie, Luke, and Jess. This is set A. The students who like brownies for dessert are Ron, Sophie, Mia, and Luke. This is set B. The students who like both ice creams and brownies are Sophie and Luke. This is represented as A ∩ B.

Disjoint Sets

Two sets A and B having no elements in common are said to be disjoint, if A ∩ B = ϕ, then A and B are called disjoint sets. Example: If A = { 2, 3, 5, 9} and B = {1, 4, 6,12}, A ∩ B = { 2, 3, 5, 9} ∩ {1, 4, 6,12} = ϕ. Therefore, A and B are called disjoint sets.

Subsets

If set A is the set of natural numbers from 1 to 10 and set B is the set of odd numbers from 1 to 10, then B is the subset of A. The intersection of sets is a subset of each set forming the intersection, (A ∩ B) ⊂ A and (A ∩ B) ⊂ B.

For example- A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} , B = {2, 4, 7, 12, 14} , A ∩ B = {2, 4, 7}. Thus, A ∩ B is a subset of A, and A ∩ B is a subset of B.

A Intersection B Formula

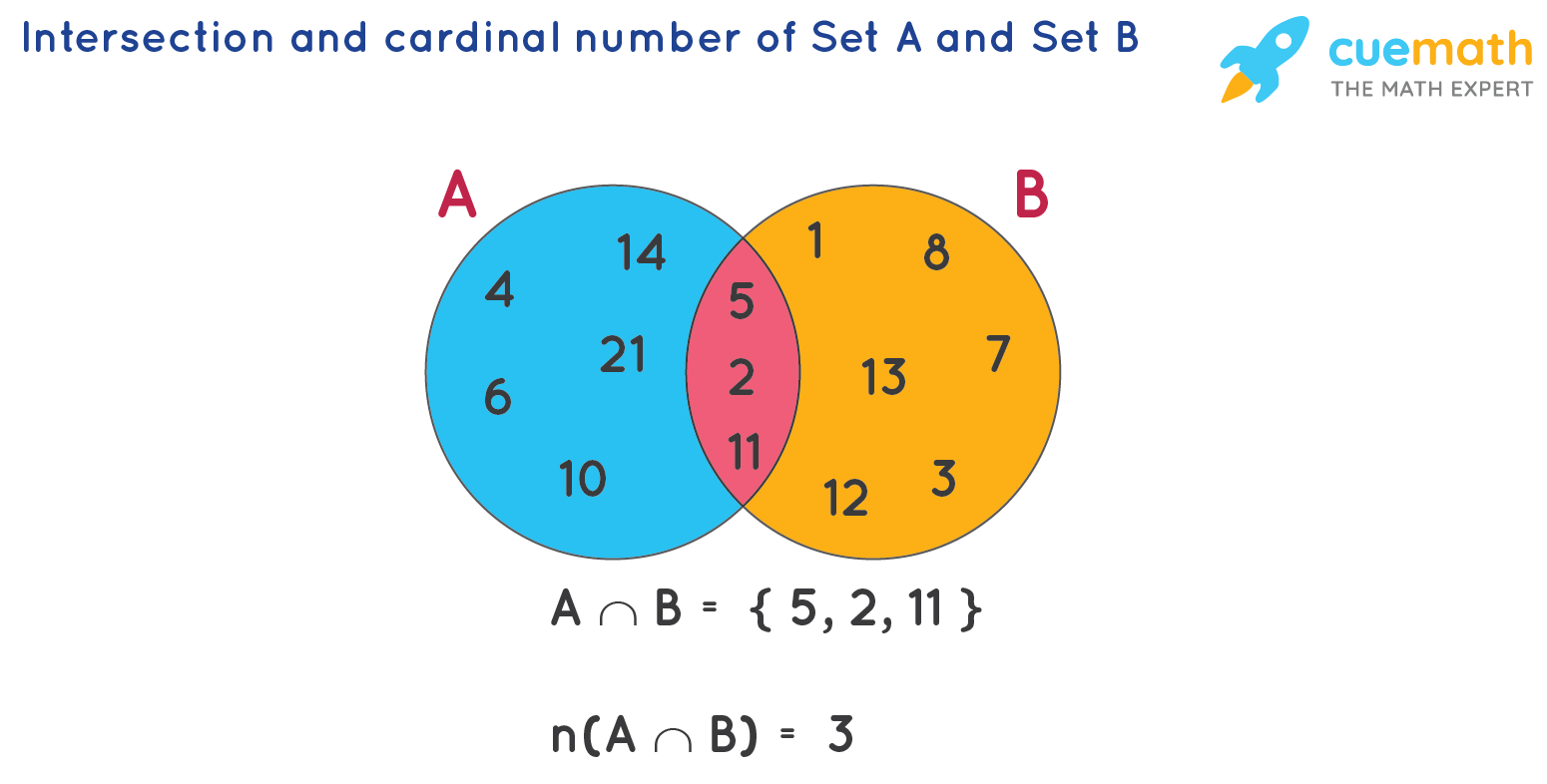
The A intersection B formula talks about the cardinality of a set. The cardinal number of a set is the total number of elements present in the set. For example, if Set A = {1,2,3,4}, then the cardinal number (represented as n (A)) = 4. Consider two sets A and B. A = {2, 4, 5, 6,10,11,14, 21}, B = {1, 2, 3, 5, 7, 8,11,12,13} and A ∩ B = {2, 5, 11}, and the cardinal number of A intersection B is represented by n(A ∩ B) = 3.

The cardinality of A ∩ B can also be found by A intersection B formula which states: n(A ∩ B)= n(A) + n(B) - n(A ∪ B). We will verify this formula for the above example, where n(A) = 8, n(B) = 9, and A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 21}. Note that n(A ∪ B) = 14 here. Then

n(A ∩ B)= n(A) + n(B) - n(A ∪ B)

3 = 8 + 9 - 14

3 = 3

Hence, n(A intersection B) formula is verified. We can observe the same in the figure below.

Complement of Intersection of Sets

The set of all the elements in the universal set but not in A ∩ B is the complement of the intersection of sets. It is denoted by (A ∩ B)' and is read as A intersection B complement. The shaded region in blue in the following Venn diagram represents (A ∩ B)'.

Example: If X = {1, 2, 3, 4, 5}, Y = {2, 4, 6, 8, 10}, and U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then X ∩ Y = {2,4} and (X ∩ Y)' = {1, 3, 5, 6, 7, 8, 9, 10}.

Intersection of Sets Venn Diagram

Intersection of sets can be easily understood using venn diagrams. Venn diagrams use circles to represent each set. Overlapping circles denote that there is some relationship between two or more sets, and that they have common elements. The circles that do not overlap do not share any common elements. The following diagram shows the intersection of sets using a Venn diagram. Here, Set A = {1, 2, 3, 4, 5} and Set B = {3, 4, 6, 8}. Therefore A ∩ B = {3 ,4}

Note: In the above figure, the portion in pink represents A ∩ B.

Properties of Intersection of Sets

Intersection of sets have properties similar to the properties of numbers. The properties of intersection of sets include the commutative law, associative law, law of null set (ϕ), universal set (U), and the idempotent law. The following table lists the properties (laws) of the intersection of sets.

Law	Rule of Intersection
Commutative Law	A ∩ B = B ∩ A
Associative Law	(A ∩ B) ∩ C = A ∩ (B ∩ C)
Law of ϕ and U	ϕ∩ A = ϕ, U ∩ A= A
Idempotent Law	A ∩ A = A
De Morgan's Law	(A ∩ B)' = A' U B'

Important Notes:

• (A ∩ B) is the set of all the elements that are common to both sets A and B.
• If A ∩ B = ϕ, then A and B are called disjoint sets.
• n(A ∩ B) = n(A) + n(B) - n(A ∪ B)

☛ Related Topics:

• Set Builder Notation
• Operations on Sets