Khối đa Diện Lồi - O2 Education
Có thể bạn quan tâm
Khối đa diện là gì? Khối đa diện lồi, đa diện đều là gì? Có tất cả bao nhiêu loại khối đa diện đều?
Xem thêm:
- Phương pháp phân chia khối đa diện
- Cách tính thể tích khối chóp nhanh nhất
- Tổng hợp 38+ tài liệu hình không gian lớp 11 hay nhất
1. Khối đa diện là gì?
Để hiểu khối đa diện là gì thì trước tiên chúng ta tìm hiểu khái niệm hình đa diện.
Hình đa diện là hình gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:
- Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
- Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Các thành phần của một hình đa diện:
- Đỉnh của các đa giác tạo nên hình đa diện được gọi là đỉnh của khối đa diện.
- Cạnh của các đa giác tạo nên hình đa diện được gọi là cạnh của khối đa diện.
- Các đa giác tạo nên hình đa diện được gọi là mặt của hình đa diện.
Hình đa diện chia không gian thành hai phần (phần bên trong và phần bên ngoài). Hình đa diện cùng với phần không gian bên trong của nó gọi là khối đa diện.
2. Khối đa diện lồi
Khối đa diện lồi là khối đa diện mà tất cả các đoạn thẳng nối hai điểm bất kỳ của nó luôn nằm hoàn toàn trong khối đa diện đó.
Công thức Euler cho khối đa diện
Với một khối đa diện (hình đa diện) bất kỳ, số đỉnh D, số mặt M và số cạnh C thì luôn có hệ thức $$D+M-C=2.$$
Ví dụ với hình lập phương ta có D = 8, M = 6, C = 12, và 8 + 6 – 12 = 2. Bạn có thể kiểm tra với một vài hình đa diện nữa để thấy công thức luôn đúng.
3. Khối đa diện đều
Khối đa diện đều là khối đa diện lồi thỏa mãn 2 tính chất như sau:
- Mỗi mặt là một đa giác đều gồm $n$ cạnh;
- Mỗi đỉnh là đỉnh chung của đúng $m$ mặt.
Khối đa diện đều đó được gọi là khối đa diện đều loại {n;m}. Người ta thấy chỉ có 5 loại khối đa diện đều như trong bảng sau:
| Loại | Tên gọi | Số đỉnh | Số cạnh | Số mặt | Số mặt phẳngđối xứng |
| {3;3} | Hình tứ diện đều | 4 | 6 | 4 | 6 |
| {4;3} | Hình lập phương | 8 | 12 | 6 | 9 |
| {3;4} | Hình bát diện đều | 6 | 12 | 8 | 9 |
| {5;3} | Hình mười hai mặt đều | 20 | 30 | 12 | 15 |
| {3;5} | Hình hai mươi mặt đều | 12 | 30 | 20 | 15 |
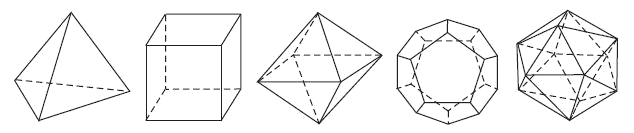

Đối với một khối đa diện đều thuộc loại {n;m}, ngoài công thức Euler $D+M-C=2$ thì còn có hệ thức sau $$p\times D=2\times C=m\times M$$
Từ khóa » Hình đa Diện Không Lồi
-
Trong Các Hình Dưới đây Hình Nào Không Phải đa Diện Lồi?
-
Trong Các Hình Dưới đây Hình Nào Không Phải đa Diện Lồi? - Hoc247
-
Câu Hỏi 1 Trang 15 SGK Hình Học 12: Tìm Ví Dụ Về Khối đa Diện Lồi Và ...
-
Nhận Diện đa Diện Lồi, đa Diện đều
-
Khối đa Diện Lồi Và Khối đa Diện đều
-
Lý Thuyết Khối đa Diện Lồi Và Khối đa Diện đều
-
Khối đa Diện Là Gì? Khái Niệm Và Tính Chất Khối đa Diện
-
Giải Bài Tập 3: Trang 26 SGK Hình Học Lớp 12 - HocTapHay
-
Trong Các Hình Dưới đây Hình Nào Không Phải đa Diện Lồi?
-
SGK Hình Học 12 - Bài 2. Khối đa Diện Lồi Và Khối đa Diện đều
-
Khối đa Diện Lồi Và Khối đa Diện đề - Tài Liệu Text - 123doc
-
Khối đa Diện Lồi Và Khối đa Diện đều
-
Mỗi Cạnh Của Hình đa Diện Là Cạnh Chung Của đúng - TopLoigiai