Khối Tâm | Vật Lý Đại Cương
Có thể bạn quan tâm
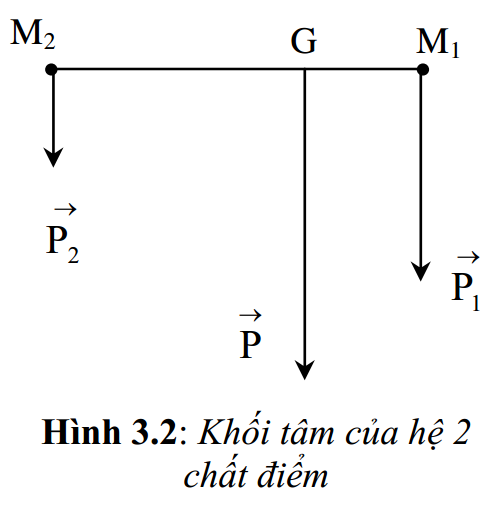
Khối được định nghĩa xuất phát từ bài toán tìm trọng tâm (điểm đặt của trọng lực) của hệ 2 chất điểm. Xét hai chất điểm M1 và M2 có khối lượng m1 và m2. Trọng lực tác dụng lên 2 chất điểm đó là \({{\overrightarrow{P}}_{1}}\) và \({{\overrightarrow{P}}_{2}}\). Hợp lực của \({{\overrightarrow{P}}_{1}}\) và \({{\overrightarrow{P}}_{2}}\) là \(\overrightarrow{P}\) có điểm đặt tại G sao cho:
\( \frac{{{M}_{1}}G}{{{M}_{2}}G}=\frac{{{P}_{2}}}{{{P}_{1}}}=\frac{{{m}_{2}}}{{{m}_{1}}} \)
\( \Rightarrow {{m}_{1}}.{{M}_{1}}G-{{m}_{2}}.{{M}_{2}}G=0 \) hay \( \Rightarrow {{m}_{1}}.\overrightarrow{{{M}_{1}}G}-{{m}_{2}}.\overrightarrow{{{M}_{2}}G}=0 \) (3.11)
Điểm G thỏa mãn (3.11) được gọi là khối tâm của hệ 2 chất điểm M1 và M2.
Trường hợp tổng quát, hệ có n chất điểm có khối lượng lần lượt là m1, m2, …, mn đặt tương ứng tại các điểm M1, M2, …, Mn, ta định nghĩa khối tâm của hệ là một điểm G thỏa mãn: \( {{m}_{1}}\overrightarrow{{{M}_{1}}G}+{{m}_{2}}\overrightarrow{{{M}_{2}}G}+…+{{m}_{n}}\overrightarrow{{{M}_{n}}G}=0 \)
Hay \( \sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{{{M}_{i}}G}}=0 \) (3.12)
Với vật rắn, khối tâm là điểm G thỏa mãn:
\( \int\limits_{\text{vật rắn }}{\overrightarrow{MG}dm}=\int\limits_{\text{vật rắn }}{\overrightarrow{MG}\rho dV}=0 \) (3.13)
Trong đó M là điểm bất kì trên vật rắn, dV là yếu tố thể tích bao quanh M (hình 3.1)
Khối tâm G được định nghĩa theo (3.12) và (3.13) là một điểm đặc trưng cho hệ, chỉ phụ thuộc vào vị trí tương đối theo (3.12) và (3.12) là một điểm đặc trưng cho hệ, chỉ phụ thuộc vào vị trí tương đối và phân bố khối lượng giữa các phần tử trong hệ, không phụ thuộc vào các yếu tố bên ngoài. Các kết quả tính toán cho thấy, nếu hệ có một yếu tố đối xứng (tâm đối xứng, trục đối xứng, mặt đối xứng) thì khối tâm của một hệ nằm trên yếu tố đối xứng đó. Như vậy, nếu hệ có nhiều yếu tố đối xứng thì khối tâm G thuộc về giao của các yếu tố đối xứng đó.
Ví dụ, khối tâm của đĩa tròn đồng chất, khối lượng phân bố đều chính là tâm của đĩa (giao điểm của hai đường kính); khối tâm của miếng sắt mỏng đồng chất, hình chữ nhật chính là giao điểm của 2 đường chéo, …
Cần phân biệt hai thuật ngữ “khối tâm” và “trọng tâm”! Trọng tâm G’ của hệ là điểm đặt của trọng lực tác dụng vào hệ, nghĩa là vị trí của G’ không phụ thuộc vào vị trí, khối lượng của các phần tử cấu tạo nên hệ mà còn phụ thuộc vào gia tốc trọng trường. Trong khi đó vị trí khối tâm G không phụ thuộc vào gia tốc trọng trường.
Trên thực tế, hầu hết kích thước các hệ vật lí mà ta khảo sát là không lớn, do đó gia tốc trọng trường hâu như không đổi tại mọi điểm và G’ trùng với G. Việc phân biệt vị trí của G’ và G là không cần thiết!
Từ khóa » Hệ Tọa độ Khối Tâm
-
[PDF] §1. Khối Tâm §2. Chuyển động Của Vật Rắn §3. Mômen Quán Tính §4 ...
-
Khối Tâm – Wikipedia Tiếng Việt
-
[PDF] VẬT LÝ ĐẠI CƯƠNG 1
-
Một Số Phương Pháp Xác định Khối Tâm Và Cách Xác định Mô Men ...
-
Chuong 3 Dong Luc Hoc He Chat Diem - SlideShare
-
Bài Giảng Vật Lý đại Cương 1 - Chương 3 Động Học Và ...
-
CƠ LÝ THUYẾT | BÀI 3. (Buổi 1) Tìm Tọa độ Khối Tâm Vật Phẳng
-
Chương 3: Cơ Học Hệ Chất điểm - Vật Rắn
-
Một Số Phương Pháp để Xác định Khối Tâm Của Vật Rắn Và Mô Men ...
-
SKKN Một Số Phương Pháp để Xác định Khối Tâm Của Vật Rắn Và Mô ...
-
Khối Tâm Của Hệ Chất điểm. Xác định Trọng Tâm Lớn
-
[PDF] VẬT LÝ ĐẠI CƯƠNG 1 (CƠ - NHIỆT) PHẦN 1
-
BÀI 6 : CHUYỂN ĐỘNG CỦA KHỐI TÂM VẬT RẮN ĐỘNG NĂNG ...