Liên Hệ Giữa Cung Và Dây: Lý Thuyết Và Các Dạng Toán Thường Gặp

Trong chương trình Toán lớp 9, các em sẽ được làm quen với liên hệ giữa cung và dây. Đây là phần kiến thức quan trọng, những dạng toán về liên hệ giữa cung và dây sẽ xuất hiện trong hầu hết các bài thi quan trọng ở các mức độ khác nhau từ dễ đến khó.

Để các em nắm được đầy đủ kiến thức về phần này, Đọc Tài Liệu đem đến tài liệu tổng hợp lý thuyết liên hệ giữa cung và dây ở bài viết dưới đây, hy vọng sẽ là một tài liệu hữu ích cho quá trình học tập của các em.

Cùng tham khảo nhé!

I. Lý thuyết liên hệ giữa cung và dây

1. Định lý 1:

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

+) Hai cung bằng nhau căng hai dây bằng nhau.

+) Hai dây bằng nhau căng hai cung bằng nhau.

Ví dụ: \(\overparen{AB} = \overparen{CD}  \Leftrightarrow AB = CD.\)

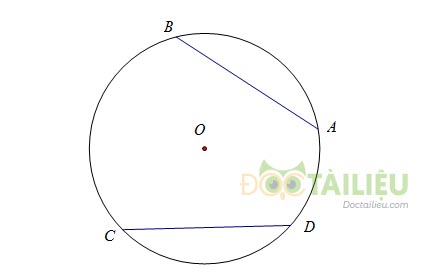
2. Định lý 2:

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

+) Cung lớn hơn căng dây lớn hơn.

+) Dây lớn hơn căng cung lớn hơn.

Ví dụ: \(\overparen{AB} > \overparen{CD}  \Leftrightarrow AB > CD.\)

Chú ý:

+) Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.

+) Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.

+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

II. Các dạng toán thường gặp về liên hệ giữa cung và dây

Dạng 1: So sánh các dây cung và so sánh các cung

Phương pháp:

Ta thường sử dụng các kiên thức:

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

+) Hai cung bằng nhau căng hai dây bằng nhau.

+) Hai dây bằng nhau căng hai cung bằng nhau.

+) Cung lớn hơn căng dây lớn hơn.

+) Dây lớn hơn căng cung lớn hơn.

Sử dụng liên hệ giữa dây và đường kính, định lý Pytago và hệ thức lượng trong tam giác vuông.

III. Bài tập về về liên hệ giữa cung và dây

Cho đường tròn (O). Gọi I là điểm chính giữa dây cung AB (Không phải là cung nửa đường tròn) và H là trung điểm của dây AB. Chứng minh rằng đường thẳng IH đi qua tâm O của đường tròn.

Lời giải:

Ta có: \(\overparen{IA}= \overparen{IB}\) (gt)

\( \Rightarrow IA = IB\) (2 cung bằng nhau căng 2 dây bằng nhau)

\( \Rightarrow\)  I  nằm trên đường trung trực của AB

OA = OB (bán kính (O))

\( \Rightarrow\) O nằm trên đường trung trực của AB

Suy ra: OI là đường trung trực của AB

H là trung điểm của AB, do đó OI đi qua trung điểm H

Vậy 3 điểm I, H, O thẳng hàng.

*****************

Hy vọng với hệ thống kiến thức lý thuyết liên hệ giữa cung và dây trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!