Longest Common Subsequence Problem - Techie Delight

The Longest Common Subsequence (LCS) problem is finding the longest subsequence present in given two sequences in the same order, i.e., find the longest sequence which can be obtained from the first original sequence by deleting some items and from the second original sequence by deleting other items.

The problem differs from the problem of finding the longest common substring. Unlike substrings, subsequences are not required to occupy consecutive positions within the original string.

For example, consider the two following sequences, X and Y:

X: ABCBDAB Y: BDCABA The length of the LCS is 4 LCS are BDAB, BCAB, and BCBA

Practice this problem

A naive solution is to check if every subsequence of X[1…m] to see if it is also a subsequence of Y[1…n]. As there are 2m subsequences possible of X, the time complexity of this solution would be O(n.2m), where m is the length of the first string and n is the length of the second string.

The LCS problem has optimal substructure. That means the problem can be broken down into smaller, simple “subproblems”, which can be broken down into yet simpler subproblems, and so on, until, finally, the solution becomes trivial.

1. Let’s consider two sequences, X and Y, of length m and n that both end in the same element.

To find their LCS, shorten each sequence by removing the last element, find the LCS of the shortened sequences, and that LCS append the removed element. So, we can say that.

LCS(X[1…m], Y[1…n]) = LCS(X[1…m-1], Y[1…n-1]) + X[m]    if X[m] = Y[n]

2. Now suppose that the two sequences does not end in the same symbol.

Then the LCS of X and Y is the longer of the two sequences LCS(X[1…m-1], Y[1…n]) and LCS(X[1…m], Y[1…n-1]). To understand this property, let’s consider the two following sequences:

X: ABCBDAB (n elements) Y: BDCABA (m elements)

The LCS of these two sequences either ends with B (the last element of the sequence X) or does not.

Case 1: If LCS ends with B, then it cannot end with A, and we can remove A from the sequence Y, and the problem reduces to LCS(X[1…m], Y[1…n-1]).

Case 2: If LCS does not end with B, then we can remove B from sequence X and the problem reduces to LCS(X[1…m-1], Y[1…n]). For example, LCS(ABCBDAB, BDCABA) = maximum (LCS(ABCBDA, BDCABA), LCS(ABCBDAB, BDCAB)) LCS(ABCBDA, BDCABA) = LCS(ABCBD, BDCAB) + A LCS(ABCBDAB, BDCAB) = LCS(ABCBDA, BDCA) + B LCS(ABCBD, BDCAB) = maximum (LCS(ABCB, BDCAB), LCS(ABCBD, BDCA)) LCS(ABCBDA, BDCA) = LCS(ABCBD, BDC) + A And so on…

The following solution in C++, Java, and Python find the length of LCS of sequences X[0…m-1] and Y[0…n-1] recursively using the LCS problem’s optimal substructure property:

C++

12345678910111213141516171819202122232425262728293031

#include <iostream>#include <string>usingnamespacestd; // Function to find the length of the longest common subsequence of// sequences `X[0…m-1]` and `Y[0…n-1]`intLCSLength(stringX,stringY,intm,intn){// return if the end of either sequence is reachedif(m==0||n==0){return0;} // if the last character of `X` and `Y` matchesif(X[m-1]==Y[n-1]){returnLCSLength(X,Y,m-1,n-1)+1;} // otherwise, if the last character of `X` and `Y` don't matchreturnmax(LCSLength(X,Y,m,n-1),LCSLength(X,Y,m-1,n));} intmain(){stringX="ABCBDAB",Y="BDCABA"; cout<<"The length of the LCS is "<<LCSLength(X,Y,X.length(),Y.length()); return0;}

Download  Run Code

Output: The length of the LCS is 4

Java

1234567891011121314151617181920212223242526272829

classMain{// Function to find the length of the longest common subsequence of// sequences `X[0…m-1]` and `Y[0…n-1]`publicstaticintLCSLength(StringX,StringY,intm,intn){// return if the end of either sequence is reachedif(m==0||n==0){return0;} // if the last character of `X` and `Y` matchesif(X.charAt(m-1)==Y.charAt(n-1)){returnLCSLength(X,Y,m-1,n-1)+1;} // otherwise, if the last character of `X` and `Y` don't matchreturnInteger.max(LCSLength(X,Y,m,n-1),LCSLength(X,Y,m-1,n));} publicstaticvoidmain(String[]args){StringX="ABCBDAB",Y="BDCABA"; System.out.println("The length of the LCS is "+LCSLength(X,Y,X.length(),Y.length()));}}

Download  Run Code

Output: The length of the LCS is 4

Python

1234567891011121314151617181920212223

# Function to find the length of the longest common subsequence of# sequences `X[0…m-1]` and `Y[0…n-1]`defLCSLength(X,Y,m,n): # return if the end of either sequence is reachedifm==0orn==0:return0 # if the last character of `X` and `Y` matchesifX[m-1]==Y[n-1]:returnLCSLength(X,Y,m-1,n-1)+1 # otherwise, if the last character of `X` and `Y` don't matchreturnmax(LCSLength(X,Y,m,n-1),LCSLength(X,Y,m-1,n)) if__name__=='__main__': X='ABCBDAB'Y='BDCABA' print('The length of the LCS is',LCSLength(X,Y,len(X),len(Y)))

Download  Run Code

Output: The length of the LCS is 4

The worst-case time complexity of the above solution is O(2(m+n)) and occupies space in the call stack, where m and n are the length of the strings X and Y. The worst case happens when there is no common subsequence present in X and Y (i.e., LCS is 0), and each recursive call will end up in two recursive calls.

The LCS problem exhibits overlapping subproblems. A problem is said to have overlapping subproblems if the recursive algorithm for the problem solves the same subproblem repeatedly rather than generating new subproblems.

Let’s consider the recursion tree for two sequences of length 6 and 8 whose LCS is 0.

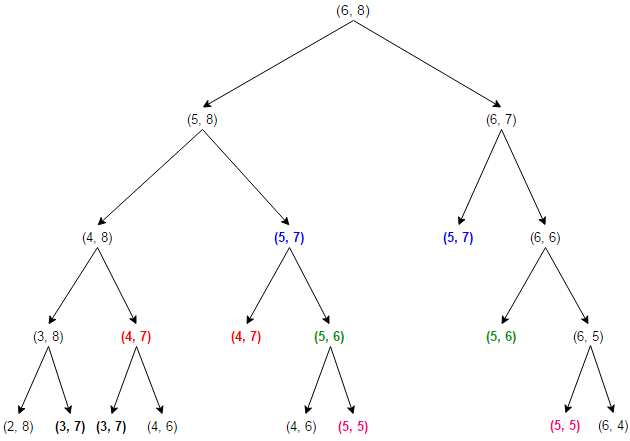
As we can see, the same subproblems (highlighted in the same color) are getting computed repeatedly. We know that problems having optimal substructure and overlapping subproblems can be solved by dynamic programming, in which subproblem solutions are memoized rather than computed repeatedly. This method is demonstrated below in C++, Java, and Python:

C++

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

#include <iostream>#include <string>#include <unordered_map>usingnamespacestd; // Function to find the length of the longest common subsequence of substring// `X[0…m-1]` and `Y[0…n-1]`intLCSLength(stringX,stringY,intm,intn,auto&lookup){// return if the end of either string is reachedif(m==0||n==0){return0;} // construct a unique map key from dynamic elements of the inputstringkey=to_string(m)+"|"+to_string(n); // if the subproblem is seen for the first time, solve it and// store its result in a mapif(lookup.find(key)==lookup.end()){// if the last character of `X` and `Y` matchesif(X[m-1]==Y[n-1]){lookup[key]=LCSLength(X,Y,m-1,n-1,lookup)+1;}else{// otherwise, if the last character of `X` and `Y` don't matchlookup[key]=max(LCSLength(X,Y,m,n-1,lookup),LCSLength(X,Y,m-1,n,lookup));}} // return the subproblem solution from the mapreturnlookup[key];} intmain(){stringX="ABCBDAB",Y="BDCABA"; // create a map to store solutions to subproblemsunordered_map<string,int>lookup; cout<<"The length of the LCS is "<<LCSLength(X,Y,X.length(),Y.length(),lookup); return0;}

Download  Run Code

Output: The length of the LCS is 4

Java

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

importjava.util.HashMap;importjava.util.Map; classMain{// Function to find the length of the longest common subsequence of substring// `X[0…m-1]` and `Y[0…n-1]`publicstaticintLCSLength(StringX,StringY,intm,intn,Map<String,Integer>lookup){// return if the end of either string is reachedif(m==0||n==0){return0;} // construct a unique map key from dynamic elements of the inputStringkey=m+"|"+n; // if the subproblem is seen for the first time, solve it and// store its result in a mapif(!lookup.containsKey(key)){// if the last character of `X` and `Y` matchesif(X.charAt(m-1)==Y.charAt(n-1)){lookup.put(key,LCSLength(X,Y,m-1,n-1,lookup)+1);}else{// otherwise, if the last character of `X` and `Y` don't matchlookup.put(key,Integer.max(LCSLength(X,Y,m,n-1,lookup),LCSLength(X,Y,m-1,n,lookup)));}} // return the subproblem solution from the mapreturnlookup.get(key);} publicstaticvoidmain(String[]args){StringX="ABCBDAB",Y="BDCABA"; // create a map to store solutions to subproblemsMap<String,Integer>lookup=newHashMap<>(); System.out.println("The length of the LCS is "+LCSLength(X,Y,X.length(),Y.length(),lookup));}}

Download  Run Code

Output: The length of the LCS is 4

Python

1234567891011121314151617181920212223242526272829303132333435363738

# Function to find the length of the longest common subsequence of substring# `X[0…m-1]` and `Y[0…n-1]`defLCSLength(X,Y,m,n,lookup): # return if the end of either string is reachedifm==0orn==0:return0 # construct a unique key from dynamic elements of the inputkey=(m,n) # if the subproblem is seen for the first time, solve it and# store its result in a dictionaryifkey notinlookup: # if the last character of `X` and `Y` matchesifX[m-1]==Y[n-1]:lookup[key]=LCSLength(X,Y,m-1,n-1,lookup)+1 else:# otherwise, if the last character of `X` and `Y` don't matchlookup[key]=max(LCSLength(X,Y,m,n-1,lookup),LCSLength(X,Y,m-1,n,lookup)) # return the subproblem solution from the dictionaryreturnlookup[key] if__name__=='__main__': X='ABCBDAB'Y='BDCABA' # create a dictionary to store solutions to subproblemslookup={} print('The length of the LCS is',LCSLength(X,Y,len(X),len(Y),lookup))

Download  Run Code

Output: The length of the LCS is 4

The time complexity of the above top-down solution is O(m.n) and requires O(m.n) extra space, where m and n are the length of the strings X and Y. Note that we can also use an array instead of a map. Check implementation here.

The above memoized version follows the top-down approach since we first break the problem into subproblems and then calculate and store values. We can also solve this problem in a bottom-up manner. In the bottom-up approach, we calculate the smaller values of LCS(i, j) first, then build larger values from them.

           | 0                                        if i == 0 or j == 0 LCS[i][j] = | LCS[i – 1][j – 1] + 1                    if X[i-1] == Y[j-1]            | longest(LCS[i – 1][j], LCS[i][j – 1])    if X[i-1] != Y[j-1]

Let X be XMJYAUZ, and Y be MZJAWXU. The longest common subsequence between X and Y is MJAU. The following table is generated by the function LCSLength(), which shows the LCS’s length between prefixes of X and Y. The i'th row and j'th column show the LCS’s length of substring X[0…i-1] and Y[0…j-1].

This is demonstrated below in C++, Java, and Python:

C++

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253

#include <iostream>#include <string>usingnamespacestd; // Function to find the length of the longest common subsequence of substring// `X[0…m-1]` and `Y[0…n-1]`intLCSLength(stringX,stringY){intm=X.length(),n=Y.length(); // lookup table stores solution to already computed subproblems;// i.e., `lookup[i][j]` stores the length of LCS of substring// `X[0…i-1]` and `Y[0…j-1]`intlookup[m+1][n+1]; // first column of the lookup table will be all 0sfor(inti=0;i<=m;i++){lookup[i][0]=0;} // first row of the lookup table will be all 0sfor(intj=0;j<=n;j++){lookup[0][j]=0;} // fill the lookup table in a bottom-up mannerfor(inti=1;i<=m;i++){for(intj=1;j<=n;j++){// if the current character of `X` and `Y` matchesif(X[i-1]==Y[j-1]){lookup[i][j]=lookup[i-1][j-1]+1;}// otherwise, if the current character of `X` and `Y` don't matchelse{lookup[i][j]=max(lookup[i-1][j],lookup[i][j-1]);}}} // LCS will be the last entry in the lookup tablereturnlookup[m][n];} intmain(){stringX="XMJYAUZ",Y="MZJAWXU"; cout<<"The length of the LCS is "<<LCSLength(X,Y); return0;}

Download  Run Code

Output: The length of the LCS is 4

Java

12345678910111213141516171819202122232425262728293031323334353637383940

classMain{// Function to find the length of the longest common subsequence of substring// `X[0…m-1]` and `Y[0…n-1]`publicstaticintLCSLength(StringX,StringY){intm=X.length(),n=Y.length(); // lookup table stores solution to already computed subproblems,// i.e., `T[i][j]` stores the length of LCS of substring// `X[0…i-1]` and `Y[0…j-1]`int[][]T=newint[m+1][n+1]; // fill the lookup table in a bottom-up mannerfor(inti=1;i<=m;i++){for(intj=1;j<=n;j++){// if the current character of `X` and `Y` matchesif(X.charAt(i-1)==Y.charAt(j-1)){T[i][j]=T[i-1][j-1]+1;}// otherwise, if the current character of `X` and `Y` don't matchelse{T[i][j]=Integer.max(T[i-1][j],T[i][j-1]);}}} // LCS will be the last entry in the lookup tablereturnT[m][n];} publicstaticvoidmain(String[]args){StringX="XMJYAUZ",Y="MZJAWXU"; System.out.println("The length of the LCS is "+LCSLength(X,Y));}}

Download  Run Code

Output: The length of the LCS is 4

Python

123456789101112131415161718192021222324252627282930313233

# Function to find the length of the longest common subsequence of substring# `X[0…m-1]` and `Y[0…n-1]`defLCSLength(X,Y): m=len(X)n=len(Y) # lookup table stores solution to already computed subproblems;# i.e., `T[i][j]` stores the length of LCS of substring# `X[0…i-1]` and `Y[0…j-1]`T=[[0forxinrange(n+1)]foryinrange(m+1)] # fill the lookup table in a bottom-up mannerforiinrange(1,m+1):forjinrange(1,n+1):# if the current character of `X` and `Y` matchesifX[i-1]==Y[j-1]:T[i][j]=T[i-1][j-1]+1# otherwise, if the current character of `X` and `Y` don't matchelse:T[i][j]=max(T[i-1][j],T[i][j-1]) # LCS will be the last entry in the lookup tablereturnT[m][n] if__name__=='__main__': X='XMJYAUZ'Y='MZJAWXU' print('The length of the LCS is',LCSLength(X,Y))

Download  Run Code

Output: The length of the LCS is 4

The time complexity of the above bottom-up solution is O(m.n) and requires O(m.n) extra space, where m and n are the length of the strings X and Y. The space complexity of the above solution can be improved to O(n) as calculating LCS of a row of the LCS table requires only the solutions to the current row and the previous row.

Applications of LCS problem

The longest common subsequence problem forms the basis of data comparison programs such as the diff utility and use in the field of bioinformatics. It is also widely used by revision control systems such as Git.

Also See:

Longest Common Subsequence of k–sequences

Longest Common Subsequence (LCS) | Space optimized version

Longest Common Subsequence | Finding all LCS

References: https://en.wikipedia.org/wiki/Longest_common_subsequence_problem