Lực Lorentz – Wikipedia Tiếng Việt
Có thể bạn quan tâm
| Bài viết về |
| Điện từ học |
|---|
 |
|
Tĩnh điện
|
Tĩnh từ
|
Điện động
|
Mạch điện
|
Phát biểu hiệp phương saiTenxơ điện từ(tenxơ ứng suất–năng lượng)
|
Các nhà khoa học
|
|
Trong vật lý học và điện từ học, lực Lorentz là lực tổng hợp của lực điện và lực từ tác dụng lên một điện tích điểm chuyển động trong trường điện từ.
Định luật phát biểu rằng nếu hạt có điện tích q (C) chuyển động với vận tốc v (m/s) trong điện trường E (V/m) và từ trường B (T) thì nó sẽ chịu lực tác dụng lên nó. Định luật III Newton phát biểu về lực và phản lực, do vậy mặc dù phản lực của từ trường là nhỏ nhưng nó phải được tính đến. Lực Lorentz bằng:
Các công thức phát sinh từ công thức cơ bản này miêu tả lực từ tác dụng lên dây dẫn có dòng điện chạy qua (đôi khi gọi là lực Laplace), lực điện từ trong một vòng dây di chuyển qua từ trường (một khía cạnh của định luật cảm ứng điện từ Faraday), và lực tác dụng lên điện tích điểm chuyển động với vận tốc gần bằng tốc độ ánh sáng (dạng tương đối tính của lực Lorentz).
Oliver Heaviside là người đầu tiên suy luận ra công thức cho lực Lorentz vào năm 1889,[1] mặc dù một số nhà lịch sử cho rằng James Clerk Maxwell đã đưa ra nó trong một bài báo năm 1865.[2] Định luật được đặt theo tên của Hendrik Lorentz, người tìm ra công thức sau Heaviside một vài năm và ông đã nghiên cứu và giải thích chi tiết ý nghĩa của lực này.
Lực từ động
[sửa | sửa mã nguồn]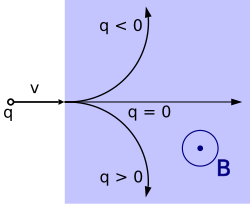
Thành phần gây ra bởi từ trường của lực này, còn gọi là lực từ hay đôi khi là lực Lorentz, có phương luôn vuông góc với phương chuyển động của hạt mang điện và làm thay đổi quỹ đạo chuyển động của hạt mang điện. Nếu hạt mang điện chuyển động theo phương vuông góc với đường cảm ứng từ thì hạt sẽ chuyển động theo quỹ đạo tròn, nếu hạt chuyển động theo phương không vuông góc với đường cảm ứng từ thì quỹ đạo của nó sẽ là hình xoắn ốc.
Lực tác động của từ trường lên dòng điện có nguyên nhân là thành phần này của lực Lorentz.
Lực từ giữa các cực của nam châm, cũng là tổng hợp lực gây ra bởi từ trường của nam châm này lên các electron chuyển động quanh nguyên tử ở nam châm kia, về bản chất cũng là thành phần này của lực Lorentz:
Xem thêm
[sửa | sửa mã nguồn]- Lực
- Hiệu ứng Hall
- Điện từ học
- Hấp dẫn từ học
- Định luật Ampère
- Hendrik Lorentz
- Phương trình Maxwell
- Phương trình Maxwell trong thuyết tương đối hẹp
Tham khảo
[sửa | sửa mã nguồn]- ^ Oliver Heaviside By Paul J. Nahin, p120
- ^ Huray, Paul G. (2009). Maxwell's Equations. Wiley-IEEE. tr. 22. ISBN 0-470-54276-4.
Danh mục tham khảo
[sửa | sửa mã nguồn]- Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
- Griffiths, David J. (1999). Introduction to electrodynamics (ấn bản thứ 3). Upper Saddle River, [NJ.]: Prentice-Hall. ISBN 0-13-805326-X.
- Jackson, John David (1999). Classical electrodynamics (ấn bản thứ 3). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
- Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.{{Chú thích sách}}: Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- Srednicki, Mark A. (2007). Quantum field theory. Cambridge, [England]; New York [NY.]: Cambridge University Press. ISBN 978-0-521-86449-7.
Liên kết ngoài
[sửa | sửa mã nguồn]- Interactive Java tutorial on the Lorentz force Lưu trữ ngày 10 tháng 4 năm 2010 tại Wayback Machine National High Magnetic Field Laboratory
- Faraday's law: Tankersley and Mosca Lưu trữ ngày 26 tháng 2 năm 2009 tại Wayback Machine
- Notes from Physics and Astronomy HyperPhysics at Georgia State University; see also home page
- Interactive Java applet on the magnetic deflection of a particle beam in a homogeneous magnetic field Lưu trữ ngày 13 tháng 8 năm 2011 tại Wayback Machine by Wolfgang Bauer
Bài viết về chủ đề vật lý này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn. |
- x
- t
- s
Từ khóa » đâu Là ứng Dụng Của Lực Lorenxo
-
Hãy Kể Vài ứng Dụng Của Lực Lo-ren-xơ? - Vật Lý Lớp 12 - Lazi
-
[CHUẨN NHẤT] Lực Lorenxơ Dùng để Làm Gì - Top Lời Giải
-
Kể Tên Vài ứng Dụng Của Lực Lorenxo Câu Hỏi 3919837
-
Đâu Là ứng Dụng Của Lực Lorenxo? A. La Bàn. B. Khối Phổ Kế. C ...
-
Ứng Dụng Của Lực Lorentz - Tài Liệu Text - 123doc
-
Lực Lorenxơ Là Gì? Phương Của Lực Lorenxo Là Gì? Công Thức & ứng ...
-
Lực Lorentz. Nguyên Lý Chung Của Thiết Bị
-
Lý Thuyết Lực Lo-Ren-Xơ | SGK Vật Lí Lớp 11
-
Lực Lo -ren -xơ, Trắc Nghiệm Vật Lý Lớp 11 - Baitap123
-
Trong Máy Thu Hình Lực Lorenxơ được ứng Dụng để
-
Công Thức Tính Lực Lorenxơ Hay Nhất - Vật Lí Lớp 11
-
23 Câu Trắc Nghiệm Lực Lo-ren-xơ Có đáp án Chi Tiết | Vật Lí Lớp 11
-
Lực Lo-ren-xơ Là Gì? Viết Công Thức Của Lực Lo-ren-xơ. - Tech12h
-
TOP 40 Câu Trắc Nghiệm Lực Lo-ren-xơ (có đáp án 2022) – Vật Lí 11
-
Chọn Các Câu Dụng ứng Dụng Của Lực Lorentz Trong Các Lĩnh Vực ...
-
Chuyên đề Lực Lorenxơ, Chuyển động Của điện Tích Trong Từ Trường
-
Ứng Dụng Định Luật Cảm Ứng Điện Từ Vào Đời Sống - Kiến Guru
