LUYỆN TẬP HÌNH BÌNH HÀNH

LUYỆN TẬP HÌNH BÌNH HÀNH

Câu 1: Các tứ giác ABCD, EFGH & hình vẽ bên dưới có phải là hình bình hành hay không?

Lời giải:

 

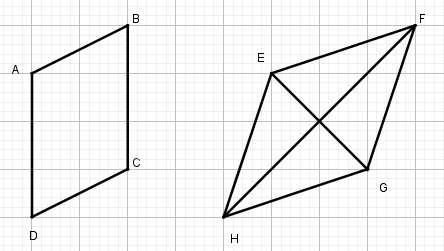
Tứ giác ABCD là hình bình hành vì có cạnh đối AD // BC và AD = BC bằng 3 cạnh ô vuông.

Tứ giác EFGH là hình bình hành vì có các cạnh đối bằng nhau.

EH = FG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông

Câu 2: Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng: DE = BF

Lời giải:

 

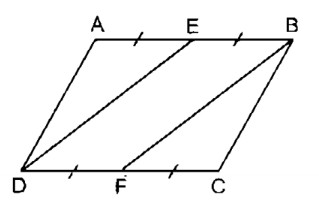
Ta có: AB = CD (tính chất hình bình hành)

EB = 1/2 AB (gt)

FD = 1/2 CD (gt)

Suy ra: EB = FD (1)

Mà AB // CD (gt)

⇒ BE // FD (2)

Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ DE = BF (tính chất hình bình hành)

Câu 3: Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.

Lời giải:

 

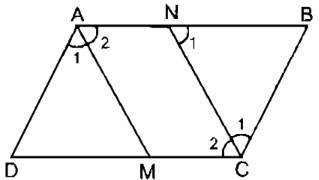
Ta có: ∠A = ∠C (tính chất hình bình hành)

∠A2 = 12 ∠A (gt)

∠C2 = 12 ∠C (gt)

Suy ra: ∠A2 = ∠C2 (gt)

AB // CD (gt)

Hay AN // CM (1)

Mà ∠N1 = ∠C2(so le trong)

Suy ra: ∠A2= ∠N1

AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)

Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.

Câu 4: Hình bên cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.

Lời giải:

 

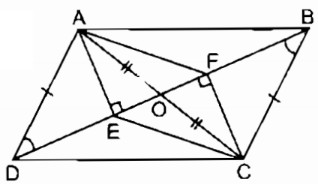
Gọi O là'giao điểm của AC và BD, ta có:

OA = OC (tính chất hình bình hành) (1)

Xét hai tam giác vuông AEO và CFO, ta có:

∠(AEO) = ∠(CFO) = 90o

OA = OC (chứng minh trên)

∠(AOE) = ∠(COF) (đối đỉnh)

Do đó ΔAEO = ΔCFO (cạnh huyền, góc nhọn)

⇒ OE = OF' (2)

Từ (1) và (2) suy ra tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Câu 5: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

 

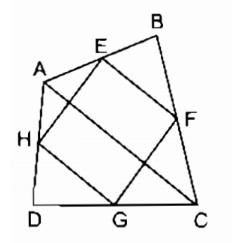
Nối đường chéo AC.

Trong ΔABC ta có:

E là trung điểm của AB (gt)

F là trung điểm của BC (gt)

Nên EF là đường trung bình của ΔABC

⇒EF//AC và EF = 1/2 AC

(tính chất đường trung hình tam giác) (1)

Trong ΔADC ta có:

H là trung điểm của AD (gt)

G là trung điểm của DC (gt)

Nên HG là đường trung bình của ΔADC

⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

Câu 6: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB, Đường chéo BD cắt AI, UK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB

Lời giải:

 

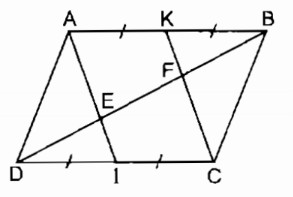
Ta có: AB = CD (tính chất hình bình hành)

AK = 1/2 AB (gt)

CI = 1/2 CD (gt)

Suy ra: AK = CI (1)

Mặt khác: AB // CD (gt)

⇒ AK // CI (2)

Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

⇒ AI // CK

Trong ΔABE, ta có:

K là trung điểm của AB (gt)

AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác)

Trong ΔDCF, ta có:

I là trung điểm của DC (gt)

AI // CK hay IE // CF nên DE = EF (tính chất đường trung bình tam giác)

Suy ra: DE = EF = FB

Câu 7: Tính các góc của hình bình hành ABCD biết:

1. ∠A = 110o
2. ∠A - ∠B = 20o

Lời giải:

a, Tứ giác ABCD là hình bình hành.

⇒ ∠C = ∠A = 110o (tính chất hình bình hành)

∠A + ∠B = 180o (2 góc trong cùng phía bù nhau)

⇒ ∠B = 180o – 110o = 70o

∠D = ∠B = 70o (tính chất hình bình hành)

b, Tứ giác ABCD là hình bình hành.

⇒∠A + ∠B = 180o (2 góc trong cùng phía bù nhau)

∠A - ∠B = 20o (gt)

Suy ra: 2∠A = 200o ⇒ ∠A = 100o

∠C = ∠A = 100o (tính chất hình bình hành)

∠A = ∠A – 20o = 100o – 20o = 80o

∠D = ∠B = 80o (tính chất hình bình hành)

Câu 8: Trong các tứ giác ở hình dưới đây, hình nào là hình bình hành.

Lời giải:

 

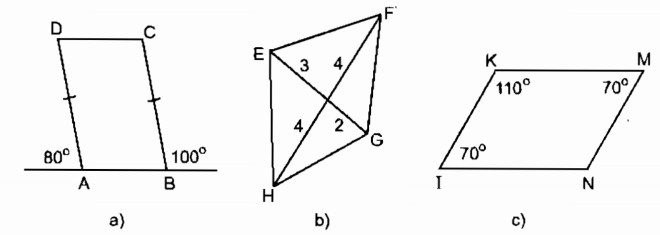
* Tứ giác ABCD là hình bình hành vì AB // CD và AB = CD.

* Tứ giác IKMN là hình bình hành vì có ∠I = ∠M = 70o và ∠K = ∠N = 110o

Câu 9: Chu vì hình bình hành ABCD bằng l0cm, chu vi tam giác ABD bằng 9cm. Tính độ dài BD.

Lời giải:

 

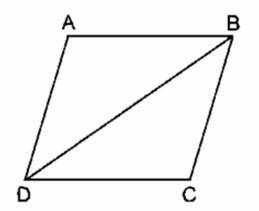
Chu vì hình bình hành ABCD bằng 10cm nên (AB + CD).2 = 10(cm)

⇒ AB + AD = 102 = 5(cm)

Chu vi của ΔABD bằng:

AB + AD + BD = 9(cm)

⇒ BD = 9 - (AB + AD) = 9 - 5 = 4(cm)

Câu 10: Hình bên dưới, cho ABCD là hình bình hành. Chứng minh rằng AE //CF.

Lời giải:

 

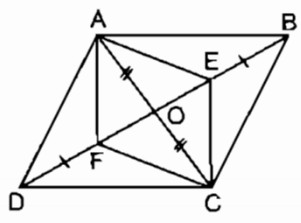
Gọi O là giao điểm của AC và BD, ta có:

OA = OC (tính chất hình bình hành)

OB = OD

Xét ΔAEB và ΔCFD, ta có:

AB = CD (tính chất hình bình hành)

∠(ABE) = ∠(CDF) (so le trong)

BE = DF (gt)

Do đó: ΔAEB = ΔCFD (c.g.c) ⇒ BE = DF

Tacó: OB = OE + BE

OD = OF + BF

Suy ra: OE = OF

Suy ra tứ giác AECF là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // CF.

Câu 11: Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng:

a, EMNF là hình bình hành

b, Các đường thẳng AC, EF, MN đồng quy.

Lời giải:

 

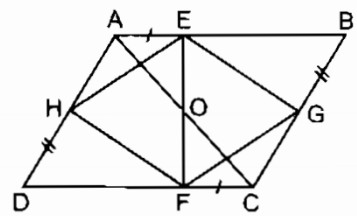
a, Xét tứ giác AECF, ta có:

AB // CD (gt)

Hay AE //CF

AE = 1/2 AB

AB = CD (tính chất hình bình hành)

Suy ra: AE = CF

Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối diện song song và bằng nhau) ⇒ AF //CE hay EN // FM (1)

Xét tứ giác BFDE ta có:

AB // CD (gt) hay BE // DF

BE = 1/2 AB (gt)

DF = 1/2 CD (gt)

AB = CD (tính chất hình bình hành)

Suy ra: BE = DF

Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMNF là hình bình hành (theo định nghĩa hình bình hành).

b, Gọi O là giao điểm của AC và EF

Tứ giác AECF là hình bình hành ⇒ OE = OF

Tứ giác EMFN là hình bình hành trên hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Suy ra: MN đi qua trung điểm O của EF.

Vậy AC, EF, MN đồng quy tại O.