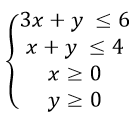Lý Thuyết Bất Phương Trình Bậc Nhất Hai ẩn Hay, Chi Tiết

I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là

ax + by ≤ c (1)

(ax + by < c; ax + by ≥ c; ax + by > c)

trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.

II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (1) được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình ax + by ≤ c như sau (tương tự cho bất phương trình ax + by ≥ c)

Bước 1. Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng Δ: ax + by = c.

Bước 2. Lấy một điểm Mo(xo; yo) không thuộc Δ (ta thường lấy gốc tọa độ )

Bước 3. Tính axo + byo và so sánh axo + byo với c.

Bước 4. Kết luận

Nếu axo + byo < c thì nửa mặt phẳng bờ Δ chứa M0 là miền nghiệm của axo + byo ≤ c

Nếu axo + byo > c thì nửa mặt phẳng bờ Δ không chứa M0 là miền nghiệm của axo + byo ≤ c

Chú ý:

Miền nghiệm của bất phương trình axo + byo ≤ c bỏ đi đường thẳng ax + by = c là miền nghiệm của bất phương trình axo + byo < c

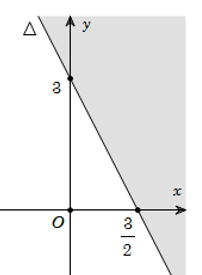
Ví dụ. Biểu diễn hình học tập nghiệm của bất phương trình 2x + y ≤ 3

Giải

Vẽ đường thẳng Δ: 2x + y = 3

Lấy gốc tọa độ O(0;0) ta thấy O ∉ Δ và có 2.0 + 0 < 3 nên nửa mặt phẳng bờ Δ chứa gốc tọa độ O là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình).

III – HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Tương tự hệ bất phương trình một ẩn

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x, y mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

Ví dụ 2. Biểu diễn hình học tập nghiệm của hệ bất phương trình

Giải.

Vẽ các đường thẳng

d1: 3x + y = 6

d2: x + y = 4

d3: x = 0 (Oy)

d4: y = 0 (Ox)

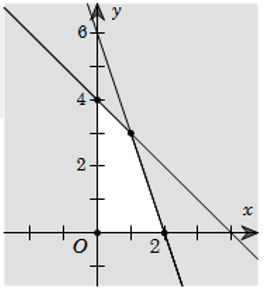
Vì điểm Mo (1;1) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tô đậm các nửa mặt phẳng bờ (d1), (d2), (d3), (d4) không chứa điểm M0. Miền không bị tô đậm (hình tứ giác OCIA kể cả bốn cạnh AI, IC, CO, OA trong hình vẽ là miền nghiệm của hệ đã cho.

IV. ÁP DỤNG VÀO BÀI TOÁN KINH TẾ

Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính.