Xác định Miền Nghiệm Của Bất Phương Trình Và Hệ Bất ... - Sách Toán

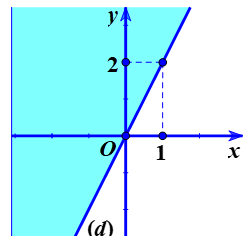
Dạng toán 1. Xác định miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn.

Ví dụ 1 . Xác định miền nghiệm của các bất phương trình sau: a) $2x-y\ge 0.$ b) $\frac{x-2y}{2}>\frac{2x+y+1}{3}.$

a) Trong mặt phẳng tọa độ, vẽ đường thẳng $\left( d \right):\text{ 2}x-y=0$, ta có $\left( d \right)$ chia mặt phẳng thành hai nửa mặt phẳng. Chọn một điểm bất kì không thuộc đường thẳng đó, chẳng hạn điểm$M\left( 1;0 \right)$, ta thấy $(1; 0)$ là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa bờ $(d)$ và chứa điểm $M\left( 1;0 \right)$ (miền không được tô màu trên hình vẽ).

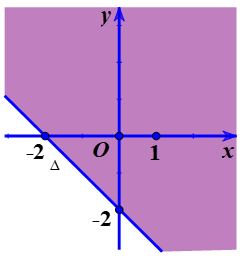
b) Ta có $\frac{x-2y}{2}>\frac{2x-y+1}{3}$ $\Leftrightarrow 3\left( x-2y \right)-2\left( 2x-y+1 \right)>0$ $\Leftrightarrow -x-4y-2>0$ $\Leftrightarrow x+4y+2<0.$ Trong mặt phẳng tọa độ, vẽ đường thẳng $\Delta :x+4y+2=0.$ Xét điểm $\text{O}\left( 0;0 \right)$, ta thấy $\left( 0;0 \right)$ không phải là nghiệm của bất phương trình đã cho do đó miền nghiệm cần tìm là nửa mặt phẳng bờ $\Delta $ (không kể đường thẳng $\Delta $) và không chứa điểm $\text{O}\left( 0;0 \right)$ (miền không được tô màu trên hình vẽ).

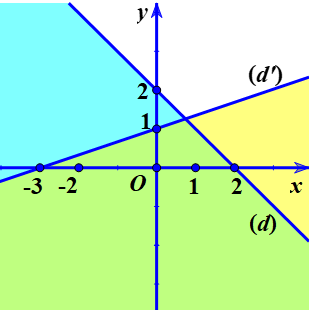
Ví dụ 2 . Xác định miền nghiệm của các hệ bất phương trình sau: a) $\left\{ \begin{matrix} x+y-2\ge 0 \\ x-3y+3\le 0 \\ \end{matrix} \right.$ b) $\left\{ \begin{align} & x+y>0 \\ & 2x-3y+6>0 \\ & x-2y+1\ge 0 \\ \end{align} \right.$

a) Vẽ các đường thẳng $\left( d \right):x+y-2=0$, $\left( d’ \right):x-3y+3=0$ trên mặt phẳng tọa độ $Oxy.$ Xét điểm $\text{O}\left( 0;0 \right)$, thấy $\left( 0;0 \right)$ không phải là nghiệm của bất phương trình $x+y-2\ge 0$ và $x-3y+3\le 0.$ Do đó miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả hai đường thẳng $\left( d \right)$ và $\left( d’ \right).$

b) Vẽ các đường thẳng $\left( d \right):x+y=0$, $\left( d’ \right):2x-3y+6=0$ và $\left( d” \right):x-2y+1=0$ trên mặt phẳng tọa độ $Oxy.$ Xét điểm $\text{O}\left( 0;0 \right)$, thấy $\left( 0;0 \right)$ là nghiệm của bất phương trình $2x-3y+6>0$ và $x-2y+1\ge 0.$ Do đó $\text{O}\left( 0;0 \right)$ thuộc miền nghiệm của bất phương trình $2x-3y+6>0$ và $x-2y+1\ge 0.$ Xét điểm $M\left( 1;0 \right)$ ta thấy $\left( 1;0 \right)$ là nghiệm của bất phương trình $x+y>0$ do đó điểm $M\left( 1;0 \right)$ thuộc miền nghiệm bất phương trình $x+y>0.$ Vậy miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả đường thẳng $\left( d” \right).$

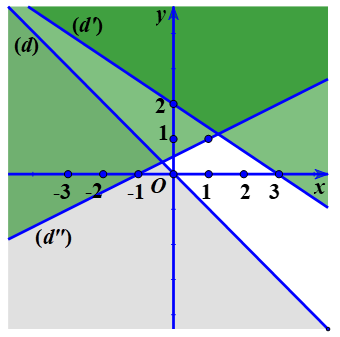
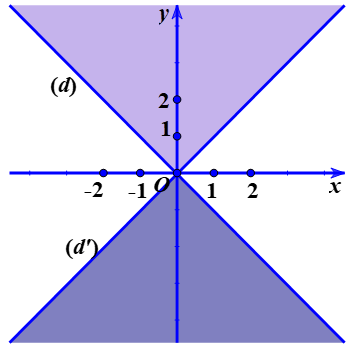
Ví dụ 3 . Xác định miền nghiệm bất phương trình $\left( x-y \right)\left( {{x}^{3}}+{{y}^{3}} \right)\ge 0.$

Ta có $\left( x-y \right)\left( {{x}^{3}}+{{y}^{3}} \right)\ge 0$ $\Leftrightarrow \left( x-y \right)\left( x+y \right)\left( {{x}^{2}}-xy+{{y}^{2}} \right)\ge 0$ $\Leftrightarrow \left( x-y \right)\left( x+y \right)\ge 0$ $\Leftrightarrow \left\{ \begin{matrix} x-y\ge 0 \\ x+y\ge 0 \\ \end{matrix} \right.$ $(1)$ hoặc $\left\{ \begin{matrix} x-y\le 0 \\ x+y\le 0 \\ \end{matrix} \right.$ $(2).$ Như vậy miền nghiệm của bất phương trình đã cho là gồm hai miền nghiệm của hệ bất phương trình $(1)$ và $(2).$ Vẽ các đường thẳng $\left( d \right):x+y=0$, $\left( d’ \right):x-y=0$ trên mặt phẳng tọa độ $Oxy.$ Xét điểm $M\left( 1;0 \right)$, ta có $\left( 1;0 \right)$ là nghiệm của các bất phương trình của hệ $(1)$ do đó $M\left( 1;0 \right)$ thuộc miền nghiệm của hệ bất phương trình $(1).$ Xét điểm $N\left( -1;0 \right)$, ta có $\left( -1;0 \right)$ là nghiệm của các bất phương trình của hệ $(2)$ do đó $N\left( -1;0 \right)$ thuộc miền nghiệm của hệ bất phương trình $(2).$ Vậy miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả hai đường thẳng $\left( d \right)$, $\left( d’ \right).$