Lý Thuyết Cực Trị Của Hàm Số & Giải Bài Tập Trong Sgk | Toán 12

Cực trị của hàm số & giải bài tập trong SGK Toán 12 bài 2: Nội dung bài học sẽ giúp các bạn nắm được hai khái niệm quan trọng là cực đại và cực tiểu, cùng với đó là điều kiện cần và đủ để hàm số có cực trị.

Tham khảo thêm:

TOPUNI 2025 - GIẢI PHÁP LUYỆN THI ĐẠI HỌC TOÀN DIỆN Đồng hành cùng 2K7 chắc vé Đại học TOP

• Bất chấp biến động thi cử, lộ trình toàn diện cho mọi kỳ thi
• Hệ thống trọn gói đầy đủ kiến thức theo sơ đồ tư duy, dễ dàng ôn luyện
• Đội ngũ giáo viên luyện thi nổi tiếng với 17+ năm kinh nghiệm
• Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình ôn luyện

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này! HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY

• Sự đồng biến nghịch biến của hàm số
• Tìm giá trị lớn nhất nhỏ nhất của hàm số
• Các dạng toán về cực trị có tham số đối với các hàm số đơn giản

A: Lý thuyết cực trị của hàm số

Cho hàm số y = f(x) liên tục trên khoảng (a ; b) và điểm x ∈ (a ; b).

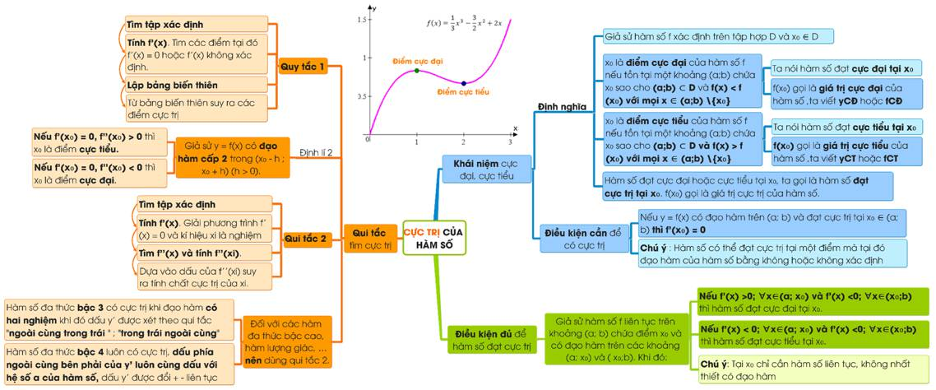
1, Định nghĩa về cực trị của hàm số

*Chú ý:

a) Cần phân biệt các các khái niệm dưới đây:

– Điểm cực trị X0 của hàm số.

– Giá trị cực trị của hàm số.

-Các điểm cực trị (x0;y0) của đồ thị hàm số.

b) Nếu y=f(x)  mà có đạo hàm trên (a;b) và đạt cực trị tại x0∈(a;b) thì f′(x0)=0

2, Điều kiện đủ để hàm số có cực trị

Hàm số có thể đạt cực trị tại những điểm mà tại đó đạo hàm của hàm số không xác định.

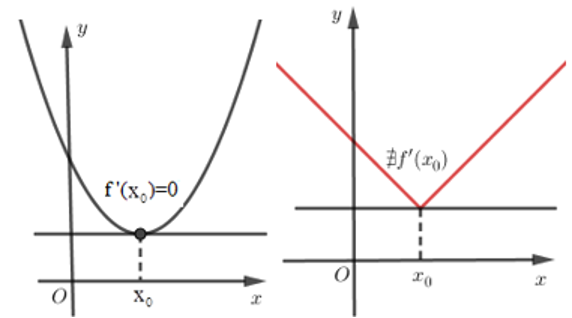
Định lý 2:

3. Quy tắc tìm cực trị của hàm số

Phương pháp làm bài:

Có thể tìm cực trị của hàm số bởi một trong hai quy tắc sau đây:

Quy tắc 1: (được suy ra từ định lý 1)

– Bước 1: Tìm tập xác định( TXD) của hàm số.

– Bước 2: Tính f′(x) tìm các điểm tại đó mà f′(x)=0 hoặc không xác định.

– Bước 3: Lập bảng biến thiên và đưa ra kết luận.

• Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó chính là điểm cực tiểu của hàm số.
• Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó chính là điểm cực đại của hàm số.

Quy tắc 2: (được suy ra từ định lý 2)

– Bước 1: Tìm tập xác định (TXD) của hàm số.

– Bước 2: Tính f′(x),giải phương trình f′(x)=0 và kí hiệu X1,…,Xn chính là các nghiệm của nó.

– Bước 3: Tính f”(x)và f”(xi).

– Bước 4: Dựa và dấu của f”(xi) từ đó suy ra các điểm cực đại và cực tiểu:

• Tại các điểm xi mà f”(xi)>0 thì đó chính là điểm cực tiểu của hàm số.
• Tại các điểm xi mà f”(xi)<0 thì đó chính là điểm cực đại của hàm số.

B: Trả lời câu hỏi và giải bài tập trong SGK Toán 12 bài 2

Trả lời câu hỏi 1 trang 13 SGK Giải tích 12 tập 1:

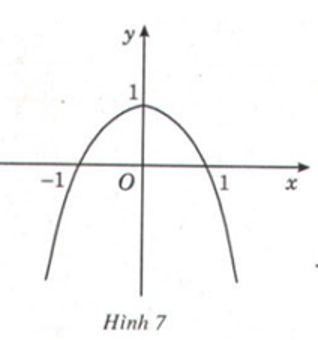
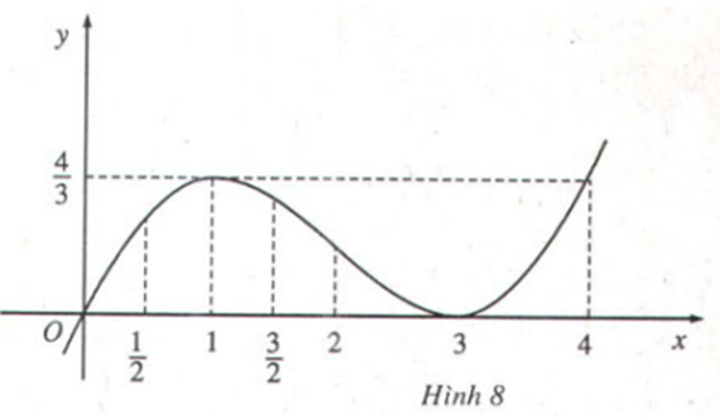
Dựa vào đồ thị (H.7, H.8 dưới đây, hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (hoặc nhỏ nhất):

a)

Phương pháp giải bài:

Quan sát đồ thị của hàm số trên và xét trong từng khoảng, tìm những điểm cao nhất (ứng với giá trị lớn nhất) và những điểm thấp nhất (ứng với giá trị nhỏ nhất).

Lời giải chi tiết:

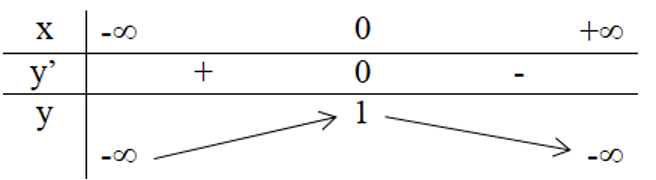
Từ đồ thị của hàm số ta thấy, tại điểm x=0  hàm số có giá trị lớn nhất bằng 1.

Xét dấu đạo hàm trên bảng biến thiên:

b)

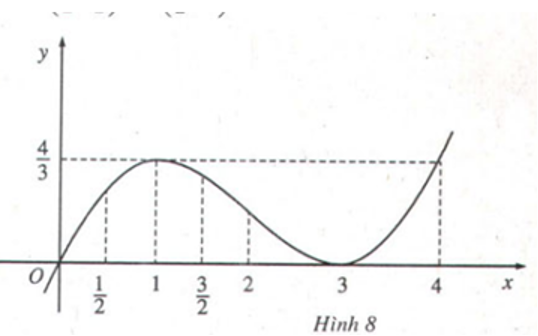
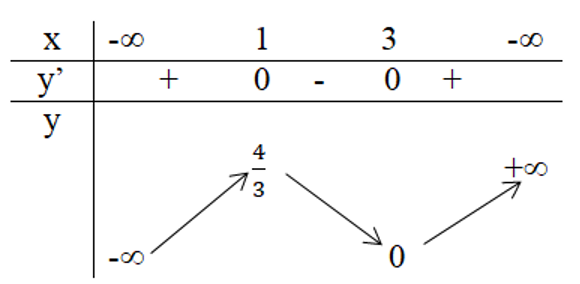
Lời giải chi tiết:

Từ đồ thị của hàm số ta thấy:

Tại điểm x=1 hàm số có giá trị lớn nhất bằng 43.

Tại điểm x=3 hàm số có giá trị nhỏ nhất bằng 0.

Xét dấu đạo hàm trên bảng biến thiên:

Trả lời câu hỏi 2 trang 14 SGK Giải tích 12 tập 1:

Đề bài:

Lời giải chi tiết:

Trả lời câu hỏi 3 trang 14 SGK Giải tích 12 tập 1:

a) Sử dụng đồ thị, hãy xét các hàm số sau đây có cực trị hay không 

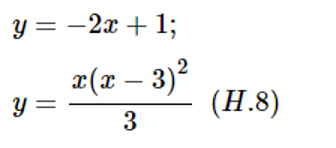
b) Nêu mối quan hệ giữa sự tồn tại của cực trị và dấu của đạo hàm.

Trả lời câu a:

Phương pháp giải:

Quan sát đồ thị, tìm các điểm cực trị ( cực đại:là điểm mà tại đó hàm số chuyển từ đồng biến sang nghịch biến, cực tiểu:là điểm mà tại đó hàm số chuyển từ nghịch biến sang đồng biến).

Lời giải chi tiết:

Trả lời câu b:

Lời giải chi tiết:

Nếu hàm số có các điểm cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.

Trả lời câu hỏi 4 trang 16 SGK Giải tích 12 tập 1

Đề bài

Hãy chứng minh hàm số y=|x| không có đạo hàm tại điểm x=0. Và hàm số có đạt cực trị tại điểm đó không ?

Phương pháp giải bài:

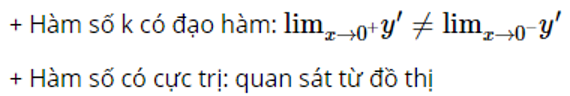
Lời giải chi tiết:

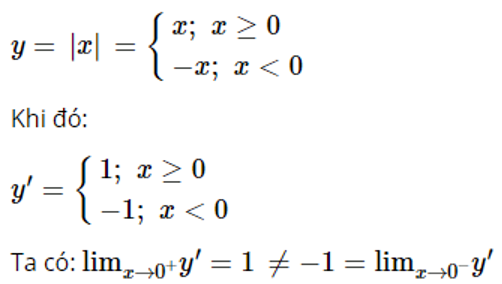
Vậy đạo hàm của hàm số không tồn tại tại điểm x=0.

Nhưng dựa vào đồ thị của hàm số y=|x|. Ta có hàm số đạt cực trị tại điểm x=0.

Trả lời câu hỏi 5 trang 16 SGK Giải tích 12 tập 1:

Đề bài:

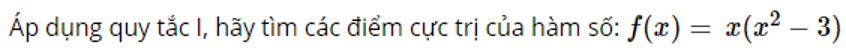
Lời giải chi tiết:

1. Tập xác định của hàm số: D=R.

3. Ta có bảng biến thiên như sau:

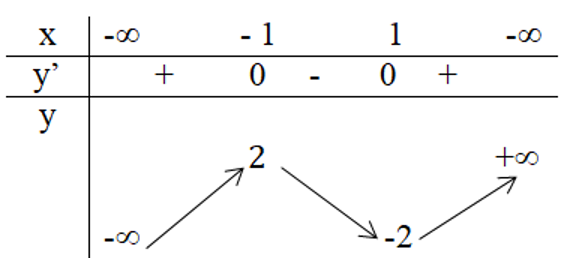
Hàm số đạt cực đại tại điểm x=−1 và giá trị cực đại là y=2

Hàm số đạt cực tiểu tại điểm x=1 và giá trị cực tiểu là y= −2.

Giải bài 1 trang 18 SGK Giải tích 12 tập 1:

a) Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau đây:

Phương pháp giải:

Quy tắc 1 tìm điểm cực trị của hàm số:

Bước 1: Tìm tập xác định (TXD) của hàm số.

Bước 2: Tính f′(x). Tìm các điểm mà tại đó f′(x) = 0 hoặc f′(x) không xác định.

Bước 3: Lập bảng biến thiên.

Bước 4: Từ bảng biến thiên sẽ suy ra các điểm cực trị.

Lời giải chi tiết:

Tập xác định của hàm số: D=R

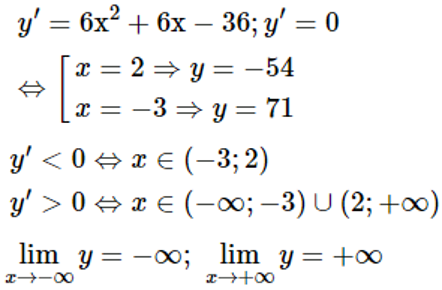
Lập bảng biến thiên:

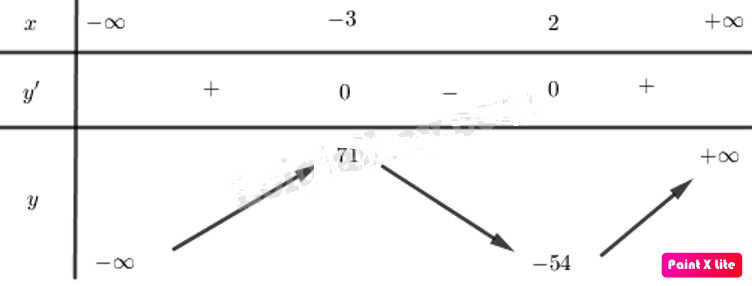
Hàm số đạt cực đại tại điểm x=−3 và  yCĐ =71

Hàm số đạt cực tiểu tại điểm x=2 và yCT =−54

b)

Lời giải chi tiết:

Tập xác định của hàm số: D=R

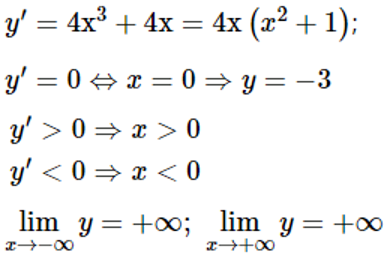
Lập bảng biến thiên:

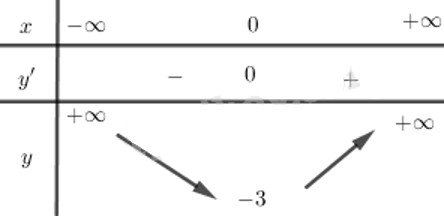
Hàm số đạt cực tiểu tại điểm x=0 và yCT =−3

c)

Lời giải chi tiết:

Tập xác định của hàm số: D=R\ { 0 }

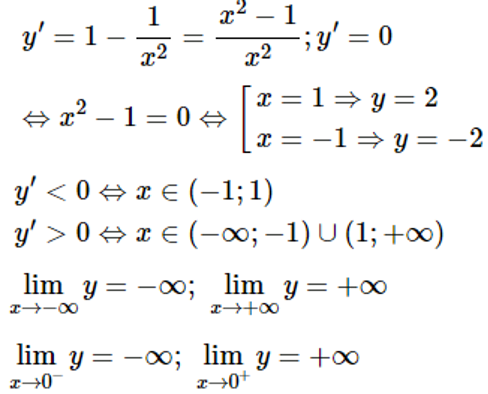
Lập bảng biến thiên:

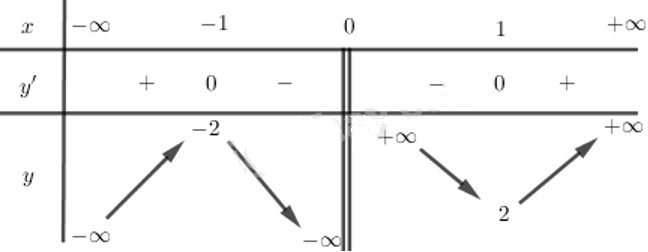
Hàm số đạt cực đại tại điểm x=−1 và yCĐ =−2

Hàm số đạt cực tiểu tại điểm x=1 và yCT  =2

d)

Lời giải chi tiết:

Tập xác định của hàm số :D=R

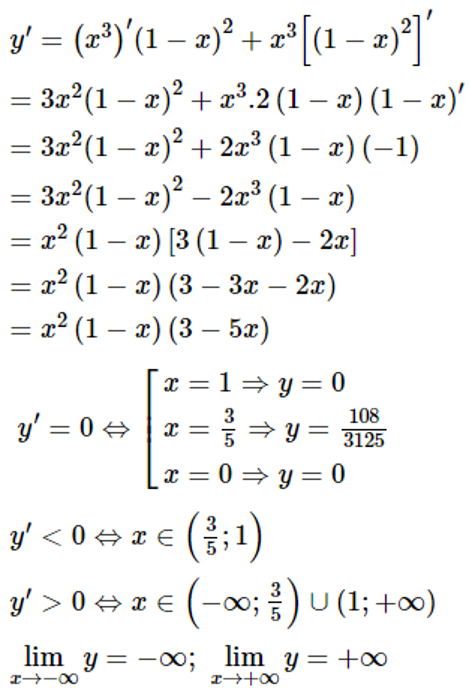
Lập bảng biến thiên:

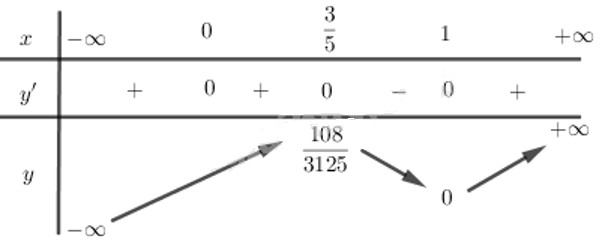
Hàm số đạt cực đại tại điểm x=35 và y=1083125

Hàm số đạt cực tiểu tại điểm x=1 và y =0

e)

Lời giải chi tiết:

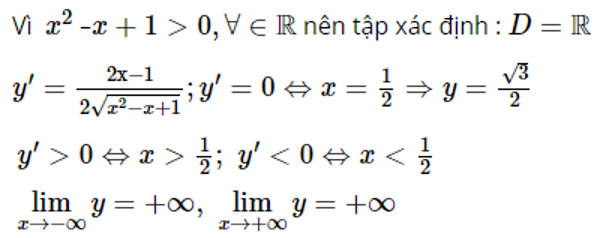
Lập bảng biến thiên:

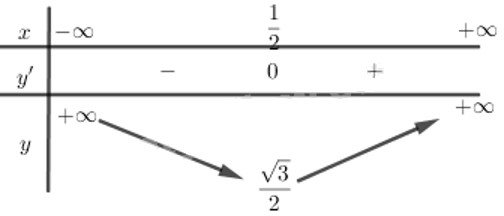
Giải bài 2 trang 18 SGK Giải tích 12 tập 1:

a)

Áp dụng quy tắc II, hãy tìm các điểm cực trị của hàm số sau đây:

Phương pháp giải:

Quy tắc II tìm các điểm cực trị của hàm số.

Bước 1: Tìm tập xác định (TXD)của hàm số đó.

Bước 2: Tính f′(x) và giải phương trình f′(x)=0 và kí hiệu xi(i=1,2,…,n) là các nghiệm của nó.

Bước 3: Tính f′′(x) và f′′(xi).

Bước 4: Dựa vào dấu của f′′(xi) sẽ suy ra tính chất cực trị của điểm xi.

Lời giải chi tiết:

Tập xác định của hàm số: D=R.

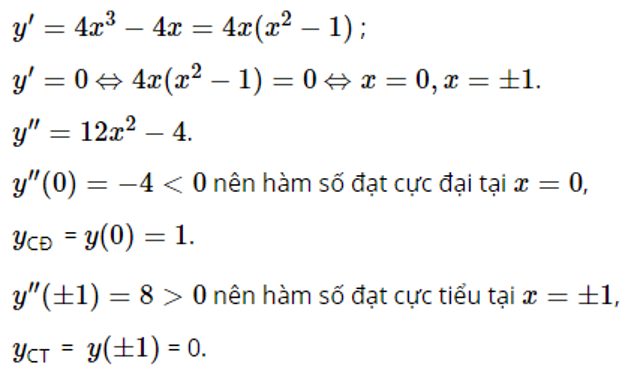
b)

y=sin2x–x

Phương pháp giải:

Quy tắc II tìm các điểm cực trị của hàm số.

Lời giải chi tiết:

Tập xác định của hàm số: D=R.

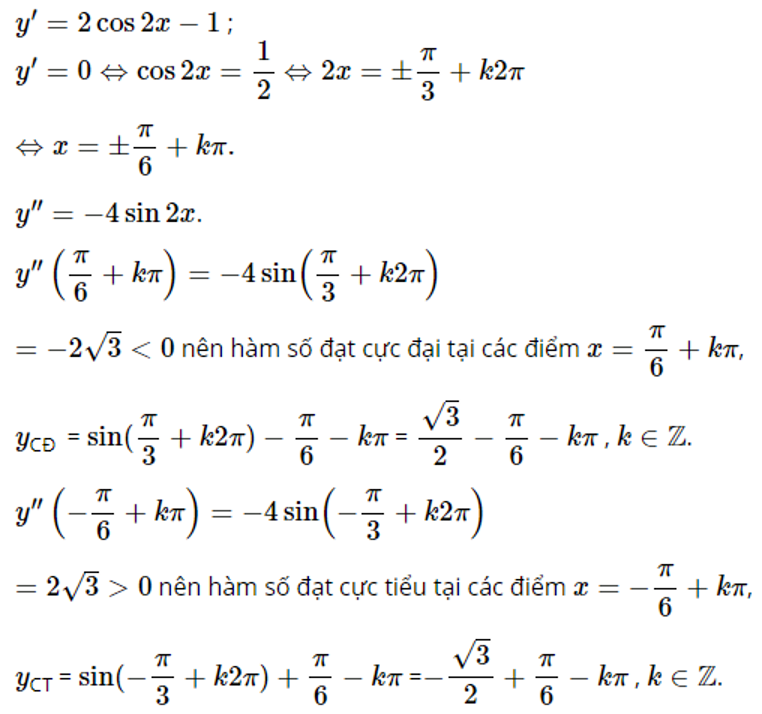
c)

y=sinx+cosx

Phương pháp giải:

Quy tắc II tìm các điểm cực trị của hàm số.

Lời giải chi tiết:

Tập xác định của hàm số: D=R

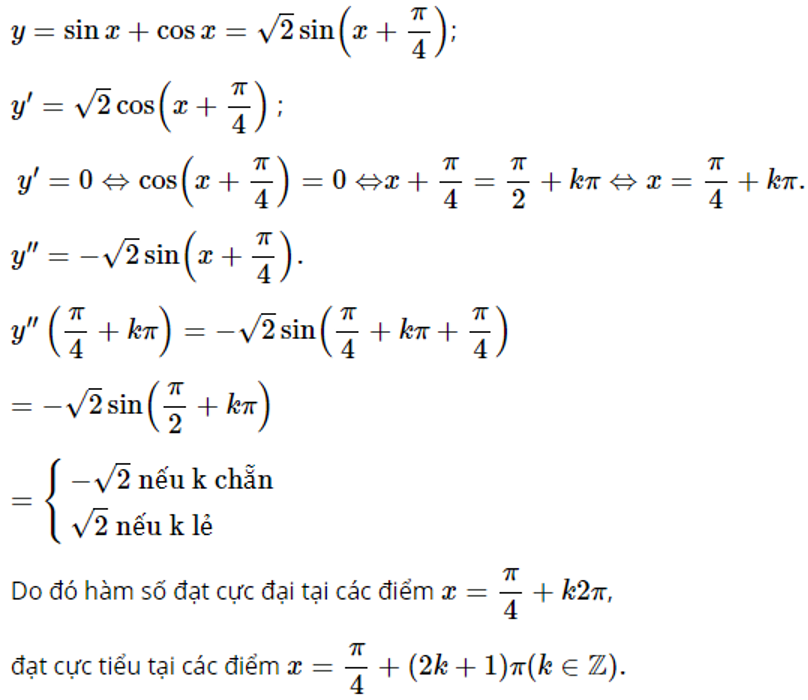
d)

Phương pháp giải:

Quy tắc II tìm các điểm cực trị của hàm số.

Lời giải chi tiết:

Tập xác định của hàm số: D=R.

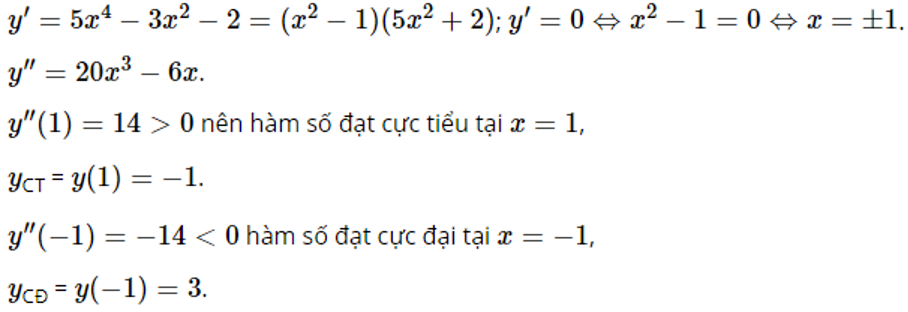
Giải bài 3 trang 18 SGK Giải tích 12 tập 1:

Đề bài:

Phương pháp giải bài:

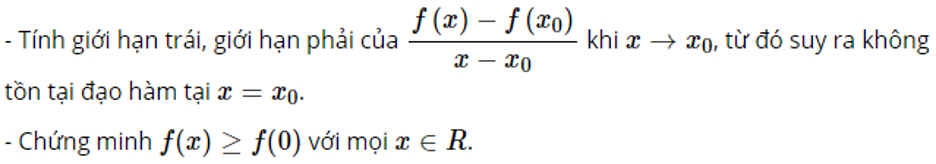
Lời giải chi tiết

Ta có:

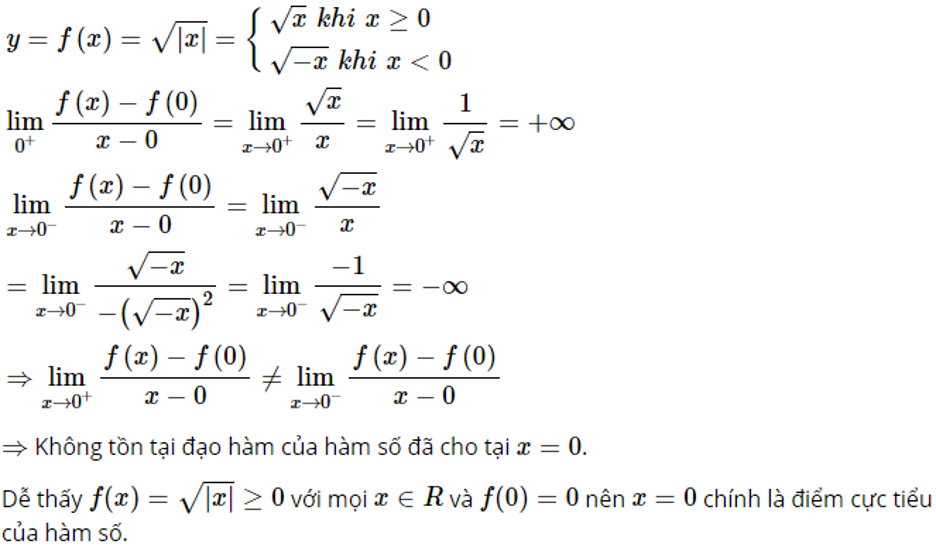
Giải bài 4 trang 18 SGK Giải tích 12 tập 1:

Đề bài:

Chứng minh rằng với tất cả giá trị của tham số m thì hàm số

luôn luôn sẽ có một điểm cực đại và một điểm cực tiểu.

Phương pháp giải bài:

B1: Tính y′

B2: Chứng tỏ rằng phương trình y′=0 luôn có 2 nghiệm phân biệt, với mọi m

Từ đó suy ra dấu của y′ và sự tồn tại của điểm cực đại cực tiểu.

Lời giải chi tiết

Tập xác định: D=R.

Từ bảng biến thiên ta thấy hàm số đạt cực đại tại x=x1 và đạt cực tiểu tại x=x2.

Vậy hàm số sẽ luôn có một cực đại và một cực tiểu.

Giải bài 5 trang 18 SGK Giải tích 12 tập 1:

Đề bài: Tìm a và b để các điểm cực trị của hàm số

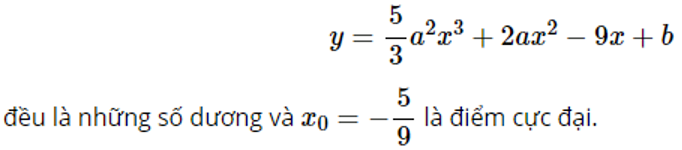
Phương pháp giải bài:

– Thay a vừa tìm được ở phía trên vào hàm số.

Tìm b dựa vào điều kiện: Hàm số đã cho có các cực trị đều dương ⇔yCT>0

Lời giải chi tiết:

 

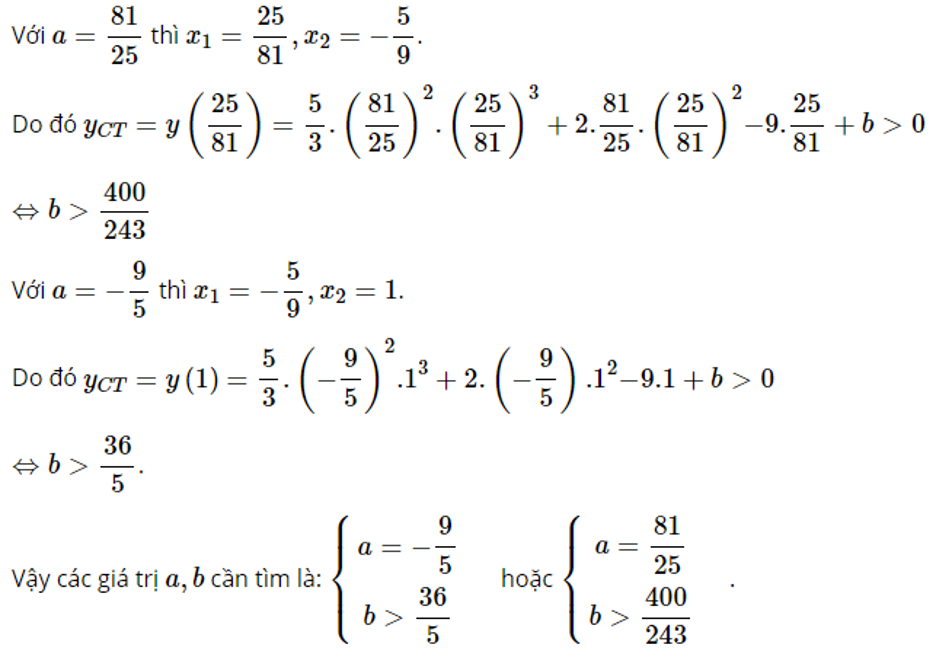
Giải bài 6 trang 18 SGK Giải tích 12 tập 1:

Đề bài:

Phương pháp giải bài:

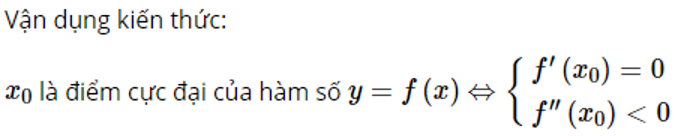
Lời giải chi tiết:

Tập xác định của hàm số là: D=R∖{−m};

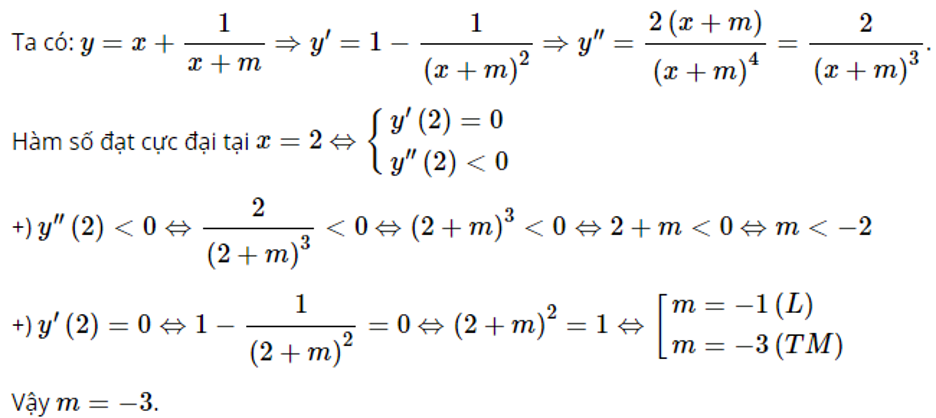
Tham khảo thêm:

• Tìm m để hàm số không có cực trị
• Tìm m để hàm số có 7 cực trị
• Tìm m để hàm số có 5 cực trị
• Tìm m để hàm số có 3 cực trị
• Tìm m để hàm số có 2 cực trị
• Tìm m để hàm số có đúng 1 cực trị
• Cực trị hàm trị tuyệt đối