Lý Thuyết Hình Học 10 Chương 1 Bài 3

Lý thuyết Hình học 10 chương 1 bài 3 Lý thuyết Tích của vectơ với một số Tải về Lớp: Lớp 10 Môn: Toán Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Lý thuyết hình học 10

VnDoc gửi đến quý thầy cô cùng các em học sinh tài liệu Lý thuyết Hình học 10 chương 1 bài 3, với nội dung được biên soạn kỹ lưỡng, bám sát kiến thức trọng tâm bài học, hỗ trợ quá trình dạy và học môn Toán lớp 10 đạt kết quả cao.

Lý thuyết Hình học 10 chương 1 bài 2

Lý thuyết Hình học 10 chương 1 bài 4

Hình học 10 - Lý thuyết Tích của vectơ với một số

1. Định nghĩa.

Tích của vectơ \(\underset{a}{\rightarrow}\) (khác \(\underset{0}{\rightarrow}\)) với số thực k (khác 0) là một vectơ, kí hiệu là k\(\underset{a}{\rightarrow}\), có độ dài bằng |k|\(\underset{a}{\rightarrow}\)| và:

- Cùng hướng với \(\underset{a}{\rightarrow}\) nếu k > 0 ;

- Ngược hướng với \(\underset{a}{\rightarrow}\) nếu k < 0.

Quy ước: k.\(\underset{0}{\rightarrow}\) = 0.\(\underset{a}{\rightarrow}\) = \(\underset{0}{\rightarrow}\), ∀k ∈ R, ∀ \(\underset{a}{\rightarrow}\)

Chú ý: 1. \(\underset{a}{\rightarrow}\) = \(\underset{a}{\rightarrow}\); (-1).\(\underset{a}{\rightarrow}\) = - \(\underset{a}{\rightarrow}\). Hiển nhiên vectơ \(\underset{a}{\rightarrow}\)/|\(\underset{a}{\rightarrow}\)| có độ dài bằng 1 (\(\underset{a}{\rightarrow}\) ≠0).

2. Các tính chất.

Với mọi vectơ \(\underset{a}{\rightarrow}\), \(\underset{b}{\rightarrow}\) và mọi số thực k, l ta có

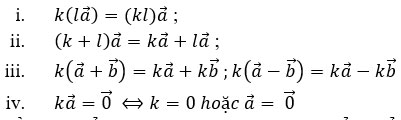
3. Điều kiện để hai vectơ cùng phương, ba điểm thẳng hàng.

Định lí 1: Cho \(\underset{a}{\rightarrow}\) ≠ \(\underset{0}{\rightarrow}\) và vectơ \(\underset{b}{\rightarrow}\). Khi đó \(\underset{b}{\rightarrow}\) và \(\underset{a}{\rightarrow}\) cùng phương <=> ∃k∈ R∶ \(\underset{b}{\rightarrow}\) = k\(\underset{a}{\rightarrow}\).

Hệ quả: Ba điểm A, B, C thẳng hàng khi và chỉ khi tồn tại k ∈ R để \(\underset{AB}{\rightarrow}\) = k\(\underset{AC}{\rightarrow}\)

4. Điều kiện để một điểm là trung điểm của một đoạn thẳng.

Cho đoạn thẳng AB. Điểm I là trung điểm của AB khi và chỉ khi \(\underset{IA}{\rightarrow}\) + \(\underset{IB}{\rightarrow}\) = \(\underset{0}{\rightarrow}\).

Hệ quả. Cho đoạn thẳng AB. Điểm I là trung điểm của AB khi và chỉ khi với điểm M bất kì ta có

\(\underset{MI}{\rightarrow}\) = (1/2).(\(\underset{MA}{\rightarrow}\) + \(\underset{MB}{\rightarrow}\)) (1)

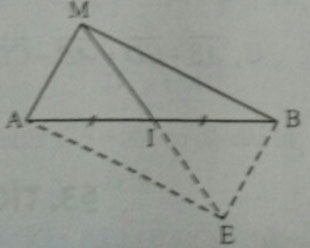
Nhận xét: Khi M không nằm trên đường thẳng AB, hệ thức (1) chính là hệ quả trực tiếp của quy tắc hình bình hành. Hệ thức này thường xuyên được sử dụng để giải các bài toán hình học, còn được gọi là “quy tắc trung điểm”.