Lý Thuyết Những Hằng đẳng Thức đáng Nhớ (năm 2022 + Bài Tập)

Trang chủ » Những Hdt đáng Nhớ » Lý Thuyết Những Hằng đẳng Thức đáng Nhớ (năm 2022 + Bài Tập)

Có thể bạn quan tâm

Lý thuyết Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ

Bài giảng Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ

A. Lý thuyết

1. Bình phương của một tổng

Bình phương của một tổng bằng bình phương số thứ nhất cộng hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A + B)2 = A2 + 2AB + B2.

Ví dụ 1:

(x + 3)2 = x2 + 2.x.3 + 32 = x2 + 6x + 9.

(2a + b)2 = (2a)2 + 2.2a.b + b2 = 4a2 + 4ab + b2.

2. Bình phương của một hiệu.

Bình phương của một hiệu bằng bình phương số thứ nhất trừ hai lần tích số thứ nhất và số thứ hai cộng bình phương số thứ hai.

Với A, B là các biểu thức tùy ý, ta có: (A – B)2 = A2 – 2AB + B2.

Ví dụ 2:

y−142=y2−2.y.14+142=y2-12y+116

(3x – y)2 = (3x)2 – 2.3x.y + y2 = 9x2 – 6xy + y2.

3. Hiệu hai bình phương

Hiệu hai bình phương bằng tích của hiệu với tổng của chúng.

Với A, B là các biểu thức tùy ý, ta có: A2 – B2 = (A – B)(A + B).

Ví dụ 3:

m2 – 4 = m2 – 22 = (m – 2)(m + 2)

(2a – b)(2a + b) = (2a)2 – b2 = 4a2 – b2

B. Bài tập tự luyện.

Bài 1: Khai triển các hằng đẳng thức sau:

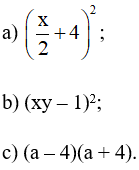
Lý thuyết Những hằng đẳng thức đáng nhớ chi tiết – Toán lớp 8 (ảnh 1)

Lời giải:

a)

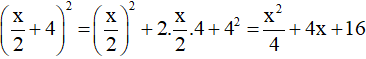
Lý thuyết Những hằng đẳng thức đáng nhớ chi tiết – Toán lớp 8 (ảnh 1)

b) (xy – 1)2 = (xy)2 – 2xy.1 + 12 = x2y2 – 2xy + 1.

c) (a – 4)(a + 4) = a2 – 42 = a2 – 16.

Bài 2: Viết lại các biểu thức sau dưới dạng bình phương của một tổng hoặc của một hiệu:

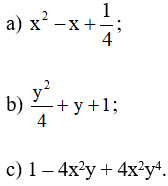
Lý thuyết Những hằng đẳng thức đáng nhớ chi tiết – Toán lớp 8 (ảnh 1)

Lời giải:

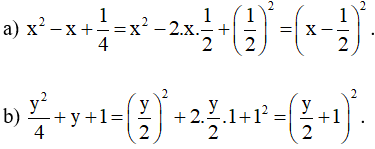
Lý thuyết Những hằng đẳng thức đáng nhớ chi tiết – Toán lớp 8 (ảnh 1)

c) 1 – 4xy2 + 4x2y4 = 1 – 2.1.2xy2 + (2xy2)2 = (1 – 2xy2)2.

Bài 3: Rút gọn các biểu thức sau:

a) A = (3x + y)2 – (y – 3x)2;

b) B = x4 + 2(y2 + 2xy)x2 + (y2 + 2xy)2.

Lời giải:

a) A = (3x + y)2 – (y – 3x)2

A = [(3x + y) – (y – 3x)][(3x + y) + (y – 3x)]

A = (3x + y – y + 3x)(3x + y + y – 3x)

A = 6x.2y

A= 12xy

b) B = x4 + 2(y2 + 2xy)x2 + (y2 + 2xy)2

B = (x2)2 + 2(y2 + 2xy)x2 + (y2 + 2xy)2

B = (x2 + y2 + 2xy)2

B = (x2 + 2xy + y2)2

B = ((x + y)2)2

B = (x + y)4

Bài 4: Viết các biểu thức sau thành đa thức:

a) (3x+4)^{2}

b) (5x-y)^{2}

c) (xy-\frac{1}{2}y)^{2}

Lời giải:

a) (3x+4)^{2}=9x^{2}+24x+16

b) (5x-y)^{2}=25x^{2}-10xy+y^{2}

c) (xy-\frac{1}{2}y)^{2}=x^{2}y^{2}-xy^{2}+\frac{1}{4}y^{2}

Bài 5: Tính nhanh

a) 38 \times 42

b) 102^{2}

c) 198^{2}

d) 75^{2}-25^{2}

Lời giải:

a) 38 \times 42 = (40-2)(40+2)

=40^{2}-2^{2}=1600-4=1598

b) 102^{2}=(100+2)^{2}=100^{2}+2\times 100 \times 2 +2^{2}

=10000+400+4=10404

c) 198^{2}=(200-2)^{2}=200^{2}- 2 \times 200 \times 2+2^{2}

=40000-800+4=39204

d) 75^{2}-25^{2}=(75-25)(75+25)=50\times 100=5000

Bài 6: Tìm giá trị nhỏ nhất của biểu thức sau:

A = 2x2 – 4x + 4xy + 4y2 – 1.

Lời giải:

Ta có:

A = 2x2 – 4x + 4xy + 4y2 – 1

A = x2 – 4x + 4 + x2 + 4xy + 4y2 – 5

A = (x – 2)2 + (x + 2y)2 – 5

Vì (x – 2)2 ≥ 0 với mọi x; (x + 2y)2 ≥ 0 với mọi x; y.

Do đó A ≥ – 5 với mọi x; y.

Dấu “=” xảy ra khi và chỉ khi x−2=0x+2y=0⇒x=2y=−1.

Vậy giá trị nhỏ nhất của A bằng –5 đạt được khi x = 2 và y = –1.

Bài 7: Tìm giá trị lớn nhất của các biểu thức dưới đây:

a, A = 5x - {x^2}

b, B = - {x^2} + 2x + 9

Gợi ý đáp án

a, A = 5x - {x^2} = - \left( {{x^2} - 2.\frac{5}{2}x + \frac{{25}}{4}} \right) + \frac{{25}}{4} = - {\left( {x - \frac{5}{2}} \right)^2} + \frac{{25}}{4}

Có - {\left( {x - \frac{5}{2}} \right)^2} \le 0\forall x \Rightarrow - {\left( {x - \frac{5}{2}} \right)^2} + \frac{{25}}{4} \le \frac{{25}}{4}

Dấu “=” xảy ra \Leftrightarrow x = \frac{5}{2}

Vậy \max A = \frac{{25}}{4} \Leftrightarrow x = \frac{5}{2}

b, B = - {x^2} + 2x + 9 = - \left( {{x^2} - 2x + 1} \right) + 10 = - {\left( {x - 1} \right)^2} + 10

Có - {\left( {x - 1} \right)^2} \le 0\forall x \Rightarrow - {\left( {x - 1} \right)^2} + 10 \le 10

Dấu “=” xảy ra \Leftrightarrow x = 1

Vậy max B = 10 khi và chỉ khi x = 1

Trắc nghiệm Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ

Bài 1: Chọn câu đúng

A. 4 – (a + b)2 = (2 + a + b)(2 – a + b)

B. 4 – (a + b)2 = (4 + a + b)(4 – a – b)

C. 4 – (a + b)2 = (2 + a – b)(2 – a + b)

D. 4 – (a + b)2 = (2 + a + b)(2 – a – b)

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có 4 – (a + b)2 = 22 – (a + b)2

= (2 + a + b)[2 – (a + b)]

= (2 + a + b)(2 – a – b)

Bài 2: Biểu thức (a – b – c)2 bằng

A. a2 + b2 + c2 – 2(bc + ac + ab)

B. a2 + b2 + c2 + bc – ac – 2ab

C. a2 + b2 + c2 + 2(bc – ac – ab)

D. a2 + b2 + c2 + 2(bc – ac – ab)

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có (a - b - c)2 = [(a - b) - c]2

= (a - b)2 - 2(a - b).c + c2

= a2 - 2ab + b2 - 2ac + 2bc + c2

= a2 + b2 + c2 + 2(bc – ac – ab)

Bài 3: Chọn câu đúng.

A. (A + B)2 = A2 + 2AB + B2

B. (A + B)2 = A2 + AB + B2

C. (A + B)2 = A2 + B2

D. (A + B)2 = A2 – 2AB + B2

Hiển thị đáp án

Đáp án: A

Giải thích: Ta có (A + B)2 = A2 + 2AB + B2

Bài 4: Chọn câu sai.

A. (x + y)2 = (x + y)(x + y)

B. x2 – y2 = (x + y)(x – y)

C. (-x – y)2 = (-x)2 – 2(-x)y + y2

D. (x + y)(x + y) = y2 – x2

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có (x + y)(x + y) = (x + y)2

= x2 + 2xy + y2 ≠ y2 – x2

nên câu D sai.

Bài 5: Chọn câu sai.

A. (x + 2y)2 = x2 + 4xy + 4y2

B. (x – 2y)2 = x2 – 4xy + 4y2

C. (x – 2y)2 = x2 – 4y2

D. (x – 2y)(x + 2y) = x2 – 4y2

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

(x + 2y)2 = x2 + 2x.2y + (2y)2

= x2 + 4xy + 4y2 nên A đúng

(x – 2y)2 = x2 – 2x.2y + (2y)2

= x2 – 4xy + 4y2 nên B đúng, C sai.

(x – 2y)(x + 2y) = x2 – (2y)2

= x2 – 4y2 nên D đúng

Bài 6: Chọn câu đúng.

A. (A – B)(A + B) = A2 + 2AB + B2

B. (A + B)(A – B) = A2 – B2

C. (A + B)(A – B) = A2 – 2AB + B2

D. (A + B)(A – B) = A2 + B2

Hiển thị đáp án

Đáp án: B

Giải thích: Ta có A2 – B2 = (A – B)(A + B)

Bài 7: Khai triển 4x2 – 25y2

theo hằng đẳng thức ta được

A. (4x – 5y)(4x + 5y)

B. (4x – 25y)(4x + 25y)

C. (2x – 5y)(2x + 5y)

D. (2x – 5y)2

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

x2 – 25y2 = (x)2 – (5y)2

= (x – 5y)(x + 5y)

Bài 8: Khai triển 19x2−164y2 theo hằng đẳng thức ta được

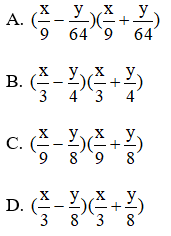
Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án - Toán lớp 8 (ảnh 1)

Hiển thị đáp án

Đáp án: D

Giải thích:

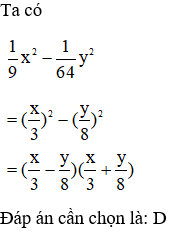
Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án - Toán lớp 8 (ảnh 1)

Bài 9: Khai triển (3x – 4y)2 ta được

A. 9x2 – 24xy + 16y2

B. 9x2 – 12xy + 16y2

C. 9x2 – 24xy + 4y2

D. 9x2 – 6xy + 16y2

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có (3x – 4y)2

= (3x)2 – 2.3x.4y + (4y)2

= 9x2 – 24xy + 16y2

Bài 10: Khai triển (x2−2y)2 ta được

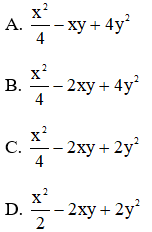
Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án - Toán lớp 8 (ảnh 1)

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có (x2−2y)2

= (x2)2−2.x2.2y+(2y)2

=x24−2xy+4y2

Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo)

Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo)

Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử

Từ khóa » Những Hdt đáng Nhớ