Lý Thuyết Toán 10 Phương Trình Đường Thẳng - Marathon Education

Warning: mysqli_query(): (HY000/1): Can't create/write to file '/tmp/#sql-temptable-b851-3067db-30cca.MAI' (Errcode: 28 "No space left on device") in /opt/bitnami/wordpress/wp-includes/wp-db.php on line 2162

Ở chương trình Toán lớp 10 các em sẽ được tiếp xúc với các lý thuyết và dạng toán về phương trình đường thẳng. Đây là nền tảng kiến thức liên quan mật thiết đến hình học không gian ở các lớp sau, do đó các em cần nắm thật vững những kiến thức này. Trong bài viết này, Marathon Education sẽ tổng hợp các lý thuyết Toán 10 phương trình đường thẳng nhằm giúp các em hệ thống hóa được kiến thức và nhớ bài dễ dàng hơn.

>>> Xem thêm: Lý Thuyết Toán 10 Phương Trình Đường Tròn

>>> Xem thêm: Học Toán lớp 10 Online Hiệu Quả Cùng Marathon Education

Vectơ của đường thẳng

Vectơ chỉ phương

\begin{aligned} &\footnotesize\text{Vectơ } \vec{u}\text{ được gọi là vectơ chỉ phương (VTCP) của đường thẳng ∆ nếu:}\\ &\footnotesize \ \ \bull \vec{u} \not= \vec{0}\\ &\footnotesize \ \ \bull \text{Giá của } \vec{u} \text{ song song hoặc trùng với ∆} \end{aligned}

Chú ý: Một đường thẳng sẽ có vô số vectơ chỉ phương.

Vectơ pháp tuyến

\begin{aligned} &\footnotesize\text{Vectơ } \vec{n}\text{ được gọi là vectơ pháp tuyến (VTPT) của đường thẳng ∆ nếu:}\\ &\footnotesize \ \ \bull \vec{n} \not= \vec{0}\\ &\footnotesize \ \ \bull \vec{n} \text{ vuông góc với VTCP của ∆} \end{aligned}

Chú ý:

\begin{aligned} &\footnotesize \bull \text{Một đường thẳng sẽ có vô số vectơ pháp tuyến.}\\ &\footnotesize \bull \text{Nếu }\vec{n} \text{ là một VTPT của đường thẳng ∆ thì } k\vec{n} \text{ cũng là một vectơ pháp tuyến của ∆.}\\ &\footnotesize\bull \text{Một đường thẳng được hoàn toàn xác định nếu biết một vectơ pháp tuyến của nó và}\\ &\footnotesize \text{một điểm mà đường thẳng đó đi qua.} \end{aligned}

>>> Xem thêm: Cách Giải Các Dạng Toán Phương Trình Đường Thẳng Trong Không Gian

Hàm Số Lượng Giác 11 - Lý Thuyết Và Các Công Thức Cơ Bản Cần Nhớ

Các dạng phương trình đường thẳng

Dưới đây là tổng hợp các dạng phương trình đường thẳng Toán 10.

Phương trình tham số của đường thẳng

Xét đường thẳng ∆ đi qua điểm xác định M0(x0; y0) với VTCP:

\vec{u}=(u_1;u_2)

Phương trình tham số của đường thẳng ∆ là:

\begin{cases} x=x_0+tu_1\\ y=y_0+tu_2 \end{cases}

Với một tham số t cụ thể, ta xác định được một điểm trên đường thẳng ∆.

ĐĂNG KÝ NGAY

Mối liên hệ giữa VTPT và hệ số góc:

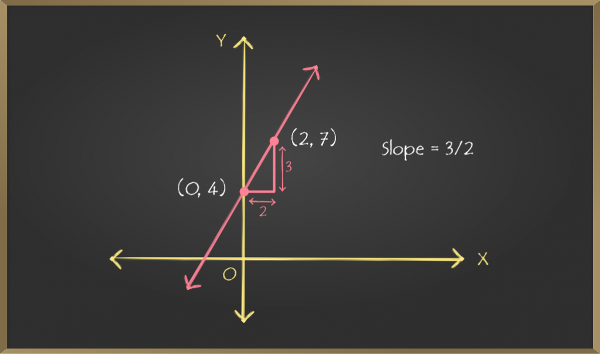
\begin{aligned} &\footnotesize\text{Tỉ số }k=\frac{u_2}{u_1} \text{ được gọi là hệ số góc của đường thẳng ∆ }(u_1\not= 0), \text{k = tanα, với α là góc hợp bởi đường thẳng ∆ }\\ &\footnotesize\text{và chiều dương của trục Ox.} \end{aligned}

Phương trình đường thẳng đi qua Mo(xo; yo), có hệ số góc là k:

y – y0 = k(x – x0)

Phương trình tổng quát của đường thẳng

Phương trình tổng quát của đường thẳng có dạng:

ax + by + c = 0 (a≠0 hoặc b≠0)

Nhận xét:

\begin{aligned} &\footnotesize\bull \text{Nếu }a=0\Rightarrow y=-\frac{c}{b}\ ; \Delta//Ox \text{ hoặc trùng Ox (khi c = 0)}\\ &\footnotesize\bull \text{Nếu }b=0\Rightarrow x=-\frac{c}{a}\ ; \Delta//Oy \text{ hoặc trùng Oy (khi c = 0)}\\ &\footnotesize\bull \text{Nếu }c=0\Rightarrow ax+by=0 \Rightarrow\Delta \text{ đi qua gốc tọa độ} \end{aligned}

Phương trình đoạn chắn của đường thẳng

Một đường thẳng cắt trục Ox và Oy tại 2 điểm lần lượt là A(a;0), B(0;b) có phương trình đoạn chắn như sau:

\frac{x}{a}+\frac{y}{b}=1\ (a,b\not=0)

Phương trình chính tắc của đường thẳng

\footnotesize \text{Đường thẳng ∆ có VTCP }\vec{u}=(u_1;u_2), \text{ đi qua điểm }M_0(x_0;y_0) \text{ có phương trình chính tắc là:}\\ \normalsize \frac{x-x_0}{u_1}=\frac{y-y_0}{u_2} \text{ với }u_1,u_2\not=0

Vị trí tương đối của hai đường thẳng

Xét 2 đường thẳng:

Công Thức Tính Đạo Hàm Căn Bậc 3 Và Một Số Ví Dụ Minh Họa

∆1: a1x + b1y + c1 = 0

∆2: a2x + b2y + c2 = 0

M0(x0;y0) là điểm chung của ∆1 và ∆2 khi và chỉ khi (x0;y0) là nghiệm của hệ phương trình sau:

(1)\begin{cases}a_1x+b_1y+c=0\\a_2x+b_2y+c=0 \end{cases}

Khi đó, sẽ có 3 trường hợp xảy ra:

• Hệ (1) có một nghiệm: ∆1 cắt ∆2
• Hệ (1) vô nghiệm: ∆1 // ∆2
• Hệ (1) có vô số nghiệm: ∆1 ≡ ∆2

Góc giữa hai đường thẳng

Đây là một trong những kiến thức quan trọng trong Toán 10 phương trình đường thẳng mà các em cần lưu tâm.

Xét 2 đường thẳng ∆1 và ∆2:

• 2 đường thẳng cắt nhau sẽ tạo thành 4 góc, khi đó:
  • Nếu ∆1 vuông góc với ∆2 → góc giữa 2 đường thẳng = 900.
  • Nếu ∆1 và ∆2 không vuông góc với nhau → góc giữa 2 đường thẳng là góc nhọn trong số 4 góc được tạo thành.
• Nếu ∆1 và ∆ 2 song song hoặc trùng nhau → góc giữa 2 đường thẳng này = 00.

\begin{aligned} &\text{Góc giữa 2 đường thẳng ∆1 và ∆2 kí hiệu là }(\widehat{\Delta_1,\Delta_2}) \text{ và được xác định theo công thức:}\\ &∆_1: a_1x+b_1y+c_1=0\\ &∆_2: a_2x+b_2y+c_2=0\\ &\text{Đặt }\varphi=(\widehat{\Delta_1,\Delta_2})\\ &cos\varphi=\frac{|a_1.a_2+b_1.b_2|}{\sqrt{a_1^2+b_1^2}\sqrt{a_2^2+b_2^2}} \end{aligned}

Chú ý:

• ∆1 ⊥ ∆2 ⇔ n1 ⊥ n2 ⇔ a1.a2 + b1.b2 = 0
• Nếu ∆1 và ∆2 có phương trình y = k1x + m1 và y = k2x + m2 thì ∆1 ⊥ ∆2 ⇔ k1.k2 = -1

Khoảng cách từ 1 điểm đến đường thẳng

Cho một điểm M0(x0;y0) và đường thẳng ∆ bất kỳ có phương trình tổng quát là ax + by + c = 0. Khoảng cách từ điểm M đến ∆ được xác định theo công thức sau:

d(M_0,\Delta)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}

Tham khảo ngay các khoá học online của Marathon Education

Gia sư Online Bí Quyết Học Tốt Toán 12 Và Đạt Điểm Cao Trong Kỳ Thi Đại Học Học Online Toán 12 Học Online Hóa 10 Học Online Toán 11 Học Online Toán 6 Học Online Toán 10 Học Online Toán 7 Học Online Lý 10 Học Online Lý 9 Học Online Toán 8 Học Online Toán 9 Học Tiếng Anh 6 Học Tiếng Anh 7

Trên đây là những lý thuyết Toán 10 phương trình đường thẳng các em nên ghi nhớ và luyện tập thường xuyên. Các em đừng quên đăng ký lớp học online livestream Toán – Lý – Hóa tại Marathon Education để cùng học tập hiệu quả hơn. Chúc các em luôn học tốt và luôn đạt 8+ trong các bài kiểm tra!