LÝ THUYẾT VÀ BÀI TẬP CHIA ĐA THỨC MỘT BIẾN ĐÃ SẮP XẾP
Có thể bạn quan tâm
LÝ THUYẾT VÀ BÀI TẬP
CHIA ĐA THỨC MỘT BIẾN ĐÃ SẮP XẾP
A. Tóm tắt kiến thức
1. Phương pháp:
Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B ≠0 tồn tại duy nhất hai đa thức Q và R sao cho:
A = B . Q + R, với R = 0 hoặc bậc bé hơn bậc của 1
Nếu R = 0, ta được phép chia hết.
Nếu R ≠0, ta được phép chia có dư.
B. Bài tập:
Bài 1
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:
a) (x3 – 7x + 3 – x2) : (x – 3);
b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2).
Đáp án và hướng dẫn giải bài:
a) (x3 – 7x + 3 – x2) : (x – 3)
Sắp xếp lại: (x3 – x2 – 7x + 3 ) : (x – 3)

b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2)
Sắp xếp lại: (2x4 – 3x2 – 3x2 + 6x – 2) : (x2 – 2)

Bài 2
Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:
a) (x2 + 2xy + y2) : (x + y);
b) (125x3 + 1) : (5x + 1);
c) (x2 – 2xy + y2) : (y – x).
Đáp án và hướng dẫn giải bài:
a) (x2 + 2xy + y2) : (x + y) = (x + y)2 : (x + y) = x + y.
b) (125x3 + 1) : (5x + 1) = [(5x)3 + 1] : (5x + 1)
= (5x)2 – 5x + 1 = 25x2 – 5x + 1.
c) (x2 – 2xy + y2) : (y – x) = (x – y)2 : [-(x – y)] = – (x – y) = y – x
Hoặc (x2 – 2xy + y2) : (y – x) = (y2 – 2xy + x2) : (y – x)
= (y – x)2 : (y – x) = y – x.
Bài 3
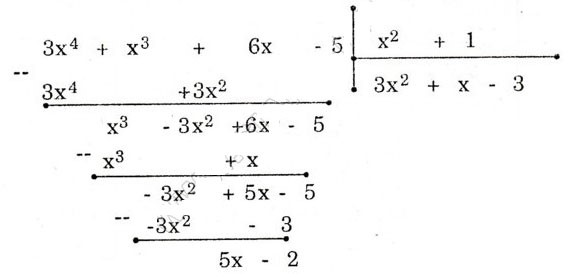
Cho hai đa thức A = 3x4 + x3 + 6x – 5 và B = x2+ 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R.
Đáp án và hướng dẫn giải bài:
Vậy 3x4 + x3 + 6x – 5 = (x2+ 1)(3x2 + x – 3) + 5x – 2
Bài 4
Làm tính chia:
a) (25x5 – 5x4 + 10x2) : 5x2;
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y.
Đáp án và hướng dẫn giải bài:
a) (25x5 – 5x4 + 10x2) : 5x2 = (25x5 : 5x2 ) – (5x4 : 5x2 ) + (10x2 : 5x2) = 5x3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y
= (15x3y2 : 6x2y) + (– 6x2y : 6x2y) + (– 3x2y2 : 6x2y)
= 15/6xy – 1 – 3/6y = 5/2xy – 1/2y – 1.
Bài 5
Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không.
a) A = 15x4 – 8x3 + x2
B = 1/2x2
b) A = x2 – 2x + 1
B = 1 – x
Đáp án và hướng dẫn giải bài:
a) Ta có 15x4 ; 8x3 ; x2 chia hết cho 1/2x2 nên đa thức A chia hết cho B.
b) A chia hết cho B, vì x2 – 2x + 1 = (1 – x)2, chia hết cho 1 – x
Bài 6
Làm tính chia:
(2x4 + x3 – 3x2 + 5x – 2) : (x2 – x + 1).
Đáp án và hướng dẫn giải bài
Khi đó :(2x4 + x3 – 3x2 + 5x – 2) = (x2 – x + 1)(2x3 + 3x – 2).

Bài 7
Tính nhanh:
a) (4x2 – 9y2) : (2x – 3y); b) (27x3 – 1) : (3x – 1);
c) (8x3 + 1) : (4x2 – 2x + 1); d) (x2 – 3x + xy -3y) : (x + y)
Đáp án và hướng dẫn giải bài:
a) (4x2 – 9y2) : (2x – 3y) = [(2x)2 – (3y)2] : (2x – 3y) = (2x –3y)(2x +3y) : (2x –3y) = 2x + 3y;
b) (27x3 – 1) : (3x – 1) = [(3x)3 – 1] : (3x – 1) = (3x – 1) [(3x)2 + 3x + 1] : (3x – 1) = 9x2+ 3x + 1
c) (8x3 + 1) : (4x2 – 2x + 1) = [(2x)3 + 1] : (4x2 – 2x + 1)
= (2x + 1)[(2x)2 – 2x + 1] : (4x2 – 2x + 1)
= (2x + 1)(4x2 – 2x + 1) : (4x2 – 2x + 1) = 2x + 1
d) (x2 – 3x + xy -3y) : (x + y)
= [(x2 + xy) – (3x + 3y)] : (x + y)
= [x(x + y) – 3(x + y)] : (x + y)
= (x + y)(x – 3) : (x + y)
= x – 3.
Bài 8
Tìm số a để đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2
Đáp án và hướng dẫn giải bài:
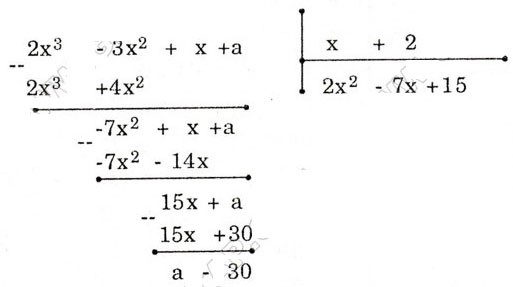
Khi đó 2x3 – 3x2 + x + a = (x + 2) (2x2 – 7x + 15) + a – 30 để đa thức 2x3 – 3x2 + x + a chia hết cho đa thức (x + 2) thì phần dư a – 30 = 0 hay a = 30.
Từ khóa » Cách Chia đa Thức Cho đa Thức Lớp 8
-
Chia đa Thức Cho đa Thức: Lý Thuyết, Ví Dụ Và Bài Tập - DINHNGHIA.VN
-
Chia đa Thức Cho đa Thức Toán Lớp 8 | Lý Thuyết Và Bài Tập Cơ Bản ...
-
Chia đa Thức Cho đa Thức: Lý Thuyết & Bài Tập
-
Cách Chia đa Thức Cho đa Thức [Lớp 8]: Lý Thuyết & Bài Tập Vận Dụng
-
Cách Chia đơn Thức Cho đơn Thức, đa Thức Cho đơn Thức Và đa ...
-
Chuyên đề: Chia đa Thức - Toán Lớp 8 - Trường Quốc Học
-
2 CÁCH CHIA ĐA THỨC CHO ĐA THỨC MỘT BIẾN VÀ HAI BIẾN
-
Cách Giải Bài Toán Dạng: Chia đa Thức Toán Lớp 8 | Chuyên đề Toán 8
-
Chia đa Thức Cho đa Thức - Toán Lớp 8
-
Lý Thuyết Chia đa Thức Cho đơn Thức | SGK Toán Lớp 8
-
Chương I. PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Giải Bài Tập Toán Lớp 8: Bài 12. Chia đa Thức Một Biến đã Sắp Xếp
-
SGK Toán 8 - Bài 11. Chia đa Thức Cho đơn Thức - Giải Bài Tập
-
Chia đa Thức Cho đơn Thức - Chuyên đề Toán Học Lớp 8