Nguyên Hàm | Đỗ Cao Long's Blog.

Có thể bạn quan tâm

Bỏ qua điều hướng
Chuyển đến nội dung chính
Skip to primary sidebar
Skip to secondary sidebar
Skip to footer

Đỗ Cao Long's Blog.

Dạy Toán cơ bản cho học sinh yếu môn Toán!

Trang chủ
About me
- Thi giải Toán trên Internet
- Lời tâm sự
BDHSG
- Chuyên đề phương trình – hệ phương trình
Geogebra
Giải đáp
Học Toán
- Toán 10
  - Đề thi thử hk2, Toán 10
  - BĐT Côsi (Cơ bản)
  - Tam thức bậc hai
  - Các bài của học sinh
- Đánh công thức Toán trên Blog wordpress
- Toán 11
  - Ôn tập chương II (Đại số 11)
  - Ôn tập học kỳ I (Toán 11)
  - Giới hạn hàm số
- Toán 12
  - Bài của học sinh
  - Chuyên đề PT Mũ-Lôgarit
  - Nguyên hàm
  - Phương trình đường thẳng
  - Đề cương ôn tập học kỳ 1-Toán 12
    - Hướng dẫn giải- Đáp số (Ôn tập Toán 12, học kỳ 1)
  - Tọa độ vectơ
  - Đề cương ôn thi Tốt ghiệp
- OTDH-P.H.E
  - Cực trị hình học giải tích
  - Giải đề thi thử đại học môn Toán 2010
  - Nguyên hàm-PP tính
  - Khảo sát hàm số
  - Đề thi thử Đại học 2009
    - Giải đề số 10
    - Giải đề số 11
    - Giải đề só 12
    - Giải đề số 13
    - Giải đề số 16
    - Giải đề số 08
    - Giải đề số 09
    - Giải đề số 14
    - Lời giải đề 06
    - Lời giải đề số 07
  - Tích phân-Ứng dụng
  - Đề thi lần 1. Lớp PHE
  - Đường thẳng trong không gian
Soft
Tài nguyên
Toán Blog

Nguyên hàm

Một số bài toán tìm nguyên hàm.

Ghi nhớ một số nguyên hàm cơ bản:

1. $\int \dfrac{dx}{x} = \ln |x| +C$

2. $\int \dfrac{dx}{x+a}=\ln|x+a|+C$

3. $\int\dfrac{dx}{ax+b}=\dfrac{1}{a}\int\dfrac{d(ax+b)}{ax+b}$ $= \dfrac{1}{a} \ln|ax+b|+C$

——————————————-

Bài 1: Tìm nguyên hàm $\int \dfrac{dx}{\sin x}$ .

Cách 1: Ta phân tích biểu thức dưới dấu nguyên hàm như sau:

$\dfrac{dx}{\sin x}=\dfrac{\sin x.dx}{\sin^2 x}$ $=\dfrac{-d(\cos x)}{1-\cos^2 x}$

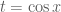Đặt $t=\cos x$ , khi đó nguyên hàm cần tìm được viết lại theo 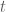$t$ như sau:

$\int \dfrac{-dt}{1-t^2}=\int \dfrac{dt}{t^2-1}=\dfrac{1}{2} \int (\dfrac{1}{t-1} -\dfrac{1}{t+1})dt$

$= \dfrac{1}{2} ( \int \dfrac{dt}{t-1} - \int \dfrac{dt}{t+1} )$ $= \dfrac{1}{2} ( \int \dfrac{d(t-1)}{t-1} - \int \dfrac{d(t+1)}{t+1} )$

$=\dfrac{1}{2} (\ln |t-1| - \ln |t+1|)+C =\dfrac{1}{2} \ln|\dfrac{t-1}{t+1}|+C$

Cuối cùng thay 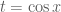$t=\cos x$ ta được:

$\int \dfrac{dx}{\sin x}= \dfrac{1}{2} \ln|\dfrac{\cos x -1}{\cos x+1}|+C$

———————————————

Cách 2: Dùng công thức góc nhân đôi ta có 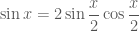$\sin x = 2\sin\dfrac{x}{2} \cos \dfrac{x}{2}$

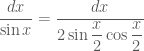
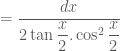Khi đó $\dfrac{dx}{\sin x} = \dfrac{dx}{2\sin\dfrac{x}{2} \cos \dfrac{x}{2}}$ $=\dfrac{dx}{2\tan\dfrac{x}{2} . \cos^2 \dfrac{x}{2}}$ .

Ta biết $\dfrac{dx}{2\cos^2 \dfrac{x}{2}} = d(\tan \dfrac{x}{2})$

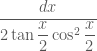
Suy ra $\dfrac{dx}{2\tan\dfrac{x}{2} \cos^2 \dfrac{x}{2}}$ $=\dfrac{1}{\tan \dfrac{x}{2}} .d(\tan \dfrac{x}{2})$

Vậy nguyên hàm đã cho được tính như sau:

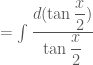
$\int \dfrac{dx}{\sin x}$ $= \int \dfrac{d(\tan \dfrac{x}{2})}{\tan \dfrac{x}{2}}$ $=\ln|\tan \dfrac{x}{2}|+C$ .

Chia sẻ:

Reddit
Thêm

Facebook

Thích Đang tải...

Bình luận về bài viết này
Comments 36

nguyễn thị phước | 19/02/2009 lúc 05:08
thầy ơi sao không có đề cương ôn tập chương III vậy cho em địa chỉ đó nha

ThíchThích
Trả lời
- caolong | 20/02/2009 lúc 01:15
  Vâng. Để mình soạn xong sẽ upload lên liền. Một thời gian nữa thôi nhé (Tháng 03/2009 sẽ có đủ các chuyên đề)
  
  ThíchThích
  Trả lời
www.vn-seo.com | 20/02/2009 lúc 02:17
Thầy có thể cho em xin giáo trình đó được ko ah?

ThíchThích
Trả lời
- duy | 05/05/2009 lúc 11:38
  thay oi sao ko co them cac pp giai khac va ti mi hon ve he phuong trinh
  
  ThíchThích
  Trả lời
  - caolong | 05/05/2009 lúc 17:01
    Em thông cảm. Hiện thầy đang cố gắng biên soạn một số tài liệu theo chuyên đề để giúp các em ôn tập. Tuy nhiên, do thời gian làm việc nhiều nên chưa rãnh được. Hẹn các em vào một dịp sớm nhất có thể.
    
    ThíchThích
    Trả lời
Le Duy Toan | 11/06/2009 lúc 09:03
Thua thay ,thay co the giai mot so bai tap mot cac ti mi hon ko a!

ThíchThích
Trả lời
Le Duy Toan | 11/06/2009 lúc 09:04
thay giang chung chung rat kho hieu

ThíchThích
Trả lời
- caolong | 11/06/2009 lúc 09:20
  Vâng ! Em có thể gửi một số bài toán mà em thắc mắc. Thầy sẽ định hướng cách giải tĩ mĩ giúp em
  
  ThíchThích
  Trả lời
do thanh duc | 21/06/2009 lúc 07:09
thay oi giup em tinh tick phan tu -pi/4 den pi/4 cua bieu thuc (sin^6x +cos^6x)/(6^x+1) em viet cong thuc toan hoi kem nen thay chiu kho dick ho em $I = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\dfrac{{\sin ^6 x + \cos ^6 x}}{{6^x + 1}}dx}$

ThíchThích
Trả lời
- caolong | 21/06/2009 lúc 07:22
  BÀi này có dạng tổng quát:
  
  Nếu hàm số $f(x)$ là hàm chẵn, liên tục trên đoạn $\left[ { - a;a} \right]$ , khi đó $I=\int\limits_{ - a}^a {\dfrac{{f\left( x \right)}}{{b^x + 1}}dx} = \int\limits_0^a {f\left( x \right)dx}$
  
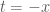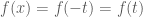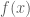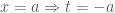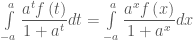  Chứng minh : Đặt $t=-x$ khi đó $dt=-dx$ và $f(x)=f(-t)=f(t)$ do hàm số $f(x)$ là hàm chẵn. Đổi cận: $x=-a \Rightarrow t=a$ ; và $x=a \Rightarrow t=-a$ Ta có $I = \int\limits_a^{ - a} {\dfrac{{f\left( t \right)}}{{b^{ - t} + 1}}\left( { - dt} \right)} = \int\limits_{ - a}^a {\dfrac{{a^t f\left( t \right)}}{{1 + a^t }}dt} = \int\limits_{ - a}^a {\dfrac{{a^x f\left( x \right)}}{{1 + a^x }}dx}$ {Chú ý: Vì tích phân không phụ thuộc vào đối số nên ta có $\int\limits_{ - a}^a {\dfrac{{a^t f\left( t \right)}}{{1 + a^t }}dt} = \int\limits_{ - a}^a {\dfrac{{a^x f\left( x \right)}}{{1 + a^x }}dx}$ } Như vậy $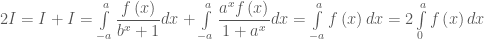2I=I+I=\int\limits_{ - a}^a {\dfrac{{f\left( x \right)}}{{b^x + 1}}dx}+ \int\limits_{ - a}^a {\dfrac{{a^x f\left( x \right)}}{{1 + a^x }}dx} = \int\limits_{ - a}^a {f\left( x \right)dx}=2\int\limits_0^a {f\left( x \right)dx}$ Suy ra $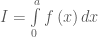I=\int\limits_0^a {f\left( x \right)dx}$ Áp dụng với hàm số $f\left( x \right) = \sin ^6 x + \cos ^6 x$ là hàm số chẵn và liên tục trên đoạn $\left[ { - \dfrac{\pi }{4};\dfrac{\pi }{4}} \right]$ , ta có $I = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\dfrac{{\sin ^6 x + \cos ^6 x}}{{6^x + 1}}dx} = \int\limits_0^{\frac{\pi }{4}} {\left( {\sin ^6 x + \cos ^6 x} \right)dx}$ Em hạ bậc rồi tính tiếp nhé !
  
  ThíchThích
  Trả lời
TRAN BAO KIEU | 06/12/2009 lúc 13:44
thay oi cho em xin hoi the nao la vi phan ? tai sao trong bieu thuc lai co dx ? thay em noi do chi la mot ki hieu chu khong phai phep nhan nhung khi tinh toan thi em lai thay do la mot phep nhan, chang han dt=2xdx suy ra dx=dt/2x ?

ThíchThích
Trả lời
xalem92 | 25/12/2009 lúc 19:07
Em lần đầu tiên vào đây nhưng mạn phép hỏi thầy bài này. Mong thầy giúp em: Nguyên hàm của: e^(sin2x).cosxdx Em cảm ơn!

ThíchThích
Trả lời
xuan son | 08/01/2010 lúc 05:27
em xin thay giup em giai bai nguyen ham nay duoc khong a (x-2)/(x^2+2x+8).em xin cam on thay

ThíchThích
Trả lời
- caolong | 09/01/2010 lúc 00:21
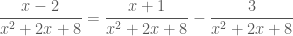
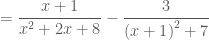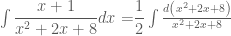
  Có thể phân tích $\dfrac{{x - 2}}{{x^2 + 2x + 8}} = \dfrac{{x + 1}}{{x^2 + 2x + 8}} - \dfrac{3}{{x^2 + 2x + 8}}$ $= \dfrac{{x + 1}}{{x^2 + 2x + 8}} - \dfrac{3}{{\left( {x + 1} \right)^2 + 7}}$ Ta có $\int {\dfrac{{x + 1}}{{x^2 + 2x + 8}}dx = } \dfrac{1}{2}\int {\frac{{d\left( {x^2 + 2x + 8} \right)}}{{x^2 + 2x + 8}}}$ $= \ln \left( {x^2 + 2x + 8} \right) + C_1$ Còn $\int {\dfrac{3}{{\left( {x + 1} \right)^2 + 7}}dx = 3\int {\dfrac{{d\left( {x + 1} \right)}}{{\left( {x + 1} \right)^2 + 7}}} }$ Nguyên hàm này tính được bằng cách đặt $x+1=\sqrt{7} \tan{u}$ Em tự tính tiếp nhé !
  
  ThíchThích
  Trả lời
duc anh | 09/01/2010 lúc 11:34
thay oi sao phan nguyen ham nay truu tuong vay thay

ThíchThích
Trả lời
mai đinh lâp | 14/01/2010 lúc 02:29
em chào thầy a em rất thích wed này of thầy

thầy giải em bài nay nhe’ tìm nguyên hàm của hàm số

căn bậc hai của sinx trên căn bậc hai sinx cộng căn bậc hai của cosx dx em ko biết viết kiểu toán thay thông cảm nhe’

ThíchThích
Trả lời
- caolong | 16/01/2010 lúc 02:00
  Em hỏi bài này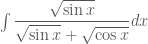 $\int {\dfrac{{\sqrt {\sin x} }}{{\sqrt {\sin x} + \sqrt {\cos x} }}dx}$ phải không ?
  
  ThíchThích
  Trả lời
  - Nghia | 16/04/2012 lúc 14:33
    X=π/2-t =>A=π/4
    
    ThíchThích
    Trả lời
mai đinh lâp | 14/01/2010 lúc 02:31
trang ưed này thật bổ ích em cũng dang tìm 1 trang để ôn

ThíchThích
Trả lời
hocmai_9x_151 | 14/01/2010 lúc 08:03
lam the nao de hoc dc nguyen ham tot day thay sao ma nguyen nay kho vay

ThíchThích
Trả lời
mai đinh lâp | 21/01/2010 lúc 02:18
vâg ạ đúng baì naỳ dâý thâỳ ạ thâỳ giaỉ giùm em tí

ThíchThích
Trả lời
thao ly | 14/02/2010 lúc 11:58
cho e hỏi làm sao chúng ta có thể biết công thức nghiêm horne có nghiệm nào mà để giải

ThíchThích
Trả lời
DG217 | 12/03/2010 lúc 05:50
học nguyên hàm tốt chỉ có 1 cách là làm nhiều hơn nghĩ tự tạo tư duy xác định phương pháp giải ngoài cách đó ra thì chịu .có ai giỏi thì làm bài này nè mấy bài trên bt quá [ cận từ 0 -> 1 căn bận 2 của ( x bình + 1 )dx

ThíchThích
Trả lời
no1_s0nla: | 23/03/2010 lúc 14:52
phan nay sao ma kho the?

ThíchThích
Trả lời
mai dinh lap | 29/03/2010 lúc 15:09
thay oi sao mai ko tha’y thay tra loi vay’ co’ kho’ qua’ ko vay thay`

ThíchThích
Trả lời
Bili_no1 | 03/06/2010 lúc 17:04
Co aj co the chj cho mjnh cach hoc tot fan nguyen ham va tjch fan ko nhj fan nay truu tuog wa mjnh hok hju may

ThíchThích
Trả lời
Nguyễn Lê Hoài | 16/10/2010 lúc 19:57
có ai biết cách giảng phần NGUYÊN HÀM – TÍCH PHÂN một cách dễ hiểu không giảng dùm em y. Em còn mơ hồ vế phần này quá àh. Em không biết cách nào đễ hiểu nó hết trơn ak. Không học được chắc em thi rớt quá àh.

ThíchThích
Trả lời
Lê Hưng | 30/03/2011 lúc 13:06
ai biết cách giảng về phần bài Nguyên hàm – tích phân thì em cảm tạ lắm vì giờ cả đời học Toán em chỉ ngu nhất là phần này mà thôi. Các phần còn lại thì em chỉ cần đi hỏi một tẹo là ra

ThíchThích
Trả lời
bi | 31/10/2011 lúc 22:41
thầy ơi nguyên hàm chỉ có bằng đó kiểu giải đề thôi hả thầy?

ThíchThích
Trả lời
nguyen minh hai | 15/11/2011 lúc 14:30
thua thay! thay co file nao tap hop cac cong thuc toan hoc co ban cua chuong trinh 12 khong? thay co the post len giup em duoc khong thay? em cam on a.

ThíchThích
Trả lời
NGUYEN94(THPT VAn lAM) | 23/11/2011 lúc 21:44
hay the nay ma k pit vao som/.hoho

ThíchThích
Trả lời
huong | 28/06/2012 lúc 01:20
thầy giải hộ em con tích phân này với: tích phan cận từ 0 đến pi/4 của dx/(1+sin^2 (x)). em cám ơn thầy

ThíchThích
Trả lời
- Longeobra | 28/06/2012 lúc 08:52
  $I = \int\limits_0^{\frac{\pi }{4}} {\dfrac{1}{{1 + {{\sin }^2}x}}dx} = \int\limits_0^{\frac{\pi }{4}} {\dfrac{1}{{{{\cos }^2}x\left( {\dfrac{1}{{{{\cos }^2}x}} + \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}} \right)}}dx}$
  
  $I = \int\limits_0^{\frac{\pi }{4}} {\dfrac{1}{{{{\cos }^2}x\left( {1 + 2{{\tan }^2}x} \right)}}dx}$ Đặt $t=tan{x}$ , ta có $dt = \dfrac{1}{\cos^2x}dx$ . $x=0 \Rightarrow t = 0 , \; x= \dfrac{\pi}{4} \Rightarrow t=1$ . Từ đó ta có: $I = \int\limits_0^1 {\dfrac{{dt}}{{1 + 2{t^2}}}}$ Đến đây ta đặt $t=\dfrac{1}{\sqrt{2}}\tan{u}$ $dt= \dfrac{1}{\sqrt{2}} (1+\tan^2 u) du$ Khi $t=0$ ta có $\tan u =0 \Rightarrow u =0$ . Khi $t=1$ ta có $\dfrac{1}{\sqrt{2}}\tan{u} = 1 \Rightarrow \tan u = \sqrt{2} \Rightarrow u = m = \arctan{\sqrt{2}}$ . Và $I = \int\limits_0^m {\dfrac{{1\left( {1 + {{\tan }^2}u} \right)du}}{{\sqrt 2 \left( {1 + {{\tan }^2}u} \right)}} = \dfrac{1}{{\sqrt 2 }}\int\limits_0^m {du} }$ Vậy $I = \left. {\dfrac{1}{{\sqrt 2 }}u} \right|_0^m = \dfrac{m}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}\arctan \sqrt 2$
  
  ThíchThích
  Trả lời
van | 31/12/2012 lúc 19:43
∫▒(X^2+1)/(X^4+X^2+1) dx baì này làm seo thầy

ThíchThích
Trả lời
a | 31/12/2012 lúc 19:49
∫▒x^201/〖(1+x^2)〗^102 dx ∫▒(x^4+1)/(x^6-1) dx ∫▒dx/〖(x^2+1)〗^3

ThíchThích
Trả lời
Lâm Huyền | 15/02/2014 lúc 19:52
thầy ơi giải giúp em con tích phân này: cận từ 0 đến pi/2 (sin3x d(x)/(1+cosx))

ThíchThích
Trả lời

Bình luận về bài viết này Hủy trả lời

Bài viết mới
- Viết pt mặt phẳng qua 3 điểm
- ĐỀ TUYỂN SINH VÀO LỚP 10 THPT THÀNH PHỐ HUẾ NĂM HỌC 2013-2014 (MÔN TOÁN) Xem tại đây.
- Đề kiểm tra học kỳ 1-Toán 12 (Thừa Thiên Huế) Năm học 2012-2013
- Đề tuyển sinh lớp 10 môn Toán năm 2012, Thừa Thiên Huế.
- Đề thi tuyển sinh lớp 10 chuyên Toán Quốc Học, Huế năm 2012
- Đề thi thử đại học số 8 năm 2012- (Tạp chí Toán học tuổi trẻ)
- Đề thi thử đại học số 6 năm 2012 (Toán học tuổi trẻ)
- Đề thi thử đại học môn Toán khối B năm 2012 – Chuyên Quốc học, Huế.
Xem bài theo Chuyên đề
Xem bài theo Chuyên đề Chọn chuyên mục ôn thi đại học (7) Giới thiệu (28) Học tập (3) phần mềm Toán (1) Thông báo KH kiểm tra (4) Tin tức (4) Toán lớp 10 (22) Hình học 10 (3) Đại số 10 (5) Toán lớp 11 (10) GIải tích 11 (4) Hình học KG 11 (1) Lượng giác (1) Toán lớp 12 (36) Giải tích (1) Hình học GT 12 (2) PT Mũ – Lôgarit (2) Số phức (3) Tích phân (4)
Các trang chính
- About me
  - Lời tâm sự
  - Thi giải Toán trên Internet
- BDHSG
  - Chuyên đề phương trình – hệ phương trình
- Geogebra
- Giải đáp
- Học Toán
  - OTDH-P.H.E
    - Cực trị hình học giải tích
    - Giải đề thi thử đại học môn Toán 2010
    - Khảo sát hàm số
    - Nguyên hàm-PP tính
    - Tích phân-Ứng dụng
    - Đề thi lần 1. Lớp PHE
    - Đề thi thử Đại học 2009
      - Giải đề số 08
      - Giải đề số 09
      - Giải đề số 10
      - Giải đề số 11
      - Giải đề só 12
      - Giải đề số 13
      - Giải đề số 14
      - Giải đề số 16
      - Lời giải đề 06
      - Lời giải đề số 07
    - Đường thẳng trong không gian
  - Toán 10
    - BĐT Côsi (Cơ bản)
    - Các bài của học sinh
    - Tam thức bậc hai
    - Đề thi thử hk2, Toán 10
  - Toán 11
    - Giới hạn hàm số
    - Ôn tập chương II (Đại số 11)
    - Ôn tập học kỳ I (Toán 11)
  - Toán 12
    - Bài của học sinh
    - Chuyên đề PT Mũ-Lôgarit
    - Nguyên hàm
    - Phương trình đường thẳng
    - Tọa độ vectơ
    - Đề cương ôn tập học kỳ 1-Toán 12
      - Hướng dẫn giải- Đáp số (Ôn tập Toán 12, học kỳ 1)
    - Đề cương ôn thi Tốt ghiệp
  - Đánh công thức Toán trên Blog wordpress
- Soft
- Tài nguyên
- Toán Blog
Số lượt truy cập
- 1 935 080 lượt
Đang Online
Chào ngày mới
Rank
Giáo dục-Khuyến học (Dân trí)
- Lỗi: có thể dòng không tin đang không hoạt động. Hãy thử lại sau.
Tìm kiếm:
Được đánh giá cao nhất
Liên kết Web
Trường THPT Đặng Trần Côn
Web học tập
- Ôn tập
- Ôn thi
- Blog Vật Lý THPT
- Diễn đàn dạy học Vật lý
- Diễn đàn hóa học phổ thông Hãy đăng ký làm thành viên để tham gia diễn đàn này
- Diễn đàn tóan học
- Học tiếng anh trực tuyến Trang web hỗ trợ bạn tự học tiếng Anh từ dex đến khó
- Học trực tuyến
- Học Vật lý trực tuyến Đăng ký để học và downnload bài tập tham khảo
- hocmai.vn
- Tìm hiểu hóa học Giới thiệu các nghiên cứu, các bài viết hay về hóa học

Ý kiến

	hy trong Đề kiểm tra Hình học 10 (Tham…
	likemath trong Các bước khảo sát hàm số
	likemath trong Các bước khảo sát hàm số
	Lê Văn Hùng trong Giải đề số 2 (Đề thi thử đại h…
	ho thi thu trong Phương trình đường thẳng trong…
	dangloc trong Tính chẵn, lẻ của hàm số
	hatch slack trong Tính chẵn, lẻ của hàm số
	manhhanthtt trong Đề thi tuyển sinh lớp 10 chuyê…
	Khoa trong Đề thi tuyển sinh lớp 10 chuyê…

Blog tại WordPress.com.

Trang này sử dụng cookie. Tìm hiểu cách kiểm soát ở trong: Chính Sách Cookie

Theo dõi Đã theo dõi
- Đỗ Cao Long's Blog.
- Đã có tài khoản WordPress.com? Đăng nhập.
- Đỗ Cao Long's Blog.
- Tùy biến
- Theo dõi Đã theo dõi
- Đăng ký
- Đăng nhập
- URL rút gọn
- Báo cáo nội dung
- Xem toàn bộ bài viết
- Quản lý theo dõi
- Ẩn menu

%d Tạo trang giống vầy với WordPress.comHãy bắt đầu

Từ khóa » Nguyên Hàm Của 1/sinx Dx

Dạy Toán cơ bản cho học sinh yếu môn Toán!

Một số bài toán tìm nguyên hàm.

Ghi nhớ một số nguyên hàm cơ bản:

1.

2.

3.

——————————————-

Bài 1: Tìm nguyên hàm .

Cách 1: Ta phân tích biểu thức dưới dấu nguyên hàm như sau:

Đặt , khi đó nguyên hàm cần tìm được viết lại theo như sau:

Cuối cùng thay ta được:

Cách 2: Dùng công thức góc nhân đôi ta có

Khi đó .

Ta biết

Suy ra

Vậy nguyên hàm đã cho được tính như sau:

.

Chia sẻ:

Bình luận về bài viết này

Comments 36

Bình luận về bài viết này Hủy trả lời

Bài viết mới

Xem bài theo Chuyên đề

Các trang chính

Số lượt truy cập

Đang Online

Chào ngày mới

Rank

Giáo dục-Khuyến học (Dân trí)

Được đánh giá cao nhất

Liên kết Web

Web học tập

Ý kiến

Liên Hệ

1. $\int \dfrac{dx}{x} = \ln |x| +C$

2. $\int \dfrac{dx}{x+a}=\ln|x+a|+C$

3. $\int\dfrac{dx}{ax+b}=\dfrac{1}{a}\int\dfrac{d(ax+b)}{ax+b}$ $= \dfrac{1}{a} \ln|ax+b|+C$