PHÉP SUY ĐỒ THỊ - TaiLieu.VN

Mạng xã hội chia sẻ tài liệu Upload Đăng nhập Nâng cấp VIP Trang chủ » Khoa Học Tự Nhiên » Toán học - Thống kê13 trang 544 lượt xem 180PHÉP SUY ĐỒ THỊ

Kiến thức: Giúp sinh viên hiểu rõ tính chất và nắm được các dạng đồ thị hàm số. Giúp cho sinh viên nắm được các phép suy luận đồ thị (phép đối xứng – phép tịnh tiến). Qua đó giúp sinh viên giảng dạy tốt các nội dung có liên quan trong chương trình toán phổ thông.

Chủ đề:

enter_12

Phép tính vector

Bài giảng Phép tính vector

SaveLikeShareReport Download AI tóm tắt /13BÀI:-8-7-6-5-4-3-2-112345678910-3-2-112345678xyy=f1(x)=2|x|y=f2(x)=|2x-4| A. MC ĐÍCH – YÊU CU:ỤẦ1.Kin thc: ếứ-Giúp sinh viên hiu rõ tính cht và nm đc các dng đ th hàm s.ểấắượạồịố-Giúp cho sinh viên nm đc các phép suy lun đ th (phép đi xng – ắượậồịốứphép tnh tin).ịế-Qua đó giúp sinh viên ging dy tt các ni dung có liên quan trong ảạốộchng trình toán ph thông.ươổ2. K năng:ỹ- Xác đnh đc các phép suy lun đ th.ịượậồị- V đc các dng đ th hàm s.ẽượạồịố- Rèn luyn kĩ năng ra đ kim tra có liên quan đn ni dung này.ệềểếộ3. Thái đ:ộThái đ nghiêm túc, tích cc, ch đng trong hc tp.ộựủộọậ B. NI DUNG:Ộ1Đ TH HÀM S CHA DU ỒỊỐỨẤGIÁ TR TUYT ĐIỊỆỐ2 PHÉP SUY ĐỒ THỊ(PHÉP ĐỐI XỨNG - PHÉP TỊNH TIẾN) Đ xác đnh đ th ca hàm s có cha giá tr tuyt đi (trong ểịồịủốứịệốnhng trng hp khác), thì ta b du giá tr tuyt đi. Khi đó ta ữườợỏấịệốđc hàm s đc cho bi nhiu công thc. Đ th hàm s này ượốượởềứồịốgm nhiu phn, mi phn ng vi đ th ca tng hàm s to ồềầỗầứớồịủừốạthành trên mt tp hp xác đnh. ộậợịLu ý:ư()(), 0yfxfxx==2. Vi ớvà đây là hàm s chn nên đ ốẵồth đi xng qua ịốứOy. Do vy ta có: ậ1. Vi ớ(), ()0()(), ()0fxfxyfxfxfx==−<nên ta có: 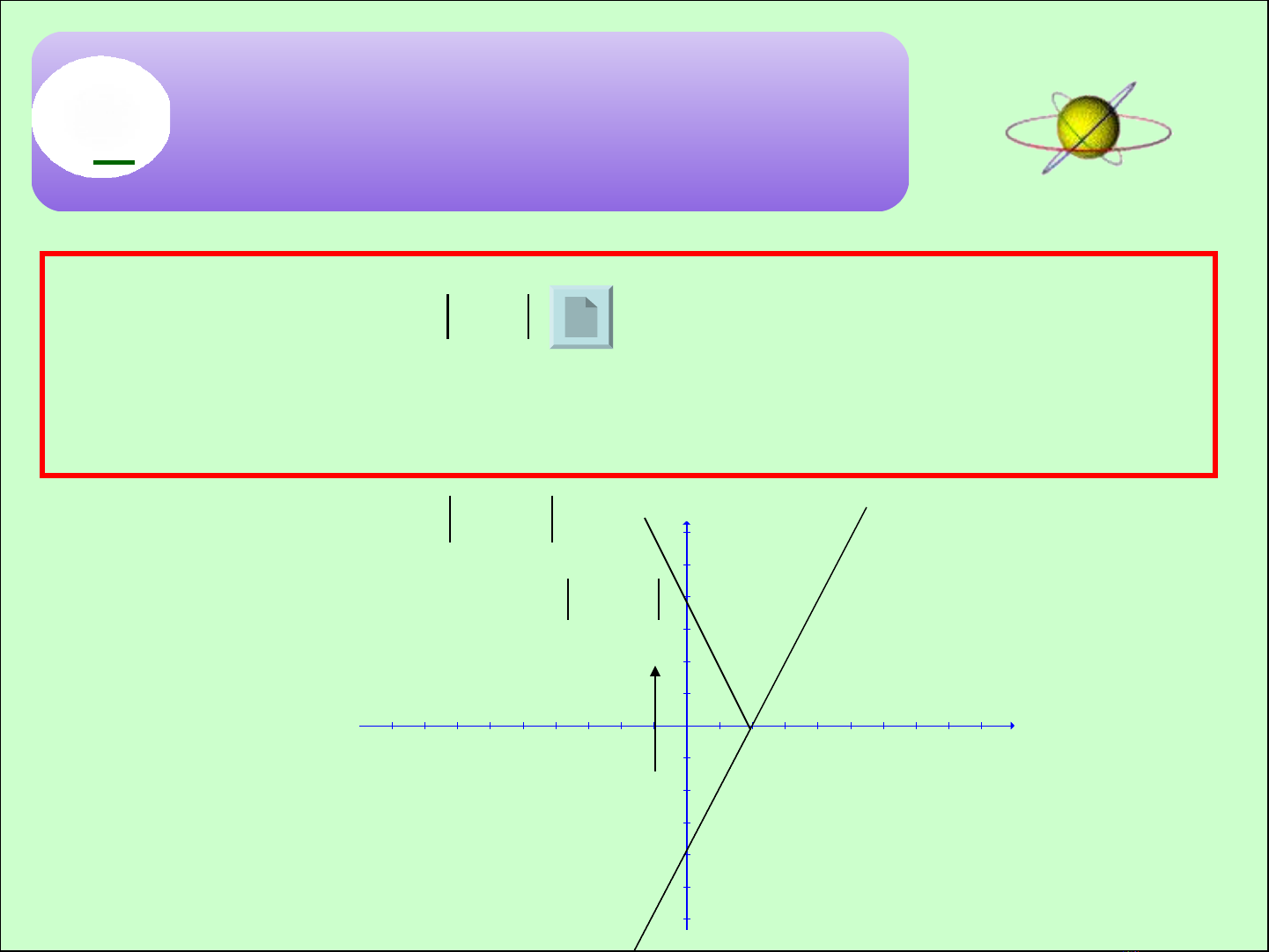1Đ TH HÀM S CHA DU ỒỊỐỨẤGIÁ TR TUYT ĐIỊỆỐ1. Đ th hàm s:ồịố()yfx=Phn 1: Là phn đ th ầầồịy = f(x) ng vi ứớ0yPhn 2: Là phn đi xng qua ầầốứOx ca phn đ th ủầồịy = f(x) ng vi ứớy < 0VD: Đ th hàm s ồịố24yx=−-9-8-7-6-5-4-3-2-1123456789-6-5-4-3-2-1123456xyy=2x-424yx=−Gm hai phn:ồầ

Tài liệu liên quan

Bài giảng Phương pháp tính toán trong khoa học và kỹ thuật vật liệu: Vectơ riêng - giá trị riêng

26 trang

Bài giảng Tích của véc tơ với một số

17 trang

Bài giảng Vector hỗ trợ trong máy học (SVM)

36 trang

Bài giảng Trị riêng - Véctơ riêng - TS. Lê Xuân Đại

75 trang

Bài giảng Không gian véctơ con, tổng và giao của các không gian véctơ con - TS. Lê Xuân Đại

49 trang

Bài giảng Không gian véctơ - TS. Lê Xuân Đại

121 trang

Bài giảng Không gian Euclide - TS. Lê Xuân Đại

53 trang

Bài giảng Toán 1: Bài 4 - Vcbé – Vclớn liên tục (sinh viên) - Nguyễn Quốc Lân

16 trang

Toán cao cấp A1 - Chương 3: Phép tính tích phân của hàm 1 biến

24 trang

Bài thuyết trình Phép biến đổi hình học 3 chiều

47 trang

Tài liêu mới

Bài giảng Hàm một biến thức - ThS. Bùi Thị Ngọc Hân

251 trang

Bài giảng Toán rời rạc - Trần Vĩnh Đức

858 trang

Gợi ý giải bài tập Giải tích III

31 trang

Đề thi kết thúc học phần Cơ sở toán cho các nhà kinh tế 1 (Đề số 07)

12 trang

Đề thi kết thúc học phần Cơ sở toán cho các nhà kinh tế 2 (Đề số 03)

8 trang

Đề thi kết thúc học phần Cơ sở toán cho các nhà kinh tế 1 (Đề số 11)

4 trang

Đề thi kết thúc học phần Cơ sở toán cho các nhà kinh tế 1 (Đề số 02)

24 trang

Bài tập Cơ sở toán Kinh tế 1 (Học kì 1 năm học 2018- 2019)

15 trang

Bài tập ôn tập môn Toán rời rạc

18 trang

Bài tập ôn tập học phần Giải tích 1

12 trang

2 Đề thi kết thúc học phần Toán dành cho kinh tế có lời giải chi tiết năm 2024-2025

9 trang

Đề thi kết thúc học phần Toán dành cho kinh tế và quản trị

2 trang

Đề cương ôn tập môn Xác suất thống kê năm 2023-2024

3 trang

Bài giảng Toán cao cấp: Chương 4 - Một số ứng dụng trong kinh tế

27 trang

Bài giảng Toán cao cấp: Chương 3 - Không gian vecto

33 trang

AI tóm tắt

- Giúp bạn nắm bắt nội dung tài liệu nhanh chóng!

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

Zalo/Tel:

093 303 0098

Email:

[email protected]

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok

Chịu trách nhiệm nội dung: Nguyễn Công Hà Doanh nghiệp quản lý: Công ty TNHH Tài Liệu trực tuyến Vi Na - GCN ĐKDN: 0307893603 Địa chỉ: 54A Nơ Trang Long, P. Bình Thạnh, TP.HCM - Điện thoại: 0283 5102 888 - Email: [email protected]ấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015