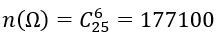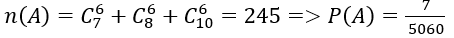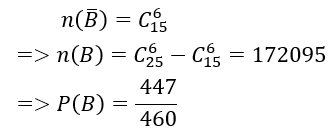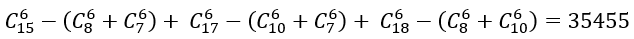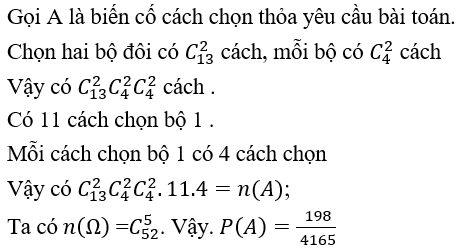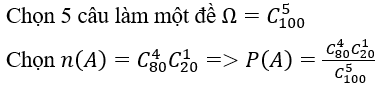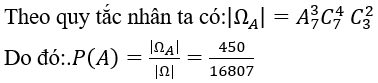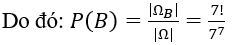Phương Pháp Giải Và Bài Tập Về Cách Tính Xác Suất Theo định Nghĩa ...

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập trắc nghiệm Cách tính xác suất theo định nghĩa cổ điển Toán lớp 11, tài liệu bao gồm 3 trang, tuyển chọn bài tập trắc nghiệm Cách tính xác suất theo định nghĩa cổ điển có phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Cách tính xác suất theo định nghĩa cổ điển gồm các nội dung chính sau:

Phương pháp

- Gồm phương pháp giải Cách tính xác suất theo định nghĩa cổ điển.

Các ví dụ

- Gồm 3 ví dụ minh họa đa dạng của các dạng bài tập Cách tính xác suất theo định nghĩa cổ điển có đáp án và lời giải chi tiết.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

DẠNG 2. CÁCH TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN

Phương pháp:

Tính xác suất theo thống kê ta sử dụng công thức:

So lan xuat hien cua bien co AN.

Tính xác suất của biến cố theo định nghĩa cổ điển ta sử dụng công thức : P(A)=n(A)n(Ω).

Các ví dụ

Ví dụ 1. Bộ bài tú - lơ khơ có 52 quân bài. Rút ngẫu nhiên ra 4 quân bài. Tìm xác suất của các biến cố:

A: “Rút ra được tứ quý K ‘’

A. P(A)=12707 B. P(A)=120725 C. P(A)=170725 D. P(A)=127025

B: “4 quân bài rút ra có ít nhất một con Át”

A. P(B)=1522954145 B. P(B)=12954145 C. P(B)=15954145 D. P(B)=12294145

C: “4 quân bài lấy ra có ít nhất hai quân bích’’

A. P(C)=53920825 B. P(C)=5352085 C. P(C)=53920825 D. P(C)=535920825

Lời giải:

Ta có số cách chọn ngẫu nhiên 4 quân bài là: C524=270725

Suy ra n(Ω)=270725

Vì bộ bài chỉ có 1 tứ quý K nên ta có n(A)=1

Vậy P(A)=1270725.

Vì có C484 cách rút 4 quân bài mà không có con Át nào,

suy ra N(b)=C524−C484 ⇒P(B)=1522954145.

Vì trong bộ bài có 13 quân bích, số cách rút ra bốn quân bài mà trong đó số quân bích không ít hơn 2 là: C132.C392+C133C391+C134.C390=69667

Suy ra n(C)=69667⇒P(C)=535920825.

Ví dụ 2. Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. Tìm xác suất để:

1. 3 viên bi lấy ra đều màu đỏ

A. P(A)=14285 B. P(A)=4285 C. P(A)=1425 D. P(A)=1285

2. 3 viên bi lấy ra có không quá hai màu.

A. P(B)=37 B. P(B)=4357 C. P(B)=457 D. P(B)=357

Lời giải:

Gọi biến cố A :“ 3 viên bi lấy ra đều màu đỏ”

B : “3 viên bi lấy ra có không quá hai màu”

Số các lấy 3 viên bi từ 20 viên bi là: C203 nên ta có: Ω=C203=1140

1. Số cách lấy 3 viên bi màu đỏ là: C83=56 nên ΩA=56

Do đó: P(A)=ΩAΩ=561140=14285.

2. Ta có:

Số cách lấy 3 viên bi chỉ có một màu: C83+C73+C53=101

Số các lấy 3 viên bi có đúng hai màu

Đỏ và xanh: C153−C83+C73

Đỏ và vàng: C133−C83+C53

Vàng và xanh: C123−C53+C73

Nên số cách lấy 3 viên bi có đúng hai màu:

C153+C133+C123−2C83+C73+C53=759

Do đó: ΩB=860. Vậy P(B)=ΩBΩ=4357.

Ví dụ 3. Chọn ngẫu nhiên 3 số trong 80 số tự nhiên 1,2,3, . . . ,80

1. Tính xác suất của biến cố A : “trong 3 số đó có và chỉ có 2 số là bội số của 5”

A. n(A)=96127 B. n(A)=61027 C. n(A)=96107 D. n(A)=961027

2. Tính xác suất của biến cố B : “trong 3 số đó có ít nhất một số chính phương”

A. n(B)=53254 B. n(B)=56205 C. n(B)=5632054 D. n(B)=53204

Bài tập vận dụng

Bài 1:Gieo con súc sắc 100 lần, kết quả thu được ghi ở bảng sau

Số chấm	Số lần xuất hiện
1	14
2	18
3	30
4	12
5	14
6	12

Hãy tìm xác suất của các biến cố

A: "mặt sáu chấm xuất hiện"

B: " mặt hai chấm xuất hiện"

C: " một mặt lẻ xuất hiện"

Lời giải:

Xem việc tung con súc sắc là một phép thử ngẫu nhiên

Số lần thực hiện phép thử: N=100

Số lần xuất hiện của biến cố A: 12

Suy ra : P(A)= 12/ 100= 3/ 25

Số lần xuất hiện của biến cố B: 18

Suy ra P(B)= 18/ 100= 9/ 50

Số lần xuất hiện của biến cố C:

Suy ra P(C)= 58/ 100= 29/ 50.

Bài 2:Trong một chiếc hộp có 7 viên bi trắng, 8 viên bi đỏ và 10 viên bi vàng. Lấy ngẫu nhiên ra 6 viên bi

1.Tính số phần tử của không gian mẫu

2.Tính xác suất của các biến cố sau

A: " 6 viên bi lấy ra cùng một màu"

B: " có ít nhất một viên bi màu vàng"

C: " 6 viên bi lấy ra có đủ ba màu"

Lời giải:

1.Ta có:

2.Ta có:

Ta có:

Ta có: Số cách lấy 6 viên bi cùng một màu: 245 cách

Số cách lấy 6 viên bi gồm hai màu:

Suy ra n(C)=177100-35455-245=141400. Vậy P(C)=202/253.

Bài 3:Chọn ngẫu nhiên 5 quân bài trong cỗ bài tú lơ khơ .Tính xác suất để trong sấp bài chứa hai bộ đôi ( hai con cùng thuộc 1 bộ ,hai con thuộc bộ thứ 2,con thứ 5 thuộc bộ khác )

Lời giải:

Bài 4:Ngân hàng đề thi gồm 100 câu hỏi, mỗi đề thi có 5 câu. Một học sinh học thuộc 80 câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có 4 câu học thuộc.

Lời giải:

Bài 5:Một đoàn tàu có 7 toa ở một sân ga. Có 7 hành khách từ sân ga lên tàu, mỗi người độc lập với nhau và chọn một toa một cách ngẫu nhiên. Tìm xác suất của các biến cố sau

A: " Một toa 1 người, một toa 2 người, một toa có 4 người lên và bốn toa không có người nào cả"

B: " Mỗi toa có đúng một người lên".

Lời giải:

Số cách lên toa của 7 người là:.|Ω|=77

1.Tính P(A)=?

Ta tìm số khả năng thuận lợi của A như sau

2.Tính P(B)=?

Mỗi một cách lên toa thỏa yêu cầu bài toán chính là một hoán vị của 7 phần từ nên ta có: |ΩB|=7!

Xem thêm