Phương Pháp Giải Và Tính Nhẩm Nghiệm Phương Trình Bậc 2

Cần phải có phương pháp giải và tính nhẩm nghiệm phương trình bậc 2 thật chính xác để làm bước khởi đầu tiến sâu vào tam thức bậc 2 và các bài toán liên quan khác.

• Những lưu ý quan trọng khi ôn thi vào lớp 10 môn Toán
• 5 bí quyết “vàng” luyện thi trắc nghiệm môn Toán
• Làm thế nào để ôn thi môn Toán THPT Quốc gia hiệu quả chỉ với 2h mỗi ngày?

Nếu trong quá trình học tập, học sinh vẫn chưa hiểu rõ về cách giải phương trình bậc 2, hãy cùng chúng tôi tham khảo và tìm hiểu cách giải chi tiết và cách tính nhẩm nghiệm phương trình bậc 2 trong bài viết chia sẻ dưới đây nhé!

• Tổng hợp: Các dạng bài tập toán phương trình và hệ phương trình
• Tổng hợp: Bài tập về bất đẳng thức – GTLN – GTNN của biểu thức
• Phương pháp chứng minh tính chẵn, lẻ của hàm số – Đại số 10
• Giới thiệu về Parabol và ứng dụng
• Tổng hợp: Các dạng bài tập chuyên đề hàm số bậc nhất và bậc hai

Tóm tắt

• 1 Phương trình bậc 2 là gì?
• 2 Phương pháp giải phương trình bậc 2
  • 2.1 Định lý Vi-ét
  • 2.2 Một số trường hợp đặc biệt
• 3 Cách tính nhẩm nghiệm phương trình bậc 2
  • 3.1 Dạng 1: A = 1, B = Tổng, C = Tích
  • 3.2 Dạng 2: A + B + C = 0 và A – B + C = 0
  • 3.3 Dạng 3: Hai nghiệm là nghịch đảo của nhau
• 4 Một số ví dụ vận dụng

Phương trình bậc 2 là gì?

Phương trình bậc hai là phương trình có dạng: ax2 + bx + c = 0. Với

• x là ẩn số
• a, b, c là các số đã biết sao cho: a ≠ 0
• a, b, c là những hệ số của phương trình và có thể phân biệt bằng cách gọi tương ứng với hệ số của x (theo phương trình trên thì a là hệ số bậc hai, b là hệ số bậc một, c là hằng số hay số hạng tự do).

Phương pháp giải phương trình bậc 2

Giải phương trình bậc 2: ax2 + bx + c = 0 theo biệt thức delta (Δ)

Định lý Vi-ét

Công thức Vi-ét về quan hệ giữa các nghiệm của đa thức với các hệ số của nó. Trong trường hợp phương trình bậc hai một ẩn, được phát biểu như sau:

Một số trường hợp đặc biệt

Nếu phương trình bậc 2 có:

Cách tính nhẩm nghiệm phương trình bậc 2

Giảng viên Trường Trung học phổ thông Sài Gòn chia sẻ: Xuất phát từ định lý Vi-ét, chúng ta có các dạng toán tính nhẩm như sau:

Dạng 1: A = 1, B = Tổng, C = Tích

Nếu phương trình có dạng x2 – (u+v)x + uv = 0 thì phương trình đó có hai nhiệm u và v.

Nếu phương trình có dạng x2 + (u+v)x + uv = 0 thì phương trình có hai nghiệm -u và –v.

Tóm lại:

• x2 – (u+v)x + uv = 0 => x1 = u, x2 = v (1)
• x2 + (u+v)x + uv = 0 => x1 = -u, x2 = -v

Như vậy, với dạng này chúng ta cần thực hiện 2 phép nhẩm: “Phân tích hệ số c thành tích và b thành tổng”. Trong hai phép nhẩm đó, chúng ta nên nhẩm hệ số c trước rồi kết hợp với b để tìm ra hai số thỏa mãn tích bằng c và tổng bằng b.

Khi tiến hành, bạn nhẩm trong đầu như sau: Tích của hai nghiệm bằng c, mà tổng lại bằng b.

Ví dụ phương trình:

1. x2 – 5x + 6 = 0

Nhẩm: “Tích của hai nghiệm bằng 6, mà tổng lại bằng 5”. Hai số đó là: 2 và 3 vì 6 = 2×3 và 5 = 2 + 3. Vậy phương trình có hai nghiệm x = 2, x = 3.

1. x2 – 7x + 10 = 0

Nhẩm: “Tích của hai nghiệm bằng 10, mà tổng lại bằng 7”. Hai số đó là: 2 và 5 vì 10 = 2×5 và 7 = 2 + 5. Vậy phương trình có hai nghiệm x = 2, x = 5.

Dạng 2: A + B + C = 0 và A – B + C = 0

x2 – (u+v)x + uv = 0 => x1 = u, x2 = v (1)

• Nếu thay v = 1 vào (1) thì chúng ta sẽ có trường hợp nhẩm nghiệm quen thuộc a + b + c = 0, với a = 1, b = -(u+1), c = u.
• Nếu thay v = -1 vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm a – b + c = 0, với a = 1, b = -(u-1), c = -u.

Do loại này đã quá quen thuộc và thường gặp, nên bài viết không xét các ví dụ cho trường hợp này mà tập trung vào Dạng 1 và Dạng 3.

Dạng 3: Hai nghiệm là nghịch đảo của nhau

Nếu u ≠ 0 và v = 1/u thì phương trình (1) có dạng:

Khi đó: Phương trình có hai nghiệm là nghịch đảo của nhau x= u, x = 1/u. Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình:

• 2x2 – 5x + 2 = 0 có hai nghiệm x = 2, x = 1/2
• 3x2 – 10x + 3 = 0 có hai nghiệm x = 3, x = 1/3

Một số ví dụ vận dụng

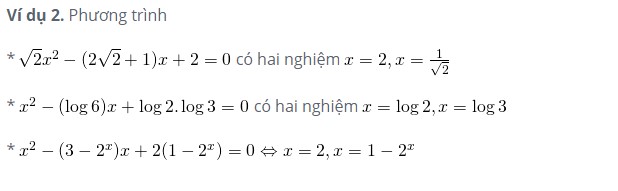
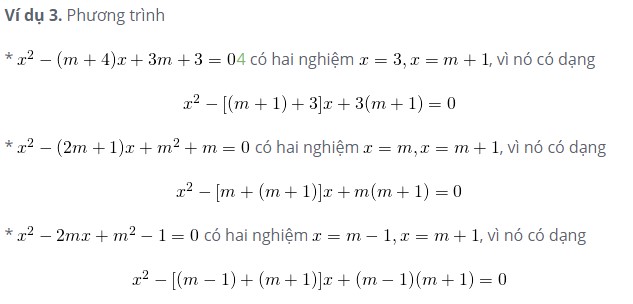
Dựa vào đó, các bạn hãy áp dụng và thử giải các bài tập sau đây nhé:

1. 2x2 + 6x + 5 = 0
2. x2 – 4x + 4 = 0
3. 2x2 + 7x – 3 = 0.

Khi mới làm quen với tính nhẩm, có thể chúng ta sẽ gặp một chút khó khăn, nhưng đừng vì thế mà ngại khó và bỏ cuộc. Hãy tưởng tượng thành quả mà phương pháp tính nhẩm đem lại cho chúng ta là “không đếm được” so với những “trở ngại đếm được” mà bạn đang phải đối mặt. Chúng ta sẽ có thêm động lực tiến lên.

Nguồn: Toancap3.com tổng hợp