Phương Pháp Và Bài Tập Tính Nguyên Hàm Từng Phần
Có thể bạn quan tâm
T. LÝ THUYẾT
1. Định lý.
Nếu u = (x) và v = v(x) là 2 hàm số có đạo hàm liên tục trên đoạn K thì:
\(\int u(x)v'(x)dx=u(x).v(x)-u(x)\int v(x)dx\)
Viết gọn lại: \(\int udv=u.v-v\int du\)
2. Một số dạng tính nguyên hàm từng phân.
Dạng 1: \(I = \int {f\left( x \right)\sin xdx} \) hoặc \(I = \int {f\left( x \right)\cos xdx} \), trong đó f(x) là đa thức.
Phương pháp: Đặt \(\left\{\begin{matrix} u=f(x) & \\ dv=sinxdx & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} du=f'(x)dx & \\ v=\int sinxdx& \end{matrix}\right.\)
Dạng 2: \(I=\int f(x).e^{x}dx\) , trong đó f(x) là 1 đa thức.
Phương pháp: Đặt \(\left\{\begin{matrix} u=f(x) & \\ dv=e^{x}dx & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} du=f'(x)dx & \\ v=\int e^{x}dx& \end{matrix}\right.\)
Dạng 3: \(I = \int {f\left( x \right)\ln xdx} \) hoặc \(I = \int {f\left( x \right){{\log }_a}xdx} \), trong đó f(x) là 1 đa thức.
Phương pháp: Đặt: \(\left\{\begin{matrix} u=lnx & \\ dv=f(x)dx & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} du=\frac{1}{x} dx& \\ v=\int f(x) dx& \end{matrix}\right.\)
3. Một số chú ý:
Khi gặp lượng giác và mũ ta có thể đặt “u→dv” theo thứ tự “lượng giác → mũ” hoặc ngược lại đều được và phải sử dụng hai lần tích phân từng phần. Cả hai lần tích phân từng phần trong trường hợp nàyphải thống nhất theo cùng thứ tự. Nếu không sẽ xảy ra hiện tượng I = I.+) Khi sử dụng phương pháp tích phân từng phần thì số lần thực hiện phụ thuộc vào bậc của hàm logarit và đa thức. Cụ thể:*) Nếu trong biểu thức tích phân có \(log_{n}^{a} f(x) ; ln^{n}f(x)\) thì phải tích phân từng phần n lần.*) Nếu trong biểu thức tích phân có đa thức bậc n: (không có hàm logarit) ==> thì cũng phải tích phân từng phần lần.
II. LUYỆN TẬP.
Ví dụ 1. Tìm nguyên hàm của các hàm số sau:
\(a)I_{1}=\int x.sinxdx; b) I_{2}=\int x.e^{3x}dx; c)\int x^{2}.cosxdx\)
Hướng dẫn giải
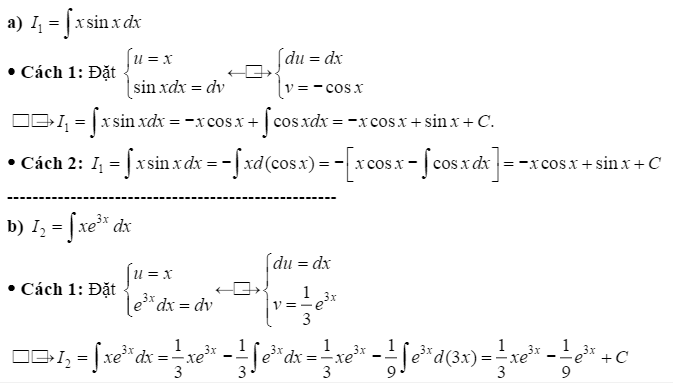
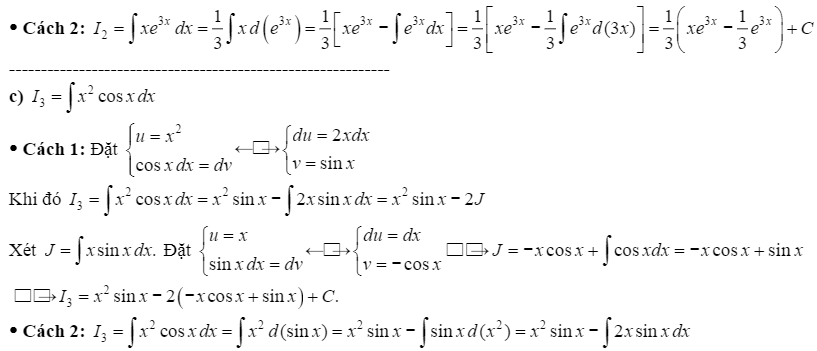
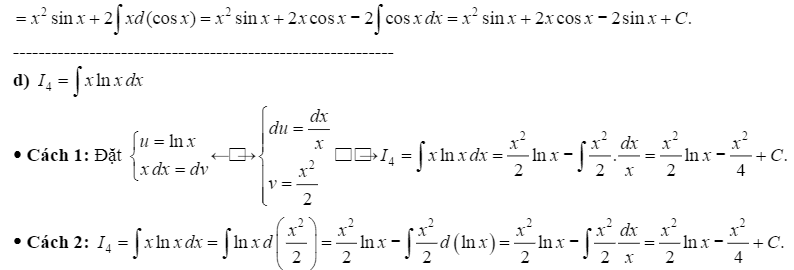

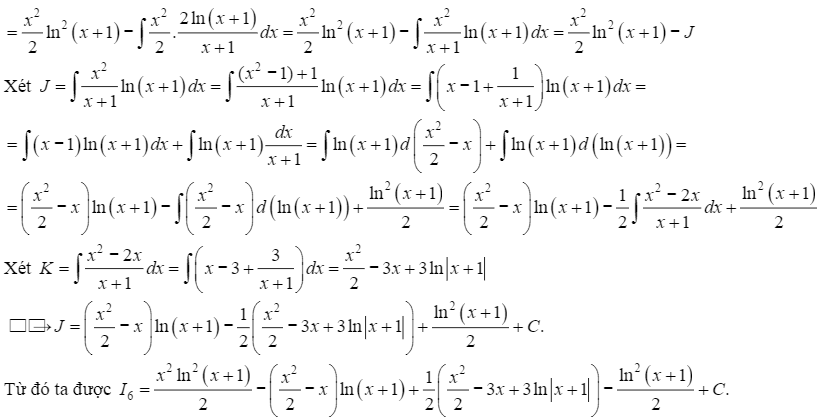
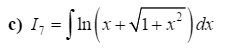
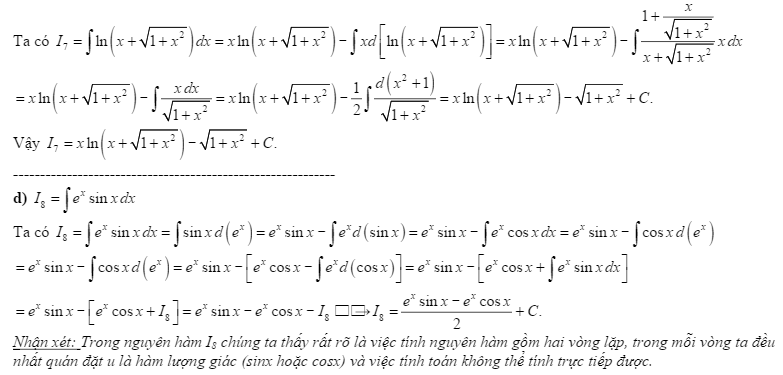
BÀI TẬP TỰ LUYỆN

Từ khóa » đặt Udv
-
Công Thức Tính Nguyên Hàm Từng Phần Và Cách Giải Bài Tập
-
Công Thức Nguyên Hàm Từng Phần đầy đủ Nhất - Top Lời Giải
-
Phương Pháp Nguyên Hàm Từng Phần, Trắc Nghiệm Toán Học Lớp 12
-
Công Thức Nguyên Hàm Udv
-
Phương Pháp Và Công Thức Tính Nguyên Hàm Từng Phần - Icongchuc
-
Công Thức Nguyên Hàm Từng Phần - Tính Nhanh Bằng Sơ đồ
-
Tìm Nguyên Hàm Bằng Phương Pháp Nguyên Hàm Từng Phần
-
Phương Pháp Và Bài Tập Tính Nguyên ... - .vn
-
Tích Phân Từng Phần, Công Thức Cách Tính Và Bài Tập Có Lời Giải
-
Tích Phân Từng Phần - SlideShare
-
Chi Tiết Công Thức Tính Nguyên Hàm Từng Phần Cơ Bản Và Nâng Cao
-
Hướng Dẫn Giải Bài Tập Toán Đại 12: Chương Nguyên Hàm Chọn ...
-
Công Thức Nguyên Hàm Từng Phần Và Cách Giải Bài Tập Chi Tiết