Phương Trình Bậc 2 Một ẩn Là Gì? Ví Dụ Về Giải Phương Trình Bậc Hai ...
Có thể bạn quan tâm
Để giải bài toán như này, chúng ta sẽ cùng tìm hiểu về phương trình bậc 2 một ẩn là gì? qua đó giải một số ví dụ về phương trình bậc 2 một ẩn để các em dễ hiểu qua bài viết dưới đây.
1. Phương trình bậc 2 một ẩn là gì?
* Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng:
ax2 + bx + c = 0
Trong đó: x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.
* Ví dụ: Các phương trình sau là phương trình bậc 2
x2 + 30x - 55 = 0 là phương trình bậc hai với các hệ số a = 1; b = 30; c = -55.
-3x2 + 7x = 0 là phương trình bậc hai với các hệ số a = -3; b = 7; c = 0.
2x2 - 9 = 0 là phương trình bậc 2 với các hệ số a = 2; b = 0; c = -9.
2. Một số ví dụ về giải phương trình bậc hai
* Ví dụ 1: Giải phương trình bậc hai: 2x2 + 5x = 0
* Lời giải:
- Ta có: 2x2 + 5x = 0 ⇔ x(2x + 5) = 0 ⇔ x = 0 hoặc 2x + 5 = 0
⇔ x = 0 hoặc x = -5/2.
Vậy phương trình có nghiệm x = 0 hoặc x = -5/2.
* Ví dụ 2: Giải phương trình bậc hai: 3x2 - 2 = 0.
* Lời giải:
- Ta có: 3x2 - 2 = 0 ⇔ 3x2 = 2 ⇔ x2 = 2/3
tức là 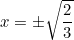
Vậy phương trình có hai nghiệm: 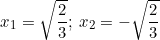
* Ví dụ 3: Giải phương trình bậc 2 sau: (x - 2)2 = 7/2.
* Lời giải:
- Ta có: 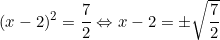
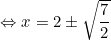
Vậy phương trình có 2 nghiệm: 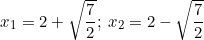
* Ví dụ 4: Giải phương trình bậc 2 sau: x2 – 4x + 4 = 7/2
* Lời giải:
- Ta có: x2 - 4x + 4 = 7/2 ⇔ (x - 2)2 = 7/2
⇔ x - 2 = ±√(7/2) ⇔ x = 2 ± √(7/2)
Vậy phương trình có hai nghiệm: 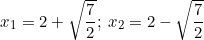
* Ví dụ 5: Giải phương trình bậc 2 sau: x2 – 4x = -1/2.
* Lời giải:
x2 - 4x = -1/2 ⇔ x2 - 4x + 4 = -1/2 + 4 ⇔ (x - 2)2 = 7/2
⇔ x - 2 = ±√(7/2) ⇔ x = 2±√(7/2)
Vậy phương trình có hai nghiệm: 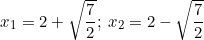
* Ví dụ 6: Giải phương trình bậc hai: 2x2 – 8x = -1
* Lời giải:
- Ta có: 2x2 - 8x = -1 ⇔ x2 - 4x = (-1)/2
⇔ x2 - 4x + 4 = (-1)/2 + 4 ⇔ (x - 2)2=7/2
⇔ x - 2 = ±√(7/2) ⇔ x = 2 ±√(7/2)
Vậy phương trình có hai nghiệm: x1 = 2 + √(7/2); x2 = 2 - √(7/2)
3. Bài tập vận dụng
* Bài 11 trang 42 SGK Toán 9 Tập 2: Đưa các phương trình sau về dạng ax2 + bx + c = 0 và chỉ rõ các hệ số a, b, c:
a) 5x2 + 2x = 4 - x
b)
c) 2x2 + x - √3 = x.√3 + 1
d) 2x2 + m2 = 2(m - 1)x, (m là một hằng số)
* Lời giải:
a) 5x2 + 2x = 4 – x
⇔ 5x2 + 2x + x – 4 = 0
⇔ 5x2 + 3x – 4 = 0
Phương trình bậc hai trên có a = 5; b = 3; c = -4.
b)
⇔ 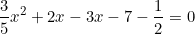
⇔ 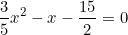
Phương trình bậc hai trên có a = 3/5; b = -1; c = -15/2.
c) 2x2 + x - √3 = x.√3 + 1
⇔ 2x2 + x - x.√3 - √3 – 1 = 0
⇔ 2x2 + (1 - √3)x – (√3 + 1) = 0
Phương trình bậc hai trên có a = 2; b = (1 - √3); c = - (√3 + 1).
d) 2x2 + m2 = 2(m – 1).x
⇔ 2x2 – 2(m – 1).x + m2 = 0
Phương trình bậc hai trên có a = 2; b = -2(m – 1); c = m2.
* Bài 12 trang 42 SGK Toán 9 Tập 2: Giải các phương trình sau:
a) x2 – 8 = 0; b) 5x2 – 20 = 0;
c) 0,4x2 + 1 = 0 d) 2x2 + √2x = 0;
e) -0,4x2 + 1,2x = 0.
* Lời giải:
a) x2 – 8 = 0 ⇔ x2 = 8
⇔ x = 2√2 hoặc x = -2√2.
Vậy phương trình có hai nghiệm x = 2√2 và x = -2√2.
b) 5x2 – 20 = 0
⇔ 5x2 = 20 ⇔ x2 = 4
⇔ x = 2 hoặc x = -2.
Vậy phương trình có hai nghiệm x = 2 và x = -2.
c) 0,4x2 + 1 = 0
⇔ 0,4x2 = -1 ⇔ x2 = -10/4
Phương trình vô nghiệm vì x2 ≥ 0 với mọi x.
d) 2x2 + x√2 = 0
⇔ x√2.(x√2 + 1) = 0
⇔ x = 0 hoặc x√2 + 1 = 0
⇔ x = 0 hoặc x = -1/√2
Vậy phương trình có hai nghiệm x = 0 và x = -1/√2.
e) -0,4x2 + 1,2x = 0
⇔ -0,4x.(x – 3) = 0
⇔ x = 0 hoặc x – 3 = 0
⇔ x = 0 hoặc x = 3
Vậy phương trình có hai nghiệm x = 0 và x = 3.
* Bài 13 trang 43 SGK Toán 9 Tập 2: Cho các phương trình:
a) x2 + 8x = -2
b) x2 + 2x = 1/3
Hãy cộng vào hai vế của mỗi phương trình cùng một số thích hợp để được một phương trình mà vế trái thành một bình phương.
* Lời giải:
a) x2 + 8x = -2
⇔ x2 + 2.x.4 + 42 = -2 + 42
⇔ (x + 4)2 = 14
b) x2 + 2x = 1/3
⇔ x2 + 2x + 1 = 1/3 + 1
⇔ (x + 1)2 = 4/3.
* Bài 14 trang 43 SGK Toán 9 Tập 2: Hãy giải phương trình : 2x2 + 5x + 2 = 0 theo các bước như ví dụ 3 trong bài học.
* Lời giải:
- Ta có: 2x2 + 5x + 2 = 0
⇔ 2x2 + 5x = -2 (chuyển 2 sang vế phải)
⇔ 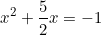 (chia cả 2 vế cho 2)
(chia cả 2 vế cho 2)
⇔ 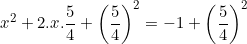
(Tách (5/2)x thành 2.x.(5/4) và cộng thêm (5/4)2 vào 2 vế để vế trái xuất hiện thành bình phương dạng (a + b)2 = a2 + 2.a.b + b2).
⇔ 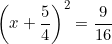
⇔ x + 5/4 = 3/4 hoặc x + 5/4 = -3/4
⇔ x = -1/2 hoặc x = -2.
Vậy phương trình có hai nghiệm: x1 = -1/2; x2 = -2.
Từ khóa » Cách Tính Phương Trình Bậc 2 Một ẩn
-
Tổng Hợp Dạng Toán Về Phương Trình Bậc 2 Một ẩn Thông Dụng Nhất.
-
Phương Trình Bậc 2 Một ẩn Và Cách Giải đúng Bạn Cần Biết
-
Phương Trình Bậc Hai Một ẩn: Lý Thuyết Và Cách Giải Các Dạng Toán
-
Cách Giải Phương Trình Bậc 2 Một ẩn - TopLoigiai
-
Phương Trình Bậc Hai Một ẩn Và Cách Giải - YouTube
-
Cách Giải Phương Trình Bậc 2 Một Ẩn Số, Ví Dụ Về ...
-
Phương Pháp Giải Phương Trình Bậc Hai Một ẩn Hay, Chi Tiết
-
Cách Giải Phương Trình Bậc 2 - Gia Sư Tâm Tài Đức
-
3 Cách Giải Phương Trình Bậc 2 Cực đơn Giản, Chính Xác 100%
-
Phương Trình Bậc Hai Một ẩn Và Công Thức Nghiệm
-
Cách Giải Phương Trình Bậc Hai Nhanh Nhất - Học Toán Lớp 9
-
Công Thức Nghiệm Của Phương Trình Bậc Hai
-
Cách Giải Phương Trình Bậc 2
-
Phương Pháp Học Sinh Phải Biết để Giải Phương Trình Bậc 2 Một ẩn