Tam Giác đều – Wikipedia Tiếng Việt
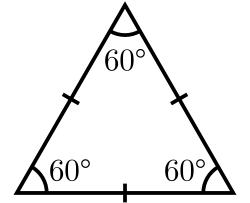
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.
Tính chất
[sửa | sửa mã nguồn]Giả sử độ dài ba cạnh tam giác đều bằng , dùng định lý Pytago chứng minh được:
- Diện tích:
- Chu vi:
- Bán kính đường tròn ngoại tiếp
- Bán kính đường tròn nội tiếp
- Trọng tâm của tam giác cũng là trực tâm và tâm của đường tròn nội tiếp và ngoại tiếp
- Chiều cao của tam giác đều .
Với một điểm P bất kỳ trong mặt phẳng tam giác, khoảng cách từ nó đến các đỉnh A, B, và C lần lượt là p, q, và t ta có:[1]
.Với một điểm P bất kỳ nằm bên trong tam giác, khoảng cách từ nó đến các cạnh tam giác là d, e, và f, thì d+e+f = chiều cao của tam giác, không phụ thuộc vào vị trí P.[2]
Với điểm P nằm trên đường tròn ngoại tiếp, các khoảng cách từ nó đến các đỉnh của tam giác là p, q, và t, thì[1]
và
.Nếu P nằm trên cung nhỏ BC của đường tròn ngoại tiếp, với khoảng cách đến các đỉnh A, B, và C lần lượt là p, q, và t, ta có:[1]
và
hơn nữa nếu D là giao điểm của BC và PA, DA có độ dài z và PD có độ dài y, thì[3]
và cũng bằng nếu t ≠ q; và
Dấu hiệu nhận biết
[sửa | sửa mã nguồn]- Tam giác có 3 cạnh bằng nhau là tam giác đều.
- Tam giác có 3 góc bằng nhau là tam giác đều.
- Tam giác cân có một góc bằng 60° là tam giác đều.
- Tam giác có 2 góc bằng 60 độ là tam giác đều.
- Tam giác có đường cao bằng nhau hoặc 3 đường phân giác bằng nhau hoặc 3 đường trung tuyến bằng nhau thì tam giác đó là tam giác đều.
- Tam giác có 2 trong 4 điểm đồng quy (trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp) trùng nhau thì tam giác đó là tam giác đều
Xem thêm
[sửa | sửa mã nguồn]- Lượng giác
- Định lý Viviani
- Tam giác Heron
Tham khảo
[sửa | sửa mã nguồn]- ^ a b c De, Prithwijit, "Curious properties of the circumcircle and incircle of an equilateral triangle," Mathematical Spectrum 41(1), 2008-2009, 32-35.
- ^ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover Publ., 1996.
- ^ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, second edition, Dover Publ. Co., 1996, pp. 170-172.
Liên kết ngoài
[sửa | sửa mã nguồn]- Weisstein, Eric W., "Equilateral Triangle", MathWorld.
Từ khóa » Cm Tg đều
-
Nêu 3 Cách Chứng Minh Tam Giác Cân Tam Giác đều - Nguyễn Thị An
-
Cách Chứng Minh Tam Giác đều Là Tam Giác Cân - TopLoigiai
-
Các Cách Chứng Minh Tam Giác đều
-
Định Nghĩa, Tính Chất & Cách Chứng Minh Các Tam Giác đặc Biệt
-
Cách Tính đường Cao Tam Giác đều - Thủ Thuật Phần Mềm
-
[Toán 9] Chứng Minh Tam Giác ABC đều. | Bài Tập Toán THCS
-
Công Thức Tính đường Cao Trong Tam Giác Thường, Cân, đều, Vuông
-
TAM GIÁC ĐỀU: Định Nghĩa, Tính Chất, Công Thức Và Dấu Hiệu Nhận ...
-
Công Thức Tính Diện Tích Tam Giác: đều, Cân, Vuông, Thường Từ A - Z
-
Tam Giác đều Là Gì ? Định Nghĩa, Tính Chất Về Tam Giác đều Chi Tiết
-
Định Nghĩa, Tính Chất, Cách Chứng Minh Tam Giác đều - Abcdonline
-
Nêu Cách Chứng Minh Và Tính Chất Của Nửa Tam Giác đều
-
Tính độ Dài Cạnh Của Tam Giác đều Nội Tiếp (( (O;R) ) ) Theo (R
-
Lý Thuyết Tam Giác Cân | SGK Toán Lớp 7













