Tam Thức Bậc Hai | Đỗ Cao Long's Blog.
Có thể bạn quan tâm
- Bỏ qua điều hướng
- Chuyển đến nội dung chính
- Skip to primary sidebar
- Skip to secondary sidebar
- Skip to footer
Dạy Toán cơ bản cho học sinh yếu môn Toán!
- Trang chủ
- About me
- Thi giải Toán trên Internet
- Lời tâm sự
- BDHSG
- Chuyên đề phương trình – hệ phương trình
- Geogebra
- Giải đáp
- Học Toán
- Toán 10
- Đề thi thử hk2, Toán 10
- BĐT Côsi (Cơ bản)
- Tam thức bậc hai
- Các bài của học sinh
- Đánh công thức Toán trên Blog wordpress
- Toán 11
- Ôn tập chương II (Đại số 11)
- Ôn tập học kỳ I (Toán 11)
- Giới hạn hàm số
- Toán 12
- Bài của học sinh
- Chuyên đề PT Mũ-Lôgarit
- Nguyên hàm
- Phương trình đường thẳng
- Đề cương ôn tập học kỳ 1-Toán 12
- Hướng dẫn giải- Đáp số (Ôn tập Toán 12, học kỳ 1)
- Tọa độ vectơ
- Đề cương ôn thi Tốt ghiệp
- OTDH-P.H.E
- Cực trị hình học giải tích
- Giải đề thi thử đại học môn Toán 2010
- Nguyên hàm-PP tính
- Khảo sát hàm số
- Đề thi thử Đại học 2009
- Giải đề số 10
- Giải đề số 11
- Giải đề só 12
- Giải đề số 13
- Giải đề số 16
- Giải đề số 08
- Giải đề số 09
- Giải đề số 14
- Lời giải đề 06
- Lời giải đề số 07
- Tích phân-Ứng dụng
- Đề thi lần 1. Lớp PHE
- Đường thẳng trong không gian
- Toán 10
- Soft
- Tài nguyên
- Toán Blog
DẤU CỦA TAM THỨC BẬC HAI VÀ ỨNG DỤNG
Định lý: Cho tam thức bậc hai
có biệt thức
.
-Nếu
thì tam thức
luôn cùng dấu với hệ số
với mọi giá trị của
. Tức là
.
– Nếu
thì tam thức
có nghiệm kép
và
luôn cùng dấu với hệ số
với mọi giá trị của
. Tức là:
hoặc
.
– Nếu
thì tam thức
có hai nghiệm phân biệt
. +Lúc này nếu
(trong khoảng 2 nghiệm) thì
luôn trái dấu với hệ số
; + nếu
thì
luôn cùng dấu với hệ số
.
Tức là: +
+
.
ÁP DỤNG
I. XÉT DẤU TAM THỨC
II. GIẢI BẤT PHƯƠNG TRÌNH BẬC HAI
III. GIẢI BÀI TOÁN CÓ THAM SỐ
(sẽ viết sau)
Chia sẻ:
- Thêm
-
Bình luận về bài viết này
-
Comments 75
Bình luận về bài viết này Hủy trả lời
-
Bài viết mới
- Viết pt mặt phẳng qua 3 điểm
- ĐỀ TUYỂN SINH VÀO LỚP 10 THPT THÀNH PHỐ HUẾ NĂM HỌC 2013-2014 (MÔN TOÁN) Xem tại đây.
- Đề kiểm tra học kỳ 1-Toán 12 (Thừa Thiên Huế) Năm học 2012-2013
- Đề tuyển sinh lớp 10 môn Toán năm 2012, Thừa Thiên Huế.
- Đề thi tuyển sinh lớp 10 chuyên Toán Quốc Học, Huế năm 2012
- Đề thi thử đại học số 8 năm 2012- (Tạp chí Toán học tuổi trẻ)
- Đề thi thử đại học số 6 năm 2012 (Toán học tuổi trẻ)
- Đề thi thử đại học môn Toán khối B năm 2012 – Chuyên Quốc học, Huế.
Xem bài theo Chuyên đề
Xem bài theo Chuyên đề Chọn chuyên mục ôn thi đại học (7) Giới thiệu (28) Học tập (3) phần mềm Toán (1) Thông báo KH kiểm tra (4) Tin tức (4) Toán lớp 10 (22) Hình học 10 (3) Đại số 10 (5) Toán lớp 11 (10) GIải tích 11 (4) Hình học KG 11 (1) Lượng giác (1) Toán lớp 12 (36) Giải tích (1) Hình học GT 12 (2) PT Mũ – Lôgarit (2) Số phức (3) Tích phân (4)Các trang chính
- About me
- Lời tâm sự
- Thi giải Toán trên Internet
- BDHSG
- Chuyên đề phương trình – hệ phương trình
- Geogebra
- Giải đáp
- Học Toán
- OTDH-P.H.E
- Cực trị hình học giải tích
- Giải đề thi thử đại học môn Toán 2010
- Khảo sát hàm số
- Nguyên hàm-PP tính
- Tích phân-Ứng dụng
- Đề thi lần 1. Lớp PHE
- Đề thi thử Đại học 2009
- Giải đề số 08
- Giải đề số 09
- Giải đề số 10
- Giải đề số 11
- Giải đề só 12
- Giải đề số 13
- Giải đề số 14
- Giải đề số 16
- Lời giải đề 06
- Lời giải đề số 07
- Đường thẳng trong không gian
- Toán 10
- BĐT Côsi (Cơ bản)
- Các bài của học sinh
- Tam thức bậc hai
- Đề thi thử hk2, Toán 10
- Toán 11
- Giới hạn hàm số
- Ôn tập chương II (Đại số 11)
- Ôn tập học kỳ I (Toán 11)
- Toán 12
- Bài của học sinh
- Chuyên đề PT Mũ-Lôgarit
- Nguyên hàm
- Phương trình đường thẳng
- Tọa độ vectơ
- Đề cương ôn tập học kỳ 1-Toán 12
- Hướng dẫn giải- Đáp số (Ôn tập Toán 12, học kỳ 1)
- Đề cương ôn thi Tốt ghiệp
- Đánh công thức Toán trên Blog wordpress
- OTDH-P.H.E
- Soft
- Tài nguyên
- Toán Blog
- About me
Số lượt truy cập
- 1 955 549 lượt
Đang Online

Chào ngày mới

-
Rank
 Giáo dục-Khuyến học (Dân trí)
Giáo dục-Khuyến học (Dân trí)- Lỗi: có thể dòng không tin đang không hoạt động. Hãy thử lại sau.
- Tìm kiếm:
Được đánh giá cao nhất
Liên kết Web
Trường THPT Đặng Trần CônWeb học tập
- Ôn tập
- Ôn thi
- Blog Vật Lý THPT
- Diễn đàn dạy học Vật lý
- Diễn đàn hóa học phổ thông Hãy đăng ký làm thành viên để tham gia diễn đàn này
- Diễn đàn tóan học
- Học tiếng anh trực tuyến Trang web hỗ trợ bạn tự học tiếng Anh từ dex đến khó
- Học trực tuyến
- Học Vật lý trực tuyến Đăng ký để học và downnload bài tập tham khảo
- hocmai.vn
- Tìm hiểu hóa học Giới thiệu các nghiên cứu, các bài viết hay về hóa học
Ý kiến
hy trong Đề kiểm tra Hình học 10 (Tham… likemath trong Các bước khảo sát hàm số likemath trong Các bước khảo sát hàm số Lê Văn Hùng trong Giải đề số 2 (Đề thi thử đại h… ho thi thu trong Phương trình đường thẳng trong… dangloc trong Tính chẵn, lẻ của hàm số hatch slack trong Tính chẵn, lẻ của hàm số manhhanthtt trong Đề thi tuyển sinh lớp 10 chuyê… Khoa trong Đề thi tuyển sinh lớp 10 chuyê…
Blog tại WordPress.com.
Trang này sử dụng cookie. Tìm hiểu cách kiểm soát ở trong: Chính Sách Cookie- Theo dõi Đã theo dõi
-
 Đỗ Cao Long's Blog. Đã có 77 người theo dõi Theo dõi ngay
Đỗ Cao Long's Blog. Đã có 77 người theo dõi Theo dõi ngay - Đã có tài khoản WordPress.com? Đăng nhập.
-
-
-
 Đỗ Cao Long's Blog.
Đỗ Cao Long's Blog. - Theo dõi Đã theo dõi
- Đăng ký
- Đăng nhập
- URL rút gọn
- Báo cáo nội dung
- Xem toàn bộ bài viết
- Quản lý theo dõi
- Ẩn menu
-
Từ khóa » Khi Tam Thức Có Nghiệm Kép Thì
-
Lý Thuyết Dấu Của Tam Thức Bậc Hai | SGK Toán Lớp 10
-
Lý Thuyết Dấu Của Tam Thức Bậc Hai Và Các Bài Tập Vận Dụng
-
Tam Thức Bậc 2 Là Gì ? Xét Dấu Tam Thức Bậc 2 Toán Lớp 8, Lớp 9 ...
-
Phương Trình Có Nghiệm Kép Khi Nào
-
Cách Xét Dấu Của Tam Thức Bậc 2 Và Bài Tập áp Dụng
-
Tổng Hợp Dạng Toán Về Phương Trình Bậc 2 Một ẩn Thông Dụng Nhất.
-
Bài Tập Về Xét Dấu Của Tam Thức Bậc 2, Bất Phương Trình Bậc 2 Và Lời ...
-
Dấu Của Tam Thức Bậc Hai - Lý Thuyết Và Dạng Toán Liên Quan - VOH
-
Hướng Dẫn 4 Cách Xét Dấu Của Tam Thức Bậc Hai (có Ví Dụ)
-
Lý Thuyết, Dấu Của Tam Thức Bậc Hai. - Boxthuthuat
-
Dấu Của Tam Thức Bậc Hai - Toán Học Lớp 10 - Baitap123
-
[PDF] DẤU CỦA TAM THỨC BẬC HAI: F(x) = Ax2 + Bx + C (a≠0)
-
Xét Dấu Bất Phương Trình Bậc 2 Và Bài Tập Áp ...
-
Cách Giải Nhanh Bất Phương Trình Bậc 2
Toi muon tham gia dien dan de hoc hoi doi chut duoc ko ah.
ThíchThích
Trả lờiem chao thầy.thầy ah em là học sinh tốt nghiệp khoá trước vì thế chương trình cải cách em không rõ lắm.thầy có thể giúp em phần tam thức bậc hai không?phần định lí đảo không được dùng nữa thì khi câu hỏi co phần đó thì làm thế nào ah.thầy có thể hồi âm sớm giúp em được không ạhem cám ơn thầy nhiêu
ThíchThích
Trả lờiEm có thể đọc thêm bài viết mà mình đã dùng một cách khác để xử lý bài toán đó nhé (Xem) ! Ngoài ra có thể dùng PP hàm số để giải quyết .
ThíchThích
Trả lờisao chi co phan bia ma khong co noi dung vay
ThíchThích
Trả lờitoi muon xem lai phan xet dau tam thuc bac hai. giup toi voi.cam on rat nhieu!
ThíchThích
Trả lờisao ban ko viet lot cac phan con lai
ThíchThích
Trả lờisao ban ko viet lot cac phan con lai hjhjhjhj:))
ThíchThích
Trả lờithay` oi sao ma truong trinh` cai? cach kho’ wa’ vay. troi` bo’ ai ma` hok noi? bao nhiu cai’ cong thuc +……… dc thay` co’ cach nao` chi? em cai’
ThíchThích
Trả lờithay` oi sao ma truong trinh` cai? cach kho’ wa’ vay. troi` bo’ ai ma` hok noi? bao nhiu cai’ cong thuc +……… thay` co’ cach nao` chi? em cai’
ThíchThích
Trả lờicac ban chiu kho mua sach moi ve ma doc chu online thje nj chj co noj dung tom tat thuj.
ThíchThích
Trả lờidoi voi tam thuc bac ba thi sao ak? lam sao de chung minh
ThíchThích
Trả lờicó cái gì mà mọi người than khó kinh dị vậy? thành ra học sinh bây giờ là siêu nhân à. đơn giản hóa đi sẽ thấy mấy cái kí hiệu toán học đó đơn giản và rất thú vị. hehe
ThíchThích
Trả lờiNhư thế thì có gi mà kinh dị
ThíchThích
Trả lờicảm ơn nhiều nha!!!!! yahoo: mucthu94
ThíchThích
Trả lờimong cac anh chi em giup minh xet dau tam thuc bac hai di
ThíchThích
Trả lờithầy có thể giúp em có cách hay nhất để nắm vững và làm bài tập dạng này linh hoạt đc ko ạ. em dôt lắm thầy ơi
ThíchThích
Trả lờisap kt 1t roy ma phan nay kho wak… thay giup em voi
ThíchThích
Trả lờiphan xet dau kho that. trong can hay gia tri tuyet doi thi phai giai sao? vi du 1 bai duoc khong?
ThíchThích
Trả lờiEm có bài nào cần hỏi hãy gửi đề lên blog rồi thầy trả lời cho.
ThíchThích
Trả lờicho hàm số x^2 + 3x + m =0 tìm m để PT có hai nghiệm và 2 nghiệm này nhỏ hơn hai nghiệm của PT x^2 – 3x + m + 2=0 Thầy ơi giúp em với
ThíchThích
Trả lờithầy ơi sao lâu thế. em đợi t nãy đến giờ, t có thể trả lời nhanh cho em tí được không ạ
ThíchThích
Trả lờiEm thông cảm. Thầy chỉ online được vào buổi tối. Ngày còn phải soạn bài và đi dạy nữa em à.
ThíchThích
Trả lờiVâng ! em cám ơn Thầy nhiều. Hẹn gặp lại Thầy nữa nha.
ThíchThích
Trả lờiĐiều kiện để phương trình có hai nghiệm (phân biệt) là:
có hai nghiệm (phân biệt) là:  . Điều kiện để phương trình
. Điều kiện để phương trình  có hai nghiệm (phân biệt) là:
có hai nghiệm (phân biệt) là:  . Giả sử
. Giả sử 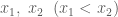 là hai nghiệm của
là hai nghiệm của  và
và  là hai nghiệm của
là hai nghiệm của  Lúc đó nghiệm lớn nhất của
Lúc đó nghiệm lớn nhất của  là :
là :  và nghiệm nhỏ nhất của
và nghiệm nhỏ nhất của  là:
là:  . Điều kiện cần và đủ để hai nghiệm của
. Điều kiện cần và đủ để hai nghiệm của  nhỏ hơn hai nghiệm của
nhỏ hơn hai nghiệm của  là
là 

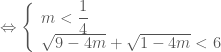

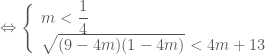

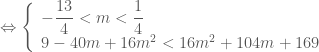


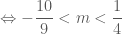 Kết luận: Giá trị cần tìm của
Kết luận: Giá trị cần tìm của  thỏa yêu cầu bài toán là
thỏa yêu cầu bài toán là  ——–
——–
ThíchThích
Trả lờiThầy ơi giúp em giải giùm bài toán này với nhé ! Đề: cho ba số thực dương a,b,c thỏa mãn abc=1 Chứng minh rằng 1/(a+b+1)+1 /(b+c+1)+1/(c+a+1)≤1
ThíchThích
Trả lờiThầy ơi em đang đợi thầy đấy. Mai phải trả bài cho cô giáo rồi thầy ơi
ThíchThích
Trả lờiThầy không mạnh về bất đẳng thức lắm. Trong lúc chờ đợi em thử hỏi trên diễn đàn khác đã em nhé ! — Khi nào có hướng giải bài tập này, em viết lên blog này để thầy tham khảo nhé ! —– Thầy có hướng giải như sau: Đặt . Ta có
. Ta có 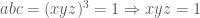 (vì
(vì  ) Để ý rằng (một kết quả ở bài tập SGK Toán 10):
) Để ý rằng (một kết quả ở bài tập SGK Toán 10): 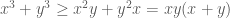 Tương tự:
Tương tự: 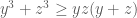 ;
; 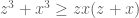 . Suy ra:
. Suy ra:  . hay
. hay  Tương tự, ta có:
Tương tự, ta có: 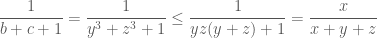 .
.  . Cộng 3 bất đẳng thức cuối theo vế ta được:
. Cộng 3 bất đẳng thức cuối theo vế ta được: 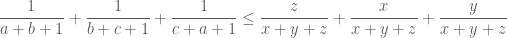
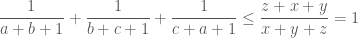
ThíchThích
Trả lờiem cam on thay nhieu. nhung bai toan dang nay em hoc ngo lam thay oi
ThíchThích
Trả lờiUhm. Chuyên đề này khó mà em.
ThíchThích
Trả lờiThầy ơi giúp em các bài toán này với nha Đề bài: Chứng minh rằng:Nếu hai phương trình: f¬¬1(x) = x2 + b1x + c =0 và f2(x) = x2 +b2x + c2 = 0 vô nghiệm là phương trình f1(x) + f2(x) = 0 cũng vô nghiệm.
ThíchThích
Trả lờiEm đánh đề lại cho rõ ràng nhé. Số mũ của lũy thừa phải rõ ràng. Ở trên c2 và b1 , b2 là gì vậy ? hay
hay  ?
?  là
là 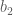 hay
hay  ?
?
ThíchThích
Trả lờiCho phương trình: f(x) = (m+2)x2 – 2(m-1)x+m-2=0 (m là tham số) a) Giải bất phương trình f(x) 0 theo tham số m c) Tìm m để phương trình f(x) = 2 có 2 nghiệm thuộc [-1;1]
ThíchThích
Trả lờiPhương trình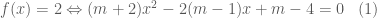 ———————- Câu b: Trường hợp 1:
———————- Câu b: Trường hợp 1:  ta có
ta có  trở thành:
trở thành:  Như vậy trường hợp này
Như vậy trường hợp này  chỉ có một nghiệm duy nhất
chỉ có một nghiệm duy nhất 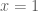 . Trường hợp 2:
. Trường hợp 2:  Khi đó
Khi đó  là phương trình bậc hai và có hai nghiệm
là phương trình bậc hai và có hai nghiệm 

 Hai nghiệm của
Hai nghiệm của  trong trường hợp này là:
trong trường hợp này là:  ;
; 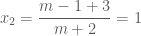 Nhận thấy nghiệm
Nhận thấy nghiệm ![x_2 = 1 \in [-1;1]](https://s0.wp.com/latex.php?latex=x_2+%3D+1+%5Cin+%5B-1%3B1%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) DO đó, phương trình
DO đó, phương trình  có hai nghiệm thuộc đoạn
có hai nghiệm thuộc đoạn ![[-1;1]](https://s0.wp.com/latex.php?latex=%5B-1%3B1%5D+&bg=ffffff&fg=4e4e4e&s=0&c=20201002) khi và chỉ khi
khi và chỉ khi 


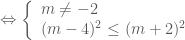
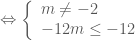
 Kết luận: Với mọi
Kết luận: Với mọi  thì yêu cầu bài toán được thỏa mãn.
thì yêu cầu bài toán được thỏa mãn.
ThíchThích
Trả lờivâng em cám ơn thầy nhiều em đánh lại thầy giúp em với nha
ThíchThích
Trả lờiBài 1: Chứng minh rằng nếu hai phương trình: f1(x) = x2+b1x+c1 =0 Và f2(x)= x2+b2x+c2 =0 vô nghiệm thì phương trình f1(x)+f2(x) =0 cũng vô nghiệm. thầy ơi b1 b2 c1 c2 là số ở dưới không phải số mũ, Bài 2: Cho b và c là hai số khác 0: thỏa mãn 1/b+1/c=1/2 Chứng minh rằng ít nhất một trong hai phương trình sau phải có nghiệm: x2+ bx+c=0 (1) và x2+cx+b=0 (2). Bài 3: Cho phương trình:f(x)=ax2+bx+c=0 (a khác 0) Chứng minh rằng: nếu phương trình f(x)=x vô nghiệm thì phương trình f[f(x)]=x cũng vô nghiệm.
Cám ơn thầy nhiều, thầy giúp em với
ThíchThích
Trả lờiPhương trình vô nghiệm nên ta có
vô nghiệm nên ta có 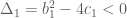 Phương trình
Phương trình 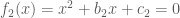 vô nghiệm nên ta có
vô nghiệm nên ta có 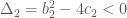 Phương trình
Phương trình 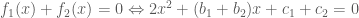 có
có  Ta phải chứng mính
Ta phải chứng mính 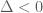 Thật vậy, ta có:
Thật vậy, ta có:  Chú ý rằng:
Chú ý rằng:  Suy ra:
Suy ra: 

 Ta có điều phải chứng minh.
Ta có điều phải chứng minh.
ThíchThích
Trả lờiBài 2: Cho b và c là hai số khác 0 thỏa mãn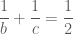 Chứng minh rằng ít nhất một trong hai phương trình sau phải có nghiệm:
Chứng minh rằng ít nhất một trong hai phương trình sau phải có nghiệm:  và
và  . ——————— Để
. ——————— Để  hoặc
hoặc  có nghiệm ta cần chứng minh biệt thức delta của một trong hai phương trình đó không âm. Phương trình
có nghiệm ta cần chứng minh biệt thức delta của một trong hai phương trình đó không âm. Phương trình  có
có 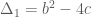 . Phương trình
. Phương trình 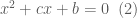 có
có 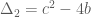 Ta cần chứng minh
Ta cần chứng minh 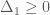 hoặc
hoặc 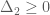 . Ta sẽ chứng minh bằng phản chứng. Giả sử cả hai phương trình
. Ta sẽ chứng minh bằng phản chứng. Giả sử cả hai phương trình  đều vô nghiệm, tức là
đều vô nghiệm, tức là 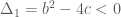 và
và 
 Từ giả thiết ta có
Từ giả thiết ta có  (vì
(vì 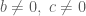 ) Suy ra :
) Suy ra :  Như vậy,
Như vậy, 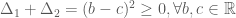 Điều này chứng tỏ
Điều này chứng tỏ  không thể xảy ra đồng nghĩa với giả thiết đưa ra là không thể xảy ra. Từ đó suy ra một trong hai phương trình đã cho phải có nghiệm.
không thể xảy ra đồng nghĩa với giả thiết đưa ra là không thể xảy ra. Từ đó suy ra một trong hai phương trình đã cho phải có nghiệm.
ThíchThích
Trả lờiBài 3: Cho phương trình: (a khác 0) Chứng minh rằng: nếu phương trình
(a khác 0) Chứng minh rằng: nếu phương trình 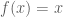 vô nghiệm thì phương trình
vô nghiệm thì phương trình ![f[f(x)]=x](https://s0.wp.com/latex.php?latex=f%5Bf%28x%29%5D%3Dx&bg=ffffff&fg=4e4e4e&s=0&c=20201002) cũng vô nghiệm. —————– Với bài này thầy có hướng giải theo phương pháp chiều biến thiên của hàm số như sau: Xét hàm số
cũng vô nghiệm. —————– Với bài này thầy có hướng giải theo phương pháp chiều biến thiên của hàm số như sau: Xét hàm số 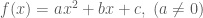 . Xét trường hợp
. Xét trường hợp  khi đó hàm số đồng biến trên khoảng
khi đó hàm số đồng biến trên khoảng  và nghịch biến trên khoảng
và nghịch biến trên khoảng 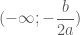 Phương trình
Phương trình 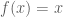 vô nghiệm nên ta có
vô nghiệm nên ta có 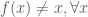 . Không mất tổng quát, giả sử
. Không mất tổng quát, giả sử  . TH1: Trên khoảng
. TH1: Trên khoảng  ta có
ta có  và hàm số đồng biến suy ra
và hàm số đồng biến suy ra  . Từ
. Từ 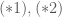 suy ra
suy ra  , tức là phương trình
, tức là phương trình ![f[f(x)]=x](https://s0.wp.com/latex.php?latex=f%5Bf%28x%29%5D%3Dx&bg=ffffff&fg=4e4e4e&s=0&c=20201002) vô nghiệm. TH2: Trên khoảng
vô nghiệm. TH2: Trên khoảng 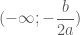 ta có $latex
ta có $latex 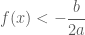 vì $latex
vì $latex  là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm số 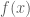 . Suy ra:
. Suy ra: ![f[f(x)] > f(-\dfrac{b}{2a}) \; \; (*3)](https://s0.wp.com/latex.php?latex=f%5Bf%28x%29%5D+%3E+f%28-%5Cdfrac%7Bb%7D%7B2a%7D%29+%5C%3B+%5C%3B+%28%2A3%29&bg=ffffff&fg=4e4e4e&s=0&c=20201002) (vì hàm số
(vì hàm số 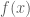 đồng biến trên khoảng
đồng biến trên khoảng  ) mà
) mà  (ta đang xét trên khoảng
(ta đang xét trên khoảng 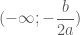 và
và  (theo
(theo 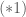 Do đó từ
Do đó từ 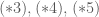 ta có
ta có ![f[f(x)] > f(-\dfrac{b}{2a}) > -\dfrac{b}{2a} > x](https://s0.wp.com/latex.php?latex=f%5Bf%28x%29%5D+%3E+f%28-%5Cdfrac%7Bb%7D%7B2a%7D%29+%3E+-%5Cdfrac%7Bb%7D%7B2a%7D+%3E+x+&bg=ffffff&fg=4e4e4e&s=0&c=20201002) . Điều này chứng tỏ phương trình
. Điều này chứng tỏ phương trình ![f[f(x)]=x](https://s0.wp.com/latex.php?latex=f%5Bf%28x%29%5D%3Dx&bg=ffffff&fg=4e4e4e&s=0&c=20201002) cũng vô nghiệm. Trường hợp
cũng vô nghiệm. Trường hợp  làm tương tự. Kết luận: Nếu phương trình
làm tương tự. Kết luận: Nếu phương trình 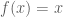 vô nghiệm thì phương trình
vô nghiệm thì phương trình ![f[f(x)]=x](https://s0.wp.com/latex.php?latex=f%5Bf%28x%29%5D%3Dx&bg=ffffff&fg=4e4e4e&s=0&c=20201002) cũng vô nghiệm.
cũng vô nghiệm.
ThíchThích
Trả lờiCho thầy hỏi điều này nhé. Có phải em đang học chương trình nâng cao hay chuyên toán không vậy ? Những bài em hỏi rất khó với học sinh chương trình cơ bản.
ThíchThích
Trả lờiem cám ơn thầy. Em học ở lớp chọn của trường nên những bài thầy giáo ra nó khó với em quá, em bảo thầy dạy dễ một chút nhưng không được, nếu không học được thì phải chuyển lớp, điều đó em không muốn. Thầy đồng hành cùng với em nha, giờ em chỉ biết tham khảo nơi thầy là dễ thôi. chúc thầy luôn bình an và hanh phúc.
ThíchThích
Trả lờiVâng. Mong rằng có thể giúp được các em học tập tốt hơn.
ThíchThích
Trả lờichào thầy ạ em có bài toán này mong thầy giúp em với ạ cho f(x)=a.x^2+b.x+c biết 13a+b+2c=0 chứng tỏ f(-2).f(-3)<=0 cảm ơn thầy ạ
ThíchThích
Trả lờiNhận xét: Bài toán này không chính xác. Chẳng hạn, xét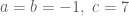 thỏa mãn
thỏa mãn 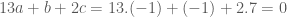 Ta có
Ta có  và
và 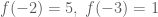 , khi đó
, khi đó  —————— Em xem lại đề bài nhé !
—————— Em xem lại đề bài nhé !
ThíchThích
Trả lờiem chao thay. Thay giup em giai bai toan nay voi: Cho đường thẳng (m – 1)x + 2y – 4m + 1 = 0 Tìm m để đường thẳng cắt Hypecbol tại hai điểm phân biệt thuộc cùng một nhánh của Hypec (H)
ThíchThích
Trả lờiEm chưa viết phương trình của Hyperbol (H). EM gủi lên rồi thầy hướng dẫn nhé !
ThíchThích
Trả lờivâng em cám ơn thầy em viết rồi thầy hướng dẫn em với.
ThíchThích
Trả lờiThầy ơi phương trình Hypebol x2/9 – y2/4 = 1
ThíchThích
Trả lờiPhương trình hoành độ giao điểm của đường thẳng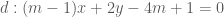 và hyperbol
và hyperbol  :
: 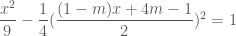
 Phương trình
Phương trình  có
có 
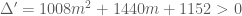 với mọi
với mọi  . DO đó
. DO đó  luôn có hai nghiệm phân biệt với mọi
luôn có hai nghiệm phân biệt với mọi  . Nhận xét: Hai nhánh của
. Nhận xét: Hai nhánh của 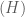 nằm hai phía của trục tung, do đó điều kiện để
nằm hai phía của trục tung, do đó điều kiện để  cắt
cắt 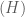 tại hai nhánh của
tại hai nhánh của 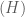 là phương trình
là phương trình  có hai nghiệm trái dấu
có hai nghiệm trái dấu 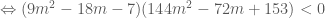

ThíchThích
Trả lờiem am on Thay nhieu. Thay giai ho em bai nay voi nha. (2x+1)/(x2∓5x+6)+3x/(x2+10x+1) ≥3
ThíchThích
Trả lờiCó phải đề yêu cầu chứng minh: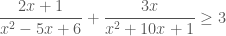 Em kiểm tra lại xem. Nếu đề như vậy thì có vấn đề !
Em kiểm tra lại xem. Nếu đề như vậy thì có vấn đề !
ThíchThích
Trả lờivang dang toan nhu vay thay a dang do thi lam the nao ha thay, thay huong dan em voi
ThíchThích
Trả lờiĐề em hỏi lần trước không đúng. Em xem và viết lại rồi thầy hướng dẫn thêm.
ThíchThích
Trả lờivang dang nhu vay thay a Thay cho em vi du ve dang do va huong dan cho em voi
ThíchThích
Trả lờiThầy ơi giúp em bài toán này với Trong hệ trục tọa độ oxy cho hình chữ nhật tâm I (1/2. 0) phương trình AB là x – 2y + 2=0 và AB=2AD. Tìm tọa độ các đỉnh A,B,C,D. Biết đỉnh A có tọa độ âm
ThíchThích
Trả lờiGọi tọa độ của là
là  với
với  . DO
. DO  có tọa độ âm nên
có tọa độ âm nên  . Vì
. Vì 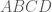 là hình chữ nhật nên
là hình chữ nhật nên 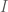 là trung điểm của các đoạn
là trung điểm của các đoạn 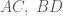 . Suy ra tọa độ các đỉnh
. Suy ra tọa độ các đỉnh 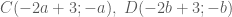 và
và  ,
, 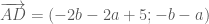 Theo giả thiết ta có
Theo giả thiết ta có 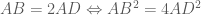
![\Leftrightarrow 4(b-a)^2+(b-a)^2=4[(-2b-2a+5)^2+(-b-a)^2]](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+4%28b-a%29%5E2%2B%28b-a%29%5E2%3D4%5B%28-2b-2a%2B5%29%5E2%2B%28-b-a%29%5E2%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![\Leftrightarrow 5(b-a)^2=4[(-2(b+a)+5)^2+(b+a)^2] \;\;\; (1)](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+5%28b-a%29%5E2%3D4%5B%28-2%28b%2Ba%29%2B5%29%5E2%2B%28b%2Ba%29%5E2%5D+%5C%3B%5C%3B%5C%3B+%281%29&bg=ffffff&fg=4e4e4e&s=0&c=20201002) Mặt khác
Mặt khác 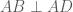 nên
nên 
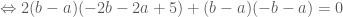
![\Leftrightarrow (b-a)[2(-2b-2a+5)-b-a]=0 \Leftrightarrow (b-a)[-5(a+b)+10]=0](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%28b-a%29%5B2%28-2b-2a%2B5%29-b-a%5D%3D0+%5CLeftrightarrow+%28b-a%29%5B-5%28a%2Bb%29%2B10%5D%3D0&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
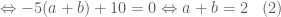 Thay vào
Thay vào  ta được
ta được ![5(b-a)^2=4[(-2.2+5)^2+2^2] \Leftrightarrow (b-a)^2=4](https://s0.wp.com/latex.php?latex=5%28b-a%29%5E2%3D4%5B%28-2.2%2B5%29%5E2%2B2%5E2%5D+%5CLeftrightarrow+%28b-a%29%5E2%3D4&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
 * Trường hợp 1:
* Trường hợp 1:  kết hợp với
kết hợp với  ta có hệ
ta có hệ  Giải hệ này được
Giải hệ này được 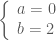 . Trường hợp này
. Trường hợp này  nên không thỏa mãn yêu cầu bài toán. * Trường hợp 2:
nên không thỏa mãn yêu cầu bài toán. * Trường hợp 2:  kết hợp với
kết hợp với  ta có hệ
ta có hệ 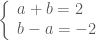 Giải hệ này được
Giải hệ này được 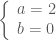 . Trường hợp này
. Trường hợp này 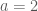 nên không thỏa mãn yêu cầu bài toán.
nên không thỏa mãn yêu cầu bài toán.
ThíchThích
Trả lờiEm kiểm tra lại yêu cầu bài toán xem sao nhé.
ThíchThích
Trả lờiem chào Thầy. Thầy giúp em bài toán này với nha Bài 1: Cho x, y khác 0, thay đổi thỏa mãn điều kiện (x+y).x.y = x2 + y2 – xy Tìm giá trị lớn nhất của biểu thức: P = 1/x3 + 1/y3
Bài 2: Trong hệ trục tọa độ oxy xác định đỉnh C của tam giác ABC biết hình chiếu vuông góc của C lên AB là H(-1; -1), đường phân giác trong của góc A có phương trình: x – y + 2 = 0 và đường cao kẻ từ B có phương trình 4x + 3y – 1 = 0.
ThíchThích
Trả lờiBài 1: Cho các số thực thỏa
thỏa  . Tìm giá trị lớn nhất của biểu thức
. Tìm giá trị lớn nhất của biểu thức  . ——— Ta có
. ——— Ta có  Từ giả thiết
Từ giả thiết  suy ra
suy ra  Đặt
Đặt  , từ giả thiết chia 2 vế cho
, từ giả thiết chia 2 vế cho 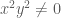 ta có:
ta có: 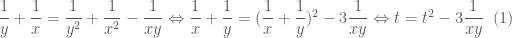 Theo bất đẳng thức
Theo bất đẳng thức  ta có
ta có  Kết hợp với
Kết hợp với  suy ra
suy ra 
 Vậy
Vậy 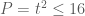
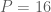 khi
khi 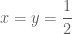 (khi
(khi  ). Suy ra giá trị lớn nhất của
). Suy ra giá trị lớn nhất của 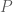 bằng
bằng  .
.
ThíchThích
Trả lờiBài 2: ——– Gọi là đường thẳng chứa cạnh
là đường thẳng chứa cạnh  khi đó
khi đó  đối xứng với đường thẳng chứa cạnh
đối xứng với đường thẳng chứa cạnh  qua đường phân giác trong góc
qua đường phân giác trong góc  là
là 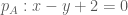 . Mà
. Mà  thuộc đường thẳng
thuộc đường thẳng  nên điểm
nên điểm 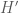 đối xứng của
đối xứng của  qua
qua 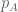 phải thuộc
phải thuộc  . Ta tìm được tọa độ
. Ta tìm được tọa độ  thuộc
thuộc  . (1) Mặt khác
. (1) Mặt khác  vuông góc với đường cao đi qua đỉnh
vuông góc với đường cao đi qua đỉnh 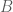 có phương trình
có phương trình 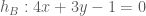 nên
nên  nhận
nhận  làm vecto pháp tuyến của
làm vecto pháp tuyến của  . (2) Từ (1) và (2) ta có phương trình của
. (2) Từ (1) và (2) ta có phương trình của  hay
hay 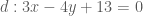 . Tọa độ của
. Tọa độ của  là nghiệm của hệ
là nghiệm của hệ  Giải hệ được
Giải hệ được  . Suy ra
. Suy ra  . Điểm
. Điểm 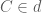 nên tọa độ có dạng
nên tọa độ có dạng  . Theo giả thiết
. Theo giả thiết  là hình chiếu của
là hình chiếu của  trên đường thẳng
trên đường thẳng  . Suy ra
. Suy ra 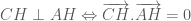 Giải ta tìm được
Giải ta tìm được 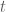 rồi suy ra tọa độ của
rồi suy ra tọa độ của  . Đáp số:
. Đáp số: 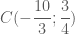 .
.
ThíchThích
Trả lờiEM CAM ON THAY
ThíchThích
Trả lờidạ chào thầy ak! thầy có thể giúp em một chút kiến thức ko ak?
ThíchThích
Trả lờithầy ơi giải giúp em bài toán này với. Bài1:cho M và N là 2 điểm trên 1 tiếp tuyến của (E) x^2/a^2 +x^2/b^2 =1 . sao cho mỗi điểm F1, F2 của E nhìn đoạn MN dưới góc vuông. Hãy xác định vị trí M, N trên tiếp tuyến ấy.
Bài 2. 1 đường kính bất kì của (E) : (E) x^2/a^2 +x^2/b^2 =1 . cắt (E) tại M và N. a. Chứng minh các tiếp tuyến của (E) tại M và N song song với nhau. b.Tìm mối liên hệ giữa a,b,c, m để (E) tiếp xúc với đường thẳng: y= kx+m
ThíchThích
Trả lờithầy ơi thầy bận à. sao lâu vậy
ThíchThích
Trả lờiThầy ơi thầy có thể cho em biết về phươg pháp so sánh 1 số với nghiệm cuả tam thức bậc 2 được không ạ?e khôg rõ vđề này lắm.mong thầy giúp em ạ!
ThíchThích
Trả lờiHiện nay trong chương trình chuẩn của toán phổ thông đã không đề cập về loại toán này và lý thuyết của nó nữa. Em muốn cần biết để nghiên cứu thêm thì cũng tốt.
ThíchThích
Trả lờithầy ơi giúp em bài này : 1/ cho hai phương trinh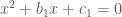 và
và  thỏa
thỏa  . Chứng minh rằng ít nhất một trong hai phương trình có nghiệm 2/ Từ hệ thức độc lập đối với m giữa các nghiệm là :
. Chứng minh rằng ít nhất một trong hai phương trình có nghiệm 2/ Từ hệ thức độc lập đối với m giữa các nghiệm là : 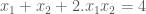 suy ra nghiệm kép của phương trình :
suy ra nghiệm kép của phương trình : .
.
ThíchThích
Trả lờiGiả sử cả hai phương trình đã cho đều vô nghiệm. Ta có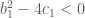 và
và  . Công hai bất đẳng thức theo vế, suy ra
. Công hai bất đẳng thức theo vế, suy ra 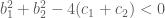 (*) Mặt khác
(*) Mặt khác 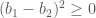
 (**) Theo tính chất bắc cầu, từ (*) và (**) suy ra:
(**) Theo tính chất bắc cầu, từ (*) và (**) suy ra: 
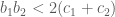 mâu thuẩn với giả thiết. Như vậy điều giả sử trên là không thể xảy ra. Do đó một trong hai phương trình đã cho có nghiệm.
mâu thuẩn với giả thiết. Như vậy điều giả sử trên là không thể xảy ra. Do đó một trong hai phương trình đã cho có nghiệm.
ThíchThích
Trả lờiCho em hoi: Tim dieu kien cua de Bat PT sau co nghiem
de Bat PT sau co nghiem  . Huong dan gium em nhanh voi. Ngay mai em thi roi
. Huong dan gium em nhanh voi. Ngay mai em thi roi
ThíchThích
Trả lờiDe thoi em ak, BPT vo nghiem khi a<0, delta =< 0. Tim dk cua m. Tu do neu len duoc dk de BPT co nghiem thoi.
ThíchThích
Trả lờiTrường hợp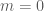 , bất phương trình trở thành
, bất phương trình trở thành  . Bất phương trình có tập nghiệm
. Bất phương trình có tập nghiệm  . (*1) Trường hợp
. (*1) Trường hợp  . Xét tam thức
. Xét tam thức 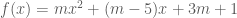 . Có
. Có 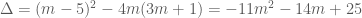 . Trường hợp
. Trường hợp 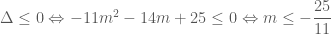 hoặc
hoặc  . Nếu
. Nếu  thì
thì  . (*2) Nếu
. (*2) Nếu 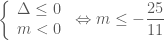 thì
thì  . (*3) Trường hợp
. (*3) Trường hợp  . Tam thức
. Tam thức 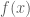 có hai nghiệm phân biệt
có hai nghiệm phân biệt 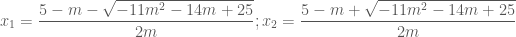 . và
. và  hoặc
hoặc  ,
, 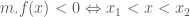 (*4). Dễ nhận thấy, trong các trường hợp (*1), (*2), (*4) thì bất phương trình đã cho có nghiệm. Vậy, giá trị của
(*4). Dễ nhận thấy, trong các trường hợp (*1), (*2), (*4) thì bất phương trình đã cho có nghiệm. Vậy, giá trị của  cần tìm là:
cần tìm là:  .
.
ThíchThích
Trả lờiPhai ko thay?
ThíchThích
Trả lờiXem lời giải chi tiết ở đây.
ThíchThích
Trả lờiThầy ơi giúp e về bt dấu của tam thức bậc 2 : x2-3×2+2 =0
ThíchThích
Trả lờiX2-3×2+3 =0
ThíchThích
Trả lờiDấu tam thức bậc 2 x2-3×2+3=0
ThíchThích
Trả lời