Tập Hợp Con – Wikipedia Tiếng Việt

Bước tới nội dung

Nội dung

chuyển sang thanh bên ẩn

• Đầu
• 1 Định nghĩa
• 2 Ví dụ
• 3 Một số tính chất của quan hệ bao hàm
• 4 Tập các tập con của một tập hợp
• 5 Tham khảo

• Bài viết
• Thảo luận

Tiếng Việt

• Đọc
• Sửa đổi
• Sửa mã nguồn
• Xem lịch sử

Công cụ Công cụ chuyển sang thanh bên ẩn Tác vụ

• Đọc
• Sửa đổi
• Sửa mã nguồn
• Xem lịch sử

Chung

• Các liên kết đến đây
• Thay đổi liên quan
• Trang đặc biệt
• Liên kết thường trực
• Thông tin trang
• Trích dẫn trang này
• Lấy URL ngắn gọn
• Tải mã QR

In và xuất

• Tạo một quyển sách
• Tải dưới dạng PDF
• Bản để in ra

Tại dự án khác

• Wikimedia Commons
• Khoản mục Wikidata

Giao diện chuyển sang thanh bên ẩn Bách khoa toàn thư mở Wikipedia

Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. Mời bạn giúp hoàn thiện bài viết này bằng cách bổ sung chú thích tới các nguồn đáng tin cậy. Các nội dung không có nguồn có thể bị nghi ngờ và xóa bỏ.

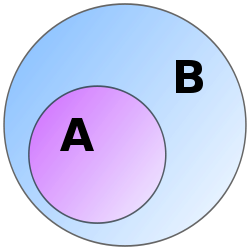
Trong Toán học, đặc biệt trong lý thuyết tập hợp, tập hợp A là một tập con (hay tập hợp con) của tập hợp B nếu A "được chứa" trong B. Quan hệ một tập là tập con của tập khác được gọi là quan hệ bao hàm.

Định nghĩa

[sửa | sửa mã nguồn]

Nếu A và B là các tập hợp và mọi phần tử của A cũng là phần tử của B, thì:

A là tập con của B (hay A chứa trong B), ký hiệu A ⊆ B {\displaystyle A\subseteq B} , hay tương đương (B là tập chứa của A (hay B chứa A), ký hiệu B ⊇ A . {\displaystyle B\supseteq A.}

Nếu A là tập con của B, nhưng có ít nhất 1 phần tử của B không là phần tử của A thì A được gọi là tập hợp con thực sự (hay tập con đích thực) của B, ký hiệu A ⊊ B . {\displaystyle A\subsetneq B.}

hay tương đương

• B là tập cha thực sự của A, ký hiệu B ⊋ A . {\displaystyle B\supsetneq A.}

Một số tài liệu cũng dùng ký hiệu A ⊂ B {\displaystyle A\subset B} thay cho A ⊆ B {\displaystyle A\subseteq B} , và B ⊃ A {\displaystyle B\supset A} thay cho B ⊇ A {\displaystyle B\supseteq A} với ý nghĩa tương tự. Tuy nhiên, nếu chi li ra thì ký hiệu A ⊆ B {\displaystyle A\subseteq B} được hiểu rằng A là tập con của B hoặc có thể bằng B, còn ký hiệu A ⊂ B {\displaystyle A\subset B} ít mang ý nghĩa A có thể bằng B hơn.

Tương tự như vậy trong số học, khi viết x ≤ y {\displaystyle x\leq \;y} thì x có thể nhỏ hơn y, có thể bằng y, nhưng nếu viết x < y {\displaystyle x<\;y} thì có nghĩa là x chỉ nhỏ hơn y chứ không thể bằng y.

Ví dụ

[sửa | sửa mã nguồn]

• Tập {1, 2} là tập con thực sự của {1, 2, 3}.
• Một tập hợp là tập con của chính nó, nhưng không phải là tập con thực sự.
• Tập các số tự nhiên là tập con thực sự của tập các số hữu tỷ.
• Nếu d là một đường thẳng nằm trên mặt phẳng P thì d là tập con của P.
• ...

Một số tính chất của quan hệ bao hàm

[sửa | sửa mã nguồn]

• Quan hệ bao hàm là một quan hệ thứ tự, nó có các tính chất:
  • phản xạ: với mọi tập A có A ⊆ A {\displaystyle A\subseteq A} ,
  • phản đối xứng: ( A ⊆ B ) ( B ⊆ A ) ⇒ A = B {\displaystyle A\subseteq B)(B\subseteq A)\Rightarrow A=B} ;
  • và bắc cầu: ( A ⊆ B {\displaystyle A\subseteq B} )( B ⊆ C ) ⇒ A ⊆ C {\displaystyle B\subseteq C)\Rightarrow A\subseteq C} .
• Tuân theo luật hấp thụ với các phép hợp và giao các tập hợp: Nếu A ⊂ B {\displaystyle A\subset B} thì:
  • A ∩ B = A {\displaystyle A\cap B=A}
  • A ∪ B = B {\displaystyle A\cup B=B} .

Tập các tập con của một tập hợp

[sửa | sửa mã nguồn] Bài chi tiết: Tập lũy thừa

• Cho B là một tập hợp. Theo định nghĩa trên, tập rỗng (ký hiệu ∅) và chính tập B là tập con của nó. Như vậy mọi tập hợp khác rỗng có ít nhất hai tập con là rỗng và chính nó. Tập rỗng chỉ có một tập con là rỗng. Tập rỗng là tập con của mọi tập hợp.
• Nếu B là tập hữu hạn có n phần tử thì B có 2n tập con. Chẳng hạn nếu B = {a, b, c} thì B có 8 tập con là ∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}

Do đó người ta thường ký hiệu tập các tập con của tập hợp B là 2B.

• Nếu B là tập vô hạn, người ta chứng minh rằng các tập hợp B và 2B là không cùng lực lượng.
• Thông thường, trong một lĩnh vực nghiên cứu cụ thể, người ta thường xét các tập con của tập hợp tất cả các đối tượng cần nghiên cứu.

Tham khảo

[sửa | sửa mã nguồn]

• Jech, Thomas (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.

x t s Lý thuyết tập hợp
Tiên đề	Tiên đề cặp Tiên đề chính tắc Tiên đề chọn đếm được phụ thuộc toàn cục Tiên đề giới hạn kích thước Tiên đề hợp Tiên đề mở rộng Tiên đề nối Tiên đề tập lũy thừa Tiên đề tính dựng được Tiên đề vô hạn Tiên đề Martin Sơ đồ tiên đề thay thế tuyển lựa
Phép toán	Tích Descartes Phần bù Luật De Morgan Phép giao Tập lũy thừa Phép hợp Liên hiệp rời rạc Hiệu đối xứng
Khái niệm Phương pháp	Lực lượng Số đếm (lớn) Lớp (lý thuyết tập hợp) Vũ trụ kiến thiết Giả thiết continuum Lập luận đường chéo Phần tử (cặp được sắp, bộ) Họ Ép Song ánh Số thứ tự Quy nạp siêu hạn Sơ đồ Venn
Các dạng tập hợp	Đếm được Rỗng Hữu hạn (di truyền) Mờ Vô hạn vô hạn Dedekind Tính được Tập con ⋅ Tập chứa Đơn điểm Bắc cầu Không đếm được Tập hợp phổ dụng
Lý thuyết	Lý thuyết tập hợp thay thế Lý thuyết tập hợp tiên đề Lý thuyết tập hợp ngây thơ Định lý Cantor Zermelo Tổng quát Principia Mathematica New Foundations Zermelo–Fraenkel von Neumann–Bernays–Gödel Morse–Kelley Kripke–Platek Tarski–Grothendieck
Nghịch lý Vấn đề	Nghịch lý Russell Bài toán Suslin Nghịch lý Burali-Forti
Nhà lý thuyết tập hợp	Abraham Fraenkel Bertrand Russell Ernst Zermelo Georg Cantor John von Neumann Kurt Gödel Paul Bernays Paul Cohen Richard Dedekind Thomas Jech Thoralf Skolem Willard Quine
Thể loại

Lấy từ “https://vi.wikipedia.org/w/index.php?title=Tập_hợp_con&oldid=71895144” Thể loại:

• Lý thuyết tập hợp

Thể loại ẩn:

• Trang thiếu chú thích trong bài
• Trang sử dụng liên kết tự động ISBN