Tìm Cực Trị Của Hàm Số Y=x-sin2x 2 - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
 Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
- neymar
tìm cực trị của hàm số y=x-sin2x+2
Xem chi tiết Lớp 12 Toán Bài 2: Cực trị hàm số 3 0 Gửi Hủy
Gửi Hủy  Hương Trà 3 tháng 2 2016 lúc 18:34
Hương Trà 3 tháng 2 2016 lúc 18:34 
 Gửi Hủy
Gửi Hủy  Huỳnh Văn Thiện 31 tháng 5 2017 lúc 17:19
Huỳnh Văn Thiện 31 tháng 5 2017 lúc 17:19 TXĐ: R
y' = 1 - 2cos2x
y' = 0 ⇔x = kπ (k ∈ Z)
y'' = 2sin2x
x = kπ → y'' = 2 > 0
→ yCT = 1 tại x = kπ
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy  CÔNG CHÚA THẤT LẠC 2 tháng 6 2017 lúc 11:02
CÔNG CHÚA THẤT LẠC 2 tháng 6 2017 lúc 11:02 Mình thường làm cách đơn giản hơn như sau: 1) y = x – sin2x + 2 Vì hàm sin 2x tuần hoàn trên đoạn [-Pi , Pi] Nên ta chỉ cần xét y trên đoạn [ -Pi , Pi] Y ‘ = 1 – 2cos2x => y’ = 0 <> x = +or-Pi/6 + k2Pi = +or- Pi/6 thuộc [ - Pi, Pi ] Lập bảng biến thiên như bình thường hoặc tính y” như bạn hngth cũng được Thường thì người ta bò họ no k2Pi đi chỉ xét trên chu kì cua nó thôi. Cái này bạn có thể mở SGK 11( NC) chương LG sẽ thấy 2) Y = 3 – 2cosx + 1 – 2cos^2x = -2cos^2x – 2cosx + 4 Đặt: t = cosx , t thuộc [-1, 1] Y = f(t) = -2t^2 – 2t +4 , D= [-1, 1] Xét hàm f(t) như bình thường => hàm f(t) đạt CĐ tại t = -1/2 , fCĐ = f(-1/2) = 9/2 =>hàm y đạt CĐ tại x = +or-2P/3 + k2Pi và yCĐ = 9/2 Bài này mà giải theo cách trên giữ nguyên họ no thì giải tới sáng cũng chưa ra. Đây là 2 cách đơn giản nhất để tìm cực trị hs LG còn công thức thì ko có đâu
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sin2x – x
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  25 tháng 7 2018 lúc 2:00
25 tháng 7 2018 lúc 2:00 TXĐ: D = R
+ y' = 2cos2x – 1;
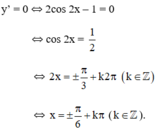
+ y" = -4.sin2x
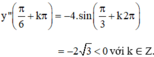
⇒ 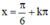 (k ∈ Z) là các điểm cực đại của hàm số.
(k ∈ Z) là các điểm cực đại của hàm số.
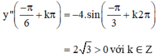
⇒ 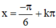 (k ∈ Z) là các điểm cực tiểu của hàm số.
(k ∈ Z) là các điểm cực tiểu của hàm số.
 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm cực trị của các hàm số sau:
a) y = sin2x
b) y = cosx − sinx
c) y = sin 2 x
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  17 tháng 4 2017 lúc 3:27
17 tháng 4 2017 lúc 3:27 a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔ 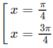
Bảng biến thiên:
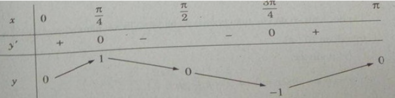
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
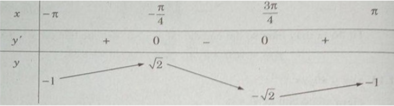
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
![]()
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
![]()
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
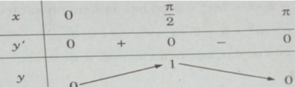
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm cực trị của các hàm số sau: y = sin2x
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  12 tháng 12 2017 lúc 4:22
12 tháng 12 2017 lúc 4:22 y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0; π ], ta có:
y' = 2cos2x
y' = 0 ⇔ 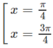
Bảng biến thiên:
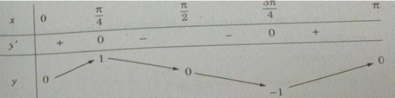
Do đó trên đoạn [0; π ] , hàm số đạt cực đại tại π /4 , đạt cực tiểu tại 3 π /4 và y CD = y( π /4) = 1; y CT = y(3 π /4) = −1
Vậy trên R ta có:
y CD = y( π /4 + k π ) = 1;
y CT = y(3 π /4 + k π ) = −1, k ∈ Z
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm cực trị của các hàm số sau: y = sin 2 x
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  23 tháng 4 2019 lúc 4:44
23 tháng 4 2019 lúc 4:44 Ta có:
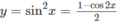
Do đó, hàm số đã cho tuần hoàn với chu kỳ π
Ta xét hàm số y trên đoạn [0; π ]:
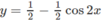
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = k π /2 (k ∈ Z)
Lập bảng biến thiên trên đoạn [0, π ]
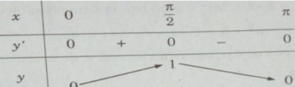
Từ đó, ta thấy hàm số đạt cực tiểu tại x = k π /2 với k chẵn, đạt cực đại tại x = k π /2 với k lẻ, và
y CT = y(2m π ) = 0; y CT = y(2m π ) = 0;
y CD = y((2m+1) π /2) = 1 (m ∈ Z)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Giá trị cực đại của hàm số y = x + sin2x trên 0 ; π là:
A. π 6 + 3 2
B. 2 π 3 + 3 2
C. 2 π 3 - 3 2
D. π 3 + 3 2
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  22 tháng 6 2017 lúc 14:03
22 tháng 6 2017 lúc 14:03 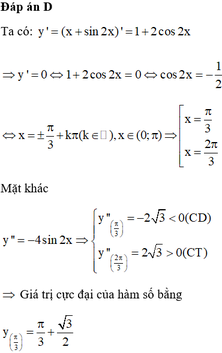
 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Giá trị cực đại của hàm số y = x + sin 2 x trên 0 ; π là:
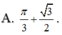
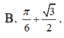
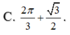
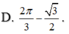
 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  15 tháng 11 2019 lúc 11:42
15 tháng 11 2019 lúc 11:42 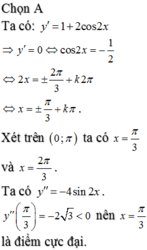
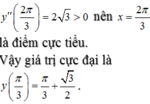
 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Tìm điểm cực đại của hàm số y = s i n 2 x + 3 c o s x + 1 với x ∈ (0; π)
A. x = 0
B. x = π
C. x = π 6
D. x = π 3
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  12 tháng 2 2019 lúc 7:54
12 tháng 2 2019 lúc 7:54 Ta có:
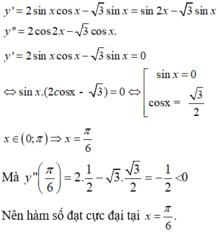
Chọn đáp án C.
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Biết rằng hàm số y = sin2x + b.cosx - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a - b
![]()
![]()
![]()
 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  16 tháng 6 2018 lúc 18:03
16 tháng 6 2018 lúc 18:03 Đáp án A
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Biết rằng hàm số y = sin 2 x + b cos 2 x - x ( 0 < x < π ) đạt cực trị tại các điểm x = π 6 và x = π 2 Tính giá trị của biểu thức T = a-b
A. 3 + 1 2
B. 3 - 1 2
C. 3 - 1
D. 3 + 1
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  20 tháng 5 2018 lúc 5:14
20 tháng 5 2018 lúc 5:14 Đáp án là B.
Ta có y , = 2 a . cos 2 x - 2 b sin 2 x - 1 .Để hàm số đạt cực trị các điểm x = π 2 và x = π 2 thì y , ( π 6 ) = 0 y , ( π 2 ) = 0 ⇔ a - 3 b - 1 = 0 - 2 a - 1 = 0 ⇔ a = - 1 2 b = - 3 2 ⇒ a - b = 3 - 1 2
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy Từ khóa » Tìm Cực Trị Của Hàm Số Y=x-sin2x+2
-
Tìm Cực Trị Của Hàm Số \(y=x-sin2x+2\) - Huong Duong
-
Tìm Cực Trị Hàm Số:y Bằng X-sin2x+2
-
Tìm Cực Trị Của Hàm Số \(y=x-sin2x+2\)
-
Tìm Cực Trị Của Hàm Số Y=x-sin2x+2 - Hoc24
-
Tài Liệu Về " Tìm Cực Trị Của Hàm Số Yx Sin2x 2 " 3 Kết Quả - 123doc
-
Tìm Cực Trị Của Hàm Số Y X Sin2x 2 - 123doc
-
Hàm Số Y = X – Sin 2x đạt Cực đại Tại Các điểm Nào Cho Dưới đây?...
-
Hàm Số Y = X – Sin 2x đạt Cực đại Tại Các điểm Nào Cho Dưới đây?
-
Tìm Cực Trị Của Hàm Số Y= Sin2x-x (dùng Cả Hai Quy Tắc ) Câu Hỏi ...
-
Tìm Cực Trị Của Hàm Số Y=sin2x-x | âm-nhạ
-
Giải Sách Bài Tập Toán 12 Bài 2: Cực Trị Của Hàm Số
-
Cho Hàm Số Y = X + Sin 2x + 2017.Tìm Tất Cả Các điểm Cực Tiểu Của