Tìm Cực Trị Của Hàm Trị Tuyệt đối, Xác định Số điểm Cực ... - HayHocHoi

Vậy cách tìm cực trị của hàm trị tuyệt đối như thế nào? Xác định số điểm cực trị của hàm trị tuyệt đối ra sao? chúng ta cùng tìm hiểu qua nội dung bài viết dưới đây.

I. Cách tìm cực trị của hàm trị tuyệt đối, xác định số điểm cực trị của hàm trị tuyệt đối

• Dạng 1: Hàm trị tuyệt đối dạng y = |f(x)|

- Ta có: 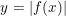 nên suy ra: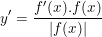 

- Số điểm cực trị của hàm số 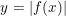 là số nghiệm bội lẻ của phương trình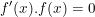 

→ Như vậy: Nếu gọi m là số điểm cực trị của hàm số y = f(x) và n là số giao điểm của đồ thị hàm số y = f(x) và trục hoành Ox thì m + n là số điểm cực trị của hàm số y = |f(x)| (chú ý bỏ đi các nghiệm bội chẵn (nghiệp kép)).

• Dạng 2: Hàm trị tuyệt đối dạng y = f(|x|)

- Ta có: 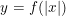 nên suy ra:  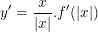từ đó ta có nhận xét sau:

- Hàm số đạt cực trị tại điểm x = 0.

- Số điểm cực trị dương của hàm số y = f(x) là m thì số điểm cực trị của hàm số y = f(|x|) là 2m + 1.

II. Bài tập minh họa cách tìm cực trị của hàm trị tuyệt đối, xác định số điểm cực trị của hàm trị tuyệt đối

* Bài tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:

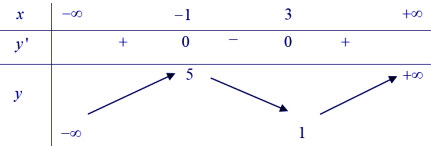
Đồ thị hàm số y = |f(x)| có bao nhiêu điểm cực trị?

* Lời giải:

Đây là bài toán dạng 1. Dựa vào bảng biến thiên ta thấy:

- Đồ thị hàm số y = f(x) cắt trục hoành y = 0 tại 1 điểm (đoạn đồ thị đi từ -∞ đến 5 sẽ cắt Ox) có 1 nghiệm) nên n = 1.

 Hiểu đơn giản là phương trình f(x) = 0 có 1 nghiệm đơn (bội lẻ).

- Hàm số y = f(x) có 2 điểm cực trị (y' = 0 có 2 nghiệm phân biệt) nên m = 2

⇒ Hàm số y = |f(x)| có 3 điểm cực trị.

* Bài tập 2: Cho hàm số y = f(x) có bảng biến thiên như sau:

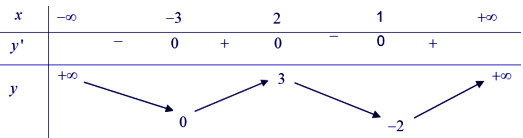
Đồ thị hàm số y = |f(x)| có bao nhiêu điểm cực trị?

* Lời giải:

Đây là bài toán dạng 1. Dựa vào bảng biến thiên ta thấy:

- Đồ thị hàm số y = f(x) cắt trục hoành Ox (y = 0) tại 2 điểm nên n = 2

(do có nghiệm kép (nghiệm bội chẵn) tại x = -3).

- Hàm số y = f(x) có 3 điểm cực trị (y' = 0 có 3 nghiệm phân biệt) nên m = 3.

⇒ Hàm số y = |f(x)| có 5 điểm cực trị.

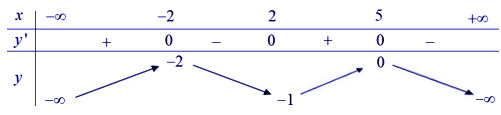
* Bài tập 3: Cho hàm số y = f(x) xác định trên R và có bảng biến thiên như sau:

* Lời giải:

Đây là bài toán dạng 2. Dựa vào bảng biến thiên ta thấy:

- Hàm số y = f(x) có 2 điểm cực trị có hoành độ dương là (2; -1) và (5; 0).

- Do đó hàm số y = f(|x|) có 2.2 + 1 = 5 điểm cực trị.

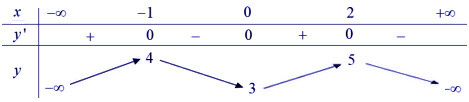
* Bài tập 4: Cho đồ thị hàm số y = f(x) có bảng biến thiên như sau:

* Lời giải:

Đây là bài toán dạng 2. Dựa vào bảng biến thiên ta thấy:

 (*)

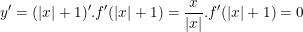
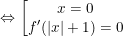Dựa vào đồ thị hàm số ta thấy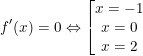 

Suy ra: 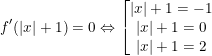 có 2 nghiệm

Do đó (*) chỉ có 3 nghiệm phân biệt, nên hàm số có 3 điểm cực trị.

* Bài tập 5: Tìm số điểm cực trị của hàm số: y = |(x - 1)(x - 2)2|

* Lời giải:

- Đặt f(x) = (x - 1)(x - 2)2

- Ta có: f'(x) = 3x2 - 10x + 8

 Cho f'(x) = 0 ⇔ 3x2 - 10x + 8 = 0

 ⇔ x = 2 hoặc x = 4/3

⇒ Hàm số f(x) có 2 điểm cực trị

- Mặt khác phương trình f(x) = (x - 1)(x - 2)2 = 0 có 1 nghiệm đơn x = 1

Ta có số điểm cực trị của hàm số y = |(x - 1)(x - 2)2| là tổng số điểm cực trị của hàm số f(x) = (x - 1)(x - 2)2 và số nghiệm đơn của f(x) = 0.

⇒ Vậy số điểm cực trị của hàm số y = |(x - 1)(x - 2)2| là 3.