Tìm Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số Y = 4x^2 + Căn 2x ...

Trang chủ » Gtnn Của 2x^2+3x-5 » Tìm Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số Y = 4x^2 + Căn 2x ...

Có thể bạn quan tâm

LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY XEM CHI TIẾT Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 4x^2 + căn 2x^2 + 3x + 2  + 6x + 2018 trên Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 4x^2 + căn 2x^2 + 3x + 2  + 6x + 2018 trên

Câu hỏi

Nhận biết

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 4{x^2} + \sqrt {2{x^2} + 3x + 2} + 6x + 2018\) trên đoạn \(\left[ {0;2} \right].\)

A. GTNN của hàm số bằng \(2018 + \sqrt 2 \)

GTLN của hàm số bằng \(2050\) B. GTNN của hàm số bằng \(2018\)

GTLN của hàm số bằng \(2020\) C. GTNN của hàm số bằng \(2018 + 2\sqrt 2 \)

GTLN của hàm số bằng \(2020\) D. GTNN của hàm số bằng \(2018 + 5\sqrt 2 \)

GTLN của hàm số bằng \(2050\)

Đáp án đúng: A

Lời giải của Tự Học 365

Giải chi tiết:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 4{x^2} + \sqrt {2{x^2} + 3x + 2}  + 6x + 2018\) trên đoạn \(\left[ {0;2} \right]\)

Ta có hàm số:

\(y = 4{x^2} + \sqrt {2{x^2} + 3x + 2}  + 6x + 2018 = 2\left( {2{x^2} + 3x + 2} \right) + \sqrt {2{x^2} + 3x + 2}  + 2014.\)

Đặt \(t = \sqrt {2{x^2} + 3x + 2} \;\;\;\left( {t \ge 0} \right) \Rightarrow {t^2} = 2{x^2} + 3x + 2.\)  

Khi đó ta có hàm số: \(y = f\left( t \right) = 2{t^2} + t + 2014.\)

Xét \(g\left( x \right) = 2{x^2} + 3x + 2\) với \(x \in \left[ {0;2} \right]\)

Ta có bảng:

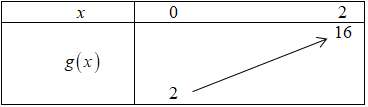
\( \Rightarrow \) Với \(x \in \left[ {0;2} \right]\) thì \(g\left( x \right) \in \left[ {2;16} \right]\)

\( \Rightarrow t = \sqrt {2{x^2} + 3x + 2}  = \sqrt {g\left( x \right)}  \in \left[ {\sqrt 2 ;4} \right]\)

Bài toán trở thành tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( t \right) = 2{t^2} + t + 2014\) trên đoạn \(\left[ {\sqrt 2 ;4} \right].\)

Ta có bảng:

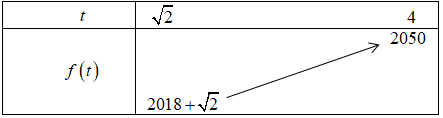
Vậy GTNN của hàm số bằng \(2018 + \sqrt 2 \) đạt được khi \(t = \sqrt 2 \) hay \(x = 0.\)

Vậy GTLN của hàm số bằng \(2050\) đạt được khi \(t = 4\) hay \(x = 2.\)

Chọn A.

Ý kiến của bạn Hủy

Δ

Luyện tập

Câu hỏi liên quan

  • TÌm a để 3 đường thẳng sau đây đồng qui: y=2x ; y= -x-3 ; y

    TÌm a để 3 đường thẳng sau đây đồng qui:

    y=2x ; y= -x-3 ; y= ax + 5

    Chi tiết
  • Định m sao cho : (m+1)x<sup>2</sup> – 2(m+1)x + 4 > 0 ; x ε

    Định m sao cho : (m+1)x2 – 2(m+1)x + 4 > 0 ; x ε R  (1)

    Chi tiết
  • Định m để f(x) = mx<sup>2</sup> – 2(m+1)x – m + 5 > 0 với x

    Định m để f(x) = mx2 – 2(m+1)x – m + 5 > 0 với x < 1

    Chi tiết
  • Giải Bất phương trình sau : 2x(3x-5) > 0

    Giải Bất phương trình sau :

    2x(3x-5) > 0

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx + m + 3 ≥ 0 với x ε R 

    Định m để  f(x) = mx2 – mx + m + 3 ≥ 0 với x ε R 

    Chi tiết
  • Khảo sát và vẽ đồ thị của hàm số :  1)y = 2|x| 2) y = 3√x

    Khảo sát và vẽ đồ thị của hàm số : 

    1)y = 2|x|

    2) y = 3√x

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx – 5 < 0 với x ε R   (1

    Định m để  f(x) = mx2 – mx – 5 < 0 với x ε R   (1)

    Chi tiết
  • Định m sao cho : x<sup>2</sup> – (3m – 2)x + 2m<sup>2</sup>

    Định m sao cho : x2 – (3m – 2)x + 2m2 – 5m – 2 > 0 ; x ε R

    Chi tiết
  • Định m để f(x) = x<sup>2</sup> – 2mx – m ≥ 0 với x > 0     

    Định m để f(x) = x2 – 2mx – m ≥ 0 với x > 0           

    Chi tiết
  • Định m sao cho : mx<sup>2</sup> – 10x – 5 ≤ 0 ; x ε R  (1)

    Định m sao cho : mx2 – 10x – 5 ≤ 0 ; x ε R  (1)

    Chi tiết

Đăng ký

Năm sinh 20012002200320042005200620072008200920102011201220132014201520162017201820192020 hoặc Đăng nhập nhanh bằng: đăng nhập bằng google (*) Khi bấm vào đăng ký tài khoản, bạn chắc chắn đã đoc và đồng ý với Chính sách bảo mật và Điều khoản dịch vụ của Tự Học 365.

Từ khóa » Gtnn Của 2x^2+3x-5