Tìm M để Bất Phương Trình Nghiệm đúng Với Mọi X
Có thể bạn quan tâm
Tìm tham số m để bất phương trình có nghiệm đúng với mọi x thuộc R
- A. Cách tìm m để bất phương trình nghiệm đúng với mọi x
- B. Tìm tham số m để bất phương trình nghiệm đúng với mọi x
- C. Bài tập tự rèn luyện tìm m để bất phương trình nghiệm đúng với mọi x
Bạn đang học chương trình Toán lớp 10 và gặp phải bài toán liên quan đến bất phương trình chứa tham số? Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách tìm m để bất phương trình nghiệm đúng với mọi x – một dạng bài quen thuộc nhưng cũng rất dễ gây nhầm lẫn nếu không nắm vững phương pháp. Đây là nội dung thuộc chuyên đề bất phương trình chứa tham số lớp 10, thường xuyên xuất hiện trong các đề kiểm tra và đề thi học kỳ. Hãy cùng khám phá cách giải nhanh, chính xác và tối ưu nhất để chinh phục dạng toán này nhé!
Tìm m để bất phương trình nghiệm đúng với mọi x thuộc R
Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại
A. Cách tìm m để bất phương trình nghiệm đúng với mọi x
Phương pháp: Đối với các bài toán tìm điều kiện để bất phương trình nghiệm đúng với mọi x hay bất phương trình vô nghiệm ta sử dụng các lập luận như sau: (ta xét với bất phương trình bậc hai một ẩn)
- f(x) > 0 vô nghiệm ⇔ f(x) ≤ 0 nghiệm đúng với ∀x ∈
 . Nghĩa là
. Nghĩa là 
- f(x) < 0 vô nghiệm ⇔ f(x) ≥ 0 nghiệm đúng với ∀x ∈
 . Nghĩa là
. Nghĩa là 
- f(x) ≥ 0 vô nghiệm ⇔ f(x) < 0 nghiệm đúng với ∀x ∈
 . Nghĩa là
. Nghĩa là 
- f(x) ≤ 0 vô nghiệm ⇔ f(x) > 0 nghiệm đúng với ∀x ∈
 . Nghĩa là
. Nghĩa là 
B. Tìm tham số m để bất phương trình nghiệm đúng với mọi x
Ví dụ 1: Cho bất phương trình (m - 1)x2 + 2mx - 3 > 0. Tìm giá trị của m để bất phương trình nghiệm đúng với mọi x thuộc tập số thực?
Hướng dẫn giải
Đặt (m - 1)x2 + 2mx - 3 = f(x)
TH1: m - 1 = 0 ⇒ m = 1. Thay m = 1 vào bất phương trình ta được: 2x - 3 > 0⇒ ![]() (Loại)
(Loại)
TH2: m - 1 ≠ 0 ⇔ m ≠ 1
Để bất phương trình f(x) > 0 nghiệm đúng với mọi x ![]()

Vậy không có giá trị nào của m để bất phương trình có nghiệm đúng với mọi x thuộc ![]() .
.
Ví dụ 2: Xác định tất cả các giá trị tham số m để các bất phương trình sau đúng với mọi x thuộc ![]() .
.
| a) (m - 3)x2 + (m + 1)x + 2 < 0 | b) (m - 1)x2 + (m - 3)x + 4 > 0 |
Hướng dẫn giải
a. Đặt (m - 3)x2 + (m + 1)x + 2 = f(x)
TH1: m - 3 = 0 ⇔ m = 3. Thay m = 3 vào bất phương trình ta được: 2x + 2 < 0 ⇔ x < -1 (Loại)
TH2: m - 3 ≠ 0 ⇔ m ≠ 3
Để bất phương trình f(x) < 0 nghiệm đúng với mọi x ![]()
![]()
Ta có: m2 - 6m + 25 = (m - 3)2 + 16 ≥ 16,∀m
Vậy không có giá trị nào của m để bất phương trình có nghiệm đúng với mọi x thuộc ![]()
b. Đặt (m - 1)x2 + (m - 3)x + 4 = f(x)
TH1: m - 1 = 0 ⇔ m = 1. Thay m = 1 vào bất phương trình ta được: -2x + 4 > 0 ⇔ x < 2 (Loại)
TH2: m - 1 ≠ 0 ⇔ m ≠ 1
Để bất phương trình f(x) > 0 nghiệm đúng với mọi x ![]()

![]()
Vậy ![]() thì bất phương trình có nghiệm đúng với mọi x thuộc
thì bất phương trình có nghiệm đúng với mọi x thuộc ![]() .
.
Ví dụ 3: Cho bất phương trình: ![]() . Tìm m để bất phương trình có nghiệm đúng với mọi x thuộc tập số thực?
. Tìm m để bất phương trình có nghiệm đúng với mọi x thuộc tập số thực?
Hướng dẫn giải
Ta có: ![]()
![]()
![]()
![]()
![]()
Nếu m = 1/2 thì (*) trở thành ![]()
Suy ra (*) không thỏa mãn với mọi x thuộc R
Nếu m khác 1/2 (*) đúng với mọi x thuộc R




![]()
Vậy ![]() thì bất phương trình có nghiệm đúng với mọi x thuộc tập số thực.
thì bất phương trình có nghiệm đúng với mọi x thuộc tập số thực.
Ví dụ 4: Số giá trị nguyên của tham số ![]() để bất phương trình
để bất phương trình ![]() nghiệm đúng ∀x ∈ [-5; 2] là:
nghiệm đúng ∀x ∈ [-5; 2] là:
A. Vô số B. 1 C. 3 D. 4
Hướng dẫn giải
Ta có:
![]()
![]()
Đặt ![]()
![]()
![]()
![]()
Vậy có duy nhất 1 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán, đó là giá trị ![]() .
.
Ví dụ 5: Tìm tất cả các giá trị của tham số m để bất phương trình ![]() nghiệm đúng
nghiệm đúng ![]() .
.
A. m ∈ R B. m ∈ (-2; 2)
C. m ∈ [-2; 2] D. m ∈ (-∞;-2] ∪ [2; +∞)
Hướng dẫn giải
Ta có ![]() có
có  nên
nên ![]() .
.
Do đó ![]() .
.
![]() Bất phương trình
Bất phương trình ![]() nghiệm đúng
nghiệm đúng ![]() nghiệm đúng
nghiệm đúng ![]() .
.
![]() .
.
C. Bài tập tự rèn luyện tìm m để bất phương trình nghiệm đúng với mọi x
Bài tập 1. Cho hàm số ![]() . Với giá trị nào của tham số m thì
. Với giá trị nào của tham số m thì ![]() .
.
A. m ≥ 1. B. m > 1. C. m > 0. D. m < 2.
Bài tập 2. Tam thức ![]() không âm với mọi giá trị của x khi
không âm với mọi giá trị của x khi
A. m < 3. B. m ≥ 3. C. m ≤ -3. D. m ≤ 3.
Bài tập 3. Có bao nhiêu giá trị nguyên của tham số m để với mọi ![]() biểu thức
biểu thức ![]() luôn nhận giá trị dương.
luôn nhận giá trị dương.
A. 27. B. 28. C. Vô số. D. 26.
Bài tập 4. Tìm các giá trị của m để biểu thức ![]()
A. m ∈ [2; 6] . B. m ∈ (-3; 9). C. ![]() . D. m ∈ (-9; 3).
. D. m ∈ (-9; 3).
Bài tập 5. Tìm tất cả các giá trị thực của tham số m để bất phương trình: ![]() có tập nghiệm
có tập nghiệm ![]() ?
?
A. m > -1 B. -1 ≤ m ≤ 3 C. -1 < m ≤ 3 D. -1 < m < -3
Bài tập 6. Tìm tất cả các giá trị của tham số m để tam thức bậc hai f(x) sau đây thỏa mãn ![]() ,
, ![]() .
.
A. m > 2019. B. m < 2019. C. m > 2017. D. m < 2017.
Bài tập 7. Tìm tham số m để ![]() luôn luôn âm
luôn luôn âm
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Bài tập 8. Tìm tất cả các giá trị của tham số m để bất phương trình![]() nghiệm đúng với mọi
nghiệm đúng với mọi ![]() .
.
A. m ∈ ∅. B. m ∈ (-2; 2).
C. m ∈ (-∞;-2] ∪ [2; +∞). D. m ∈ [-2; 2].
Bài tập 9. Tìm tất cả các giá trị của m để bất phương trình![]() nghiệm đúng với mọi
nghiệm đúng với mọi ![]()
A. ![]() . B.
. B. ![]() . C. -1 ≤ m ≤ 7 D. -1 < m < 7.
. C. -1 ≤ m ≤ 7 D. -1 < m < 7.
Bài tập 10. Tìm tập hợp các giá trị của tham số m để hàm số ![]() có tập xác định
có tập xác định ![]() .
.
A. [-1; 6]. B. (-1; 6). C. ![]() . D.
. D. ![]() .
.
Bài tập 11. Cho bất phương trình ![]() . Gọi S là tập hợp các số nguyên dương m để bất phương trình đúng với mọi
. Gọi S là tập hợp các số nguyên dương m để bất phương trình đúng với mọi ![]() . Khi đó số phần tử của
. Khi đó số phần tử của ![]() là
là
A. 2. B. 3. C. 1. D. 0.
Đáp án bài tập tự rèn luyện
Bài tập 1.
Chọn A
Ta có  .
.
Bài tập 2.
Chọn D
Yêu cầu bài toán ![]()
![]()

![]()
![]() .
.
Vậy ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Bài tập 11.
Chọn C
Cách 1:
Đặt ![]()
TH1: m - 2 = 0 ⇔ m = 2
![]() không thỏa đề
không thỏa đề
TH2: ![]()

Bảng xét dấu 

* Nếum > 6 thì ![]() không thỏa đề bài
không thỏa đề bài
* Nếu ![]() thì
thì ![]() thỏa đề bài
thỏa đề bài
* Nếu ![]() thì f(x) = 0 có hai nghiệm phân biệt
thì f(x) = 0 có hai nghiệm phân biệt ![]()
Bảng xét dấu f(x)
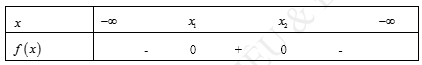
Khi đó ![]() không thỏa đề
không thỏa đề
* Nếu ![]() thì
thì ![]() có hai nghiệm phân biệt
có hai nghiệm phân biệt ![]()
Bảng xét dấu f(x)
Khi đó ![]()
![]()
![]()
![]()


So sánh điều kiện suy ra ![]() .
.
Vậy ![]() . Khi đó S = {1}.
. Khi đó S = {1}.
Cách 2:
Ta có ![]()
![]()
![]() .
.
Xét hàm số ![]() với
với ![]() .
.
Ta có 

Bảng biến thiên:
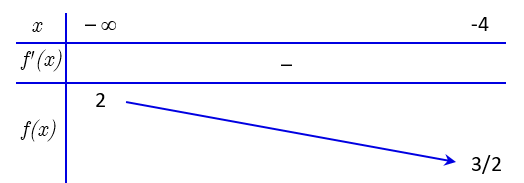
Bất phương trình ![]() nghiệm đúng với mọi x < -4
nghiệm đúng với mọi x < -4
![]() .
.
Vậy ![]() . Khi đó S = {1}.
. Khi đó S = {1}.
✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.
---------------------------------------------------------------
Trên đây là hướng dẫn chi tiết cách tìm m để bất phương trình nghiệm đúng với mọi x trong chương trình Toán lớp 10, thuộc chuyên đề bất phương trình chứa tham số. Hy vọng qua bài viết này, bạn đã nắm được phương pháp giải cụ thể, các bước lập luận logic cũng như những lưu ý quan trọng để tránh sai sót. Đừng quên luyện tập thêm nhiều bài tập tương tự để củng cố kỹ năng và tăng tốc độ giải nhanh hơn trong các kỳ thi. Nếu bạn thấy bài viết hữu ích, hãy chia sẻ cho bạn bè và theo dõi thêm nhiều chủ đề học tập thú vị khác tại website của chúng tôi!
Từ khóa » Có Nghiệm Với Mọi X Thuộc R
-
Nghiệm đúng Với Mọi X Thuộc R Là Gì - Toàn Thua
-
Tìm M để Bất Phương Trình Có Nghiệm đúng Với Mọi X Thuộc R?
-
Xác định M để Phương Trình Có Nghiệm Với Mọi X Thuộc R - Lazi
-
Tìm M để Bất Phương Trình Có Nghiệm đúng Với Mọi X - TopLoigiai
-
Toán 10 - Tìm M để BPT Có Nghiệm Với Mọi X Thuộc R - HOCMAI Forum
-
Tìm M để Bất Phương Trình Có Nghiệm Ôn Tập Toán 10
-
[ĐS 10] Tìm M để Bất Phương Trình Nghiệm đúng Với Mọi X Thuộc R
-
Tìm M Để Bất Phương Trình Có Nghiệm Đúng Với Mọi X Thuộc R ...
-
Bất Phương Trình ((x^2) - Mx - M >= 0 ) Có Nghiệm đúng Với Mọi
-
Tìm M để Các Bất Phương Trình (m – 3)2 + (m + 1)x + 2 < 0 đúng Với ...
-
Tìm Tất Cả Các Giá Trị Thực Của Tham Số M để Pt \( \left(m^2-1\right)\)x ...
-
Tìm M để Bất Phương Trình Sau Nghiệm đúng Với Mọi X Thuộc R
-
Tìm M Thuộc [0;2018] để Bất Phương Trình Có Nghiệm Với Mọi X Thuộc R