Tìm M để Hàm Số Có 5 Cực Trị

Có thể bạn quan tâm

Giải Toán - Hỏi đáp - Thảo luận - Giải bài tập Toán - Trắc nghiệm Toán online

Tất cả
- Bài tập Cuối tuần
- Toán 1
- Toán 2
- Toán 3
- Toán 4
- Toán 5
- Toán 6
- Toán 7
- Toán 8
- Toán 9
- Toán 10
- Toán 11
- Toán 12
- Test IQ
- Hỏi bài
- Đố vui Toán học
- Toán 1
- Toán 2
- Toán 3
- Toán 4
- Toán 5
- Toán 6
- Toán 7
- Toán 8
- Toán 9
- Toán 10
- Toán 11
- Toán 12

Giaitoan.com Toán 12 Chuyên đề Toán 12Tìm m để hàm số có 5 cực trị Cực trị của hàm sốNội dung

8 Đánh giá

Mua tài khoản GiaiToan Pro để trải nghiệm website GiaiToan.com KHÔNG quảng cáo & Tải tất cả các File chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Tìm m để hàm số có cực trị

Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, GiaiToan.com xin mời quý thầy cô và các bạn học sinh tham khảo tài liệu Tìm tham số m để hàm số có 5 cực trị. Bộ tài liệu giới thiệu đến bạn đọc cácphương pháp giải bài tập ứng dụng tìm tham số m để hàm số có cực trị cùng hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia. Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.

Tìm m để hàm số có 5 điểm cực trị

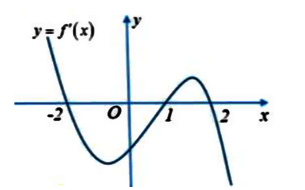
Ví dụ 1: Cho đồ thị hàm số y = f’(x) như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của m để hàm số y = f(|x| + m) có 5 điểm cực trị?

Tìm m để hàm số có 5 cực trị

A. 2	B. 3
C. 4	D. 8

Hướng dẫn giải

Hàm số y = f(|x| + m) là hàm số chẵn

Với x > 0, y = f(|x| + m) = f(x + m) có y’ = f’(x + m)

y’ = f’(x + m) = 0

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x + m = - 2} \\ {x + m = 1} \\ {x + m = 2} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - m - 2} \\ {x = - m + 1} \\ {x = - m + 2} \end{array}} \right.$

Hàm số y = f(|x| + m) có 5 điểm cực trị khi và chỉ khi y = f(|x| + m) có hai điểm cực trị dương hay:

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} { - m - 2 \leqslant 0} \\ { - m + 1 0} \end{array} \Leftrightarrow - 2 \leqslant m < 1} \right.$

Vậy có 3 giá trị nguyên của m để hàm số y = f(|x| + m) có 5 điểm cực trị.

Chọn đáp án B

Ví dụ 2: Có bao nhiêu giá trị nguyên của tham số m ∈ [-10; 10], để hàm số y = |mx3 – 3mx2 + (3m – 2)x + 2 – m| có 5 điểm cực trị?

A. 9	B. 11
C. 7	D. 10

Hướng dẫn giải

Xét các trường hợp như sau:

Trường hợp 1: Với m = 0

Thay vào hàm số y ta được y = |-2x + 2| có 1 điểm cực trị nên m = 0 loại

Trường hợp 2: Với m ≠ 0

Hàm số y = |mx3 – 3mx2 + (3m – 2)x + 2 – m| có 5 điểm cực trị khi và chỉ khi đồ thị hàm số f(x) = mx3 – 3mx2 + (3m – 2)x + 2 – m cắt trục hoành tại 3 điểm phân biệt

Xét phương trình

f(x) = 0

⇔ mx3 – 3mx2 + (3m – 2)x + 2 – m = 0

⇔ (x – 1)(mx2 – 2mx + m – 2) = 0

⇔ $\left[ {\begin{array}{*{20}{c}} {x = 1} \\ {m{x^2} - 2mx + m - 1 = 0\left( * \right)} \end{array}} \right.$

Để f(x) = 0 có 3 nghiệm phân biệt thì (*) có hai nghiệm phân biệt khác nghiệm x = 1

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m \ne 0} \\ {\Delta ' 0} \\ {m - 2m + m - 2 \ne 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m \ne 0} \\ {m 0} \\ { - 2 \ne 0} \end{array}} \right.$

Do m ∈ [-10; 10] => m ∈ (0; 10]

Vậy có 10 giá trị của m thỏa mãn

Chọn đáp án D

Ví dụ 3: Cho hàm số f(x) có đạo hàm f’(x) = (x + 1)2(x2 – 4x). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = f(2x2 – 12x + m) có đúng 5 điểm cực trị?

A. 17	B. 16
C. 18	D. 19

Hướng dẫn giải

Ta có:

g’(x) = (4x – 12).f’(2x2 – 12x + m)

= (4x – 12)(2x2 – 12x + m + 1)2(2x2 – 12x + m)(2x2 – 12x + m – 4)

Hàm số g(x) có đúng 5 điểm cực trị

=> g’(x) đổi dấu 5 lần

=> g’(x) = 0 có 5 nghiệm đơn phân biệt

=> Phương trình 2x2 – 12x + m = 0 có hai nghiệm phân biệt khác 3 và phương trình 2x2 – 12x + m – 4 = 0 có hai nghiệm phân biệt khác 3 và các nghiệm này khác nhau

Phương trình 2x2 – 12x + m = 0 có hai nghiệm phân biệt khác 3 và phương trình 2x2 – 12x + m – 4 = 0 có hai nghiệm phân biệt khác 3

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{\Delta _1}' 0} \\ {{\Delta _2}' 0} \\ {{{2.3}^2} - 12.3 + m \ne 0} \\ {{{2.3}^2} - 12.3 + m - 4 \ne 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {36 - 2m 0} \\ {36 - 2\left( {m - 4} \right) 0} \\ {m \ne 18} \\ {m \ne 22} \end{array}} \right. \Leftrightarrow m < 18$

Vậy với điều kiện m < 18 giả sử hai phương trình có nghiệm chung là a

Thay x = a vào hai phương trình đã cho ta được

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2{a^2} - 12a + m = 0} \\ {2{a^2} - 12a + m - 4 = 0} \end{array}} \right. \Rightarrow - 4 = 0\left( {loai} \right)$

Do đó các nghiệm của hai phương trình 2x2 – 12x + m = 0 và 2x2 – 12x + m – 4 = 0 luôn khác nhau.

Mà m là số nguyên dương nên m ∈ {1; 2; 3; ….; 17}

=> Có 17 giá trị của m thỏa mãn điều kiện đề bài

Chọn đáp án A

Ví dụ 4: Cho hàm số f(x) có f'(x) = (x2 - 16)(x + 1)(x2 - 4x + m - 4). Có bao nhiêu giá trị nguyên của tham số m thuộc [-2021; 2021] sao cho hàm số g(x) = f(x2) có 5 điểm cực trị?

A. 2025

B. 2026

C. 2021

D. 4043

Hướng dẫn giải

Ta có:

g'(x) = 2x.f'(x2) = 2x . (x4 - 16) . (x2 + 1) . (x4 - 4x2 + m - 4)

Ta có: g'(x) = 0

$\Rightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {{x^4} - 16 = 0} \\ {{x^4} - 4{x^2} + m - 4 = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 2} \\ {x = - 2} \\ {{x^4} - 4{x^2} + m - 4 = 0\left( * \right)} \end{array}} \right.$

Trường hợp 1: Phương trình (*) có nghiệm x = 0 => m - 4 = 0 => m = 4.

Thay m = 4 vào (*) ta có: x4 – 4x2 = 0 $\Rightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 2} \\ {x = - 2} \end{array}} \right.$

Khi đó g'(x) = 0 có 3 nghiệm bội chẵn nên hàm số g(x) không thể có 5 điểm cực trị nên m = 4 (Không thỏa mãn)

Trường hợp 2: Phương trình (*) có nghiệm x = 2 hoặc x = -2 => m - 4 = 0 => m = 4 (Không thảo mãn)

Trường hợp 3: Phương trình (*) có hai nghiệm đơn phân biệt khác 0 và khác 2 và khác -2 hay

t2 - 4t + m - 4 = 0 phải có hai nghiệm trái dấu (với t = x2) => m - 4 < 0 => m < 4

Khi đó g'(x) = 0 có 5 nghiệm phân biệt nên hàm số g(x) có 5 điểm cực trị

Kết hợp với điều kiện m thuộc [-2021; 2021] suy ra -2021 ≤ m < 4, (m là số nguyên) nên ta có 2025 giá trị nguyên của tham số m thỏa mãn yêu cầu.

Chọn đáp án A.

Ví dụ 5: Cho hàm số y = f(x) có đạo hàm là f(x) = (x - 2)2 . (x2 - x) (x là số thực). Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số $f\left( {\frac{1}{2}{x^2} - 6x + m} \right)$ có 5 điểm cực trị. Tìm tổng tất cả các phần tử của S.

A. 154

B. 17

C. 213

D. 153

Hướng dẫn giải

Ta có: Với x = 2 là nghiệm kép x = 0; x = 1 là nghiệm đơn. Do đó hàm số f(x) có hai điểm cực trị là x = 0; x = 1

Đặt $g(x)=f\left( {\frac{1}{2}{x^2} - 6x + m} \right)$ $\Rightarrow g'\left( x \right) = \left( {x - 6} \right)f'\left( {\frac{1}{2}{x^2} - 6x + m} \right)$

Khi đó g'(x) = 0 $\Rightarrow \left[ {\begin{array}{*{20}{c}} {x = 6} \\ {\dfrac{1}{2}{x^2} - 6x + m = 2} \\ {\dfrac{1}{2}{x^2} - 6x + m = 0\left( 1 \right)} \\ {\dfrac{1}{2}{x^2} - 6x + m = 1\left( 2 \right)} \end{array}} \right.$

Để hàm số có 5 điểm cực trị (1) và (2) có hai nghiệm phân biệt không trùng nhau và khác 6

Suy ra $\left\{ {\begin{array}{*{20}{c}} {{\Delta _1} 0} \\ {{\Delta _2} 0} \\ {\dfrac{1}{2}{{.6}^2} - 6.6 + m \ne 0} \\ {\dfrac{1}{2}{{.6}^2} - 6.6 + m \ne 1} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {9 - \dfrac{m}{2} 0} \\ {9 - \left( {\dfrac{{m - 1}}{2}} \right) 0} \\ {m \ne 18} \\ {m \ne 19} \end{array}} \right.$

=> m < 18

=> m ∈ {1; 2; 3; ...; 17}

Vậy tổng giá trị của m là 1 + 2 + 3 + ... + 17 = 153

Chọn đáp án D

---------------------------------------------------------------

Một số tài liệu liên quan:

Bài tập Thể tích hình trụ
Công thức tính thể tích hình nón
Công thức tính thể tích hình trụ
Xét tính chẵn lẻ của hàm số lượng giác
Phương trình lượng giác cơ bản
Bài toán tính tổng dãy số có quy luật Toán 11
Phương trình sinx=-1/2 có bao nhiêu nghiệm thuộc khoảng (-pi; pi)?
Phương trình căn 3 sin x cos x = 1 tương đương với phương trình nào sau đây?
Tìm tập xác định của hàm số lượng giác

Chia sẻ bởi:

Người Dơi Mời bạn đánh giá!

Lượt xem: 22.845

Tìm thêm: Toán 12 ôn thi thpt quốc gia 2024Sắp xếp theo Mặc địnhMới nhấtCũ nhất

Xóa Đăng nhập để Gửi

Tài liệu tham khảo khác

Tìm m để hàm số có 7 cực trị
Cực trị của hàm số

Chủ đề liên quan

Toán 12
Chuyên đề Toán 12

Mới nhất trong tuần

Công thức tính số cạnh, đỉnh của khối đa diện
Khối đa diện
Tìm m để hàm số có 5 cực trị
Cực trị của hàm số
Tìm m để hàm số đồng biến trên khoảng
Xét tính đơn điệu của hàm số
Tìm m để hàm số đồng biến trên R
Tính đơn điệu của hàm số
Khối đa diện đều loại {3; 3}
Tứ diện đều
Khối đa diện đều loại {3; 5}
Khối 20 mặt đều
Khối đa diện đều loại {3; 4}
Khối bát diện đều
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Tỉ số M/m thuộc khoảng nào?
GTLN - GTNN của hàm số
Cho hàm số y = - x³ + mx² - (m² + m + 1)x. Gọi S là tập hợp các giá trị của tham số m
GTLN - GTNN của hàm số
Gọi S là tập hợp tất cả các giá trị của tham số sao cho giá trị nhỏ nhất của hàm số
GTLN - GTNN của hàm số

Từ khóa » G(x)=f( X+m ) Có 5 điểm Cực Trị

Toán 1

Toán 2

Toán 3

Toán 4

Toán 5

Toán 6

Toán 7

Toán 8

Toán 9

Toán 10

Toán 11

Toán 12

Tìm m để hàm số có cực trị

Tìm m để hàm số có 5 điểm cực trị

Tài liệu tham khảo khác

Tìm m để hàm số có 7 cực trị

Chủ đề liên quan

Toán 12

Chuyên đề Toán 12

Mới nhất trong tuần

Công thức tính số cạnh, đỉnh của khối đa diện

Tìm m để hàm số có 5 cực trị

Tìm m để hàm số đồng biến trên khoảng

Tìm m để hàm số đồng biến trên R

Khối đa diện đều loại {3; 3}

Khối đa diện đều loại {3; 5}

Khối đa diện đều loại {3; 4}

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Tỉ số M/m thuộc khoảng nào?

Cho hàm số y = - x³ + mx² - (m² + m + 1)x. Gọi S là tập hợp các giá trị của tham số m

Gọi S là tập hợp tất cả các giá trị của tham số sao cho giá trị nhỏ nhất của hàm số

Liên Hệ