Tìm M để Hàm Số Có Tiệm Cận Ngang - Giải Toán 12
Có thể bạn quan tâm
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloTìm tham số m để hàm số có tiệm cận
- A. Cách tìm tiệm cận ngang
- B. Điều kiện để hàm số có tiệm cận ngang
- C. Công thức tính tiệm cận ngang của hàm phân thức hữu tỉ
- D. Công thức tính tiệm cận ngang của hàm phân thức vô tỷ
- D. Bài tập tìm tham số m để hàm số có tiệm cận ngang
Trong chương trình Toán 12, chuyên đề về đường tiệm cận của đồ thị hàm số là một nội dung quan trọng, thường xuyên xuất hiện trong các đề thi học kỳ và đặc biệt là kỳ thi THPT Quốc gia. Một trong những dạng bài hay gặp chính là yêu cầu tìm tham số m để hàm số có tiệm cận ngang. Đây là dạng toán vừa kiểm tra khả năng nắm vững kiến thức lý thuyết, vừa đánh giá kỹ năng biến đổi đại số và tư duy phân tích của học sinh.
Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách nhận biết tiệm cận ngang, điều kiện để hàm số có tiệm cận ngang và đặc biệt là cách tìm tham số m để hàm số có tiệm cận ngang một cách nhanh chóng và chính xác. Bên cạnh đó, bài viết còn cung cấp ví dụ minh họa chi tiết và hướng dẫn từng bước giải để giúp bạn nắm vững dạng toán này.
Tiệm cận ngang của đồ thị hàm số
Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
A. Cách tìm tiệm cận ngang
- Bước 1. Tìm tập xác định của hàm số.
- Bước 2. Tính các giới hạn của hàm số đó tại vô cực (nếu có). Từ đó xác định đường tιệm cận ngang.
B. Điều kiện để hàm số có tiệm cận ngang
- Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
![]() \(\lim_{x \rightarrow + \infty}f(x) = y_{0};\lim_{x \rightarrow - \infty}f(x) = y_{0}\)
\(\lim_{x \rightarrow + \infty}f(x) = y_{0};\lim_{x \rightarrow - \infty}f(x) = y_{0}\)
- Để tồn tại các đường tiệm cận của đồ thị hàm số
 \(y = \frac{ax + b}{cx + d}\) thì
\(y = \frac{ax + b}{cx + d}\) thì  \(\left\{ \begin{matrix} c \neq 0 \\ ad - bc \neq 0 \\ \end{matrix} \right.\)
\(\left\{ \begin{matrix} c \neq 0 \\ ad - bc \neq 0 \\ \end{matrix} \right.\) - Khi đó phương trình đường tiệm cận ngang là
 \(y = \frac{a}{c}\).
\(y = \frac{a}{c}\). - Điều kiện để đồ thị hàm số
 \(y = \frac{f(x)}{g(x)}\) có tiệm cận ngang là bậc f(x) không lớn hơn bậc của g(x).
\(y = \frac{f(x)}{g(x)}\) có tiệm cận ngang là bậc f(x) không lớn hơn bậc của g(x).
C. Công thức tính tiệm cận ngang của hàm phân thức hữu tỉ

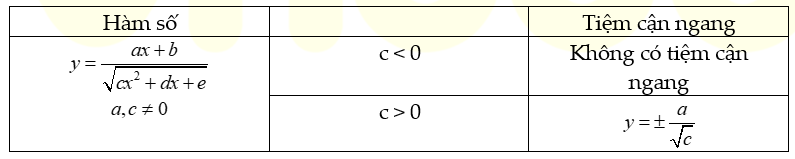
D. Công thức tính tiệm cận ngang của hàm phân thức vô tỷ
D. Bài tập tìm tham số m để hàm số có tiệm cận ngang
Bài tập 1: Tìm tất cả giá trị tham số m sao cho đồ thị hàm số ![]() \(y = \frac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{{x - 1}}\) có đúng hai tiệm cận ngang.
\(y = \frac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{{x - 1}}\) có đúng hai tiệm cận ngang.
| A. | B. |
| C. | D. |
Hướng dẫn giải
Để hàm số xác định trên ![]() \(\left( { - \infty ; + \infty } \right)\) thì
\(\left( { - \infty ; + \infty } \right)\) thì ![]() \(m - 1 \geqslant 0 \Leftrightarrow m \geqslant 1\)
\(m - 1 \geqslant 0 \Leftrightarrow m \geqslant 1\)
Ta có:
 \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{{x - 1}}\)
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{{x - 1}}\) \(= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\dfrac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{x}}}{{\dfrac{{x - 1}}{x}}} = 2 - \sqrt {m - 1}\)
\(= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\dfrac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{x}}}{{\dfrac{{x - 1}}{x}}} = 2 - \sqrt {m - 1}\)
![]() \(\Rightarrow y = 2 - \sqrt {m - 1}\) là tiệm cận ngang của đồ thị hàm số
\(\Rightarrow y = 2 - \sqrt {m - 1}\) là tiệm cận ngang của đồ thị hàm số
 \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{{x - 1}}\)
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{{x - 1}}\) \(= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{x}}}{{\dfrac{{x - 1}}{x}}} = 2 + \sqrt {m - 1}\)
\(= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{2x - \sqrt {\left( {m - 1} \right){x^2} + 1} }}{x}}}{{\dfrac{{x - 1}}{x}}} = 2 + \sqrt {m - 1}\)
![]() \(\Rightarrow y = 2 + \sqrt {m - 1}\) là tiệm cận ngang của đồ thị hàm số
\(\Rightarrow y = 2 + \sqrt {m - 1}\) là tiệm cận ngang của đồ thị hàm số
Để đồ thị có hai tiệm cận ngang ![]() \(\Leftrightarrow \sqrt {m - 1} \ne 0 \Leftrightarrow m \ne 1\)
\(\Leftrightarrow \sqrt {m - 1} \ne 0 \Leftrightarrow m \ne 1\)
Vậy m > 1
Đáp án D
Bài tập 2: Tìm tất cả giá trị tham số m sao cho đồ thị hàm số ![]() \(y = \frac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{{x + 1}}\) có đúng một tiệm cận ngang.
\(y = \frac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{{x + 1}}\) có đúng một tiệm cận ngang.
| A. | B. |
| C. | D. |
Hướng dẫn giải
Điều kiện xác định: ![]() \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
\(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
Ta có:
 \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{{x + 1}}\)
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{{x + 1}}\) \(= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\dfrac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{x}}}{{\dfrac{{x + 1}}{x}}} = \sqrt {{m^2} - 1}\)
\(= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\dfrac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{x}}}{{\dfrac{{x + 1}}{x}}} = \sqrt {{m^2} - 1}\)
 \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{{x + 1}}\)
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{{x + 1}}\) \(= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{x}}}{{\dfrac{{x + 1}}{x}}} = - \sqrt {{m^2} - 1}\)
\(= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{\sqrt {\left( {{m^2} - 1} \right){x^2} + x + 2} }}{x}}}{{\dfrac{{x + 1}}{x}}} = - \sqrt {{m^2} - 1}\)
Để đồ thị có duy nhất một tiệm cận ngang
 \(\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) \hfill \\ \Leftrightarrow \sqrt {{m^2} - 1} = - \sqrt {{m^2} - 1} \hfill \\ \Leftrightarrow m = \pm 1 \hfill \\ \end{matrix}\)
\(\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) \hfill \\ \Leftrightarrow \sqrt {{m^2} - 1} = - \sqrt {{m^2} - 1} \hfill \\ \Leftrightarrow m = \pm 1 \hfill \\ \end{matrix}\)
Đáp án C
Bài tập 3: Cho đồ thị hàm số ![]() \(y = \sqrt {m{x^2} + 2x} - x\). Tìm tất cả giá trị tham số m để đồ thị hàm số có tiệm cận ngang.
\(y = \sqrt {m{x^2} + 2x} - x\). Tìm tất cả giá trị tham số m để đồ thị hàm số có tiệm cận ngang.
| A. | B. |
| C. | D. |
Hướng dẫn giải
Ta có:
 \(y = \sqrt {m{x^2} + 2x} - x = \frac{{m{x^2} + 2x - {x^2}}}{{\sqrt {m{x^2} + 2x} + x}}\)
\(y = \sqrt {m{x^2} + 2x} - x = \frac{{m{x^2} + 2x - {x^2}}}{{\sqrt {m{x^2} + 2x} + x}}\) \(= \frac{{\left( {m - 1} \right){x^2} + 2x}}{{\sqrt {m{x^2} + 2x} + x}}\)
\(= \frac{{\left( {m - 1} \right){x^2} + 2x}}{{\sqrt {m{x^2} + 2x} + x}}\)
Đồ thị hàm số có tiệm cận ngang khi và chỉ khi bậc của tử bé hơn bậc của mẫu và tồn tại
![]() \(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m - 1 = 0} \end{array} \Leftrightarrow m = 1} \right.\)
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m - 1 = 0} \end{array} \Leftrightarrow m = 1} \right.\)
Đáp án A
Bài tập 4: Tìm giá trị của tham số m để đồ thị hàm số ![]() \(y = \frac{(2m - 1)x + 1}{x - m}\) có đường tiệm cận ngang là
\(y = \frac{(2m - 1)x + 1}{x - m}\) có đường tiệm cận ngang là ![]() \(y = 3\) ?
\(y = 3\) ?
Hướng dẫn giải
Điều kiện để đồ thị hàm số có tiệm cận là:
![]() \(- m(2m - 1) - 1 \neq 0 \Rightarrow 2m^{2} - m + 1 \neq 0\) luôn đúng với
\(- m(2m - 1) - 1 \neq 0 \Rightarrow 2m^{2} - m + 1 \neq 0\) luôn đúng với ![]() \(\forall x\mathbb{\in R}\)
\(\forall x\mathbb{\in R}\)
Phương trình đường tiệm cận ngang là ![]() \(y = 2m - 1\) nên ta có
\(y = 2m - 1\) nên ta có ![]() \(2x - 1 = 3 \Rightarrow m = 2\)
\(2x - 1 = 3 \Rightarrow m = 2\)
Bài tập 5: Cho hàm số ![]() \(y = 2x + \sqrt{mx^{2} - x + 1} + 1\) . Tìm giá trị của tham số
\(y = 2x + \sqrt{mx^{2} - x + 1} + 1\) . Tìm giá trị của tham số ![]() \(m\) sao cho đồ thị hàm số đã cho có tiệm cận ngang?
\(m\) sao cho đồ thị hàm số đã cho có tiệm cận ngang?
Hướng dẫn giải
Ta có:
 \(\begin{matrix} y = (2x + 1) + \sqrt {m{x^2} - x + 1} \hfill \\ \Rightarrow y = \dfrac{{4{x^2} + 4x + 1 - \left( {m{x^2} - x + 1} \right)}}{{2x + 1 - \sqrt {m{x^2} - x + 1} }} \hfill \\ \Rightarrow y = \dfrac{{(4 - m){x^2} + 5x}}{{2x + 1 - \sqrt {m{x^2} - x + 1} }} \hfill \\ \end{matrix}\)
\(\begin{matrix} y = (2x + 1) + \sqrt {m{x^2} - x + 1} \hfill \\ \Rightarrow y = \dfrac{{4{x^2} + 4x + 1 - \left( {m{x^2} - x + 1} \right)}}{{2x + 1 - \sqrt {m{x^2} - x + 1} }} \hfill \\ \Rightarrow y = \dfrac{{(4 - m){x^2} + 5x}}{{2x + 1 - \sqrt {m{x^2} - x + 1} }} \hfill \\ \end{matrix}\)
Đồ thị hàm số có tiệm cận ngang khi và chỉ khi bậc của tử số bé hơn hoặc bằng bậc của mẫu số
Đồng thời ![]() \(\lim_{x \rightarrow \infty}y = y_{0} \Rightarrow \left\{ \begin{matrix} m > 0 \\ 4 - m = 0 \\ \end{matrix} \Rightarrow m = 4 \right.\)
\(\lim_{x \rightarrow \infty}y = y_{0} \Rightarrow \left\{ \begin{matrix} m > 0 \\ 4 - m = 0 \\ \end{matrix} \Rightarrow m = 4 \right.\)
Bài tập 6: Tìm tất cả các giá trị thực của tham số ![]() \(m\) để đồ thị hàm số
\(m\) để đồ thị hàm số ![]() \(y = \frac{x + 2}{x^{2} - 4x + m}\) có đúng một tiệm cận ngang và đúng một tiệm cận đứng.
\(y = \frac{x + 2}{x^{2} - 4x + m}\) có đúng một tiệm cận ngang và đúng một tiệm cận đứng.
A. ![]() \(m < 4.\) B.
\(m < 4.\) B. ![]() \(m > 4.\)
\(m > 4.\)
C. ![]() \(m = 4,m = - 12.\) D.
\(m = 4,m = - 12.\) D. ![]() \(m \neq 4.\)
\(m \neq 4.\)
Hướng dẫn giải
Ta có ![]() \(\lim_{x \rightarrow \pm \infty}\frac{x + 2}{x^{2} - 4x + m} = 0 \rightarrow y = 0\) là tiệm cận ngang với mọi
\(\lim_{x \rightarrow \pm \infty}\frac{x + 2}{x^{2} - 4x + m} = 0 \rightarrow y = 0\) là tiệm cận ngang với mọi ![]() \(m.\)
\(m.\)
Để đồ thị hàm số ![]() \(y = \frac{x + 2}{x^{2} - 4x + m}\) có đúng một tiệm cận ngang và đúng một tiệm cận đứng
\(y = \frac{x + 2}{x^{2} - 4x + m}\) có đúng một tiệm cận ngang và đúng một tiệm cận đứng ![]() \(\Leftrightarrow\)Phương trình
\(\Leftrightarrow\)Phương trình ![]() \(x^{2} - 4x + m = 0\) có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng
\(x^{2} - 4x + m = 0\) có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng ![]() \(- 2\)
\(- 2\)
 \(\Leftrightarrow \left\lbrack \begin{matrix} \Delta' = 4 - m = 0 \\ \left\{ \begin{matrix} \Delta' = 4 - m > 0 \\ ( - 2)^{2} - 4( - 2) + m = 0 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} m = 4 \\ m = - 12 \\ \end{matrix} \right.\)
\(\Leftrightarrow \left\lbrack \begin{matrix} \Delta' = 4 - m = 0 \\ \left\{ \begin{matrix} \Delta' = 4 - m > 0 \\ ( - 2)^{2} - 4( - 2) + m = 0 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} m = 4 \\ m = - 12 \\ \end{matrix} \right.\)
Bài tập 7: Tìm tất cả các giá trị của tham số ![]() \(m\) để đồ thị hàm số
\(m\) để đồ thị hàm số ![]() \(y = \frac{x + 2}{x^{2} - 4x + m}\) có tiệm cận ngang mà không có tiệm cận đứng.
\(y = \frac{x + 2}{x^{2} - 4x + m}\) có tiệm cận ngang mà không có tiệm cận đứng.
A. ![]() \(m = - 12.\) B.
\(m = - 12.\) B. ![]() \(m > 4.\) C.
\(m > 4.\) C. ![]() \(m = - 12,m > 4.\) D.
\(m = - 12,m > 4.\) D. ![]() \(m \neq 4.\)
\(m \neq 4.\)
Hướng dẫn giải
Ta có ![]() \(\lim_{x \rightarrow \pm \infty}\frac{x + 2}{x^{2} - 4x + m} = 0y = 0\) là tiệm cận ngang với mọi
\(\lim_{x \rightarrow \pm \infty}\frac{x + 2}{x^{2} - 4x + m} = 0y = 0\) là tiệm cận ngang với mọi ![]() \(m\).
\(m\).
Do đó để đồ thị hàm số có tiệm cận ngang mà không có tiệm cận đứng thì phương trình ![]() \(x^{2} - 4x + m = 0\) vô nghiệm
\(x^{2} - 4x + m = 0\) vô nghiệm
Từ khóa » Hàm Số Có 2 Tiệm Cận Ngang Khi Nào
-
Bài Tập Tìm M để Hàm Số Có Tiệm Cận đứng, Tiệm Cận Ngang Có đáp án
-
Bài Tập Tìm M để Hàm Số Có Tiệm Cận đứng - Tự Học 365
-
Tiệm Cận Ngang Của đồ Thị Hàm Số - Toán Thầy Định
-
Tìm M để Hs Y=(x+1)/ Căn(mx^2+1) Có 2 Tiệm Cận Ngang - Hoc247
-
Tiệm Cận Ngang Là Gì? Cách Tìm Tiệm Cận Ngang Của Đồ Thị ...
-
Cách Tìm Tiệm Cận đứng Và Tiệm Cận Ngang Của Hàm Số
-
Đường Tiệm Cận Của Hàm Số: Lý Thuyết & Bài Tập (Kèm Tài Liệu)
-
Lý Thuyết đường Tiệm Cận Của đồ Thị Hàm Số Và Luyện Tập Toán 12
-
Tiệm Cận Ngang Của đồ Thị Hàm Số Là Gì? Cách Xác định đường Tiệm ...
-
Tìm M để đồ Thị Hàm Số Có đúng 2 Tiệm Cận - Blog Của Thư
-
Bài Giảng Toán 12 - DS_C1_TIEM ml
-
Tìm M Để Hàm Số Có 2 Tiệm Cận Đứng, Tiệm Cận Ngang Có Đáp ...
-
Tìm Tham Số M để Hàm Số Có Tiệm Cận Cực Hay - Toán Lớp 12
-
[DOC] I._Tom_tat_ly_thuyet_c