Tìm M để Hàm Số đồng Biến, Nghịch Biến Trên Khoảng

Tìm m để hàm số đồng biến, nghịch biến trên khoảng Xét tính đơn điệu của hàm số Toán 12 có đáp án Bài trước Tải về Bài sau Lớp: THPT Quốc gia Môn: Toán Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Tìm m để hàm số đồng biến, nghịch biến trên khoảng

• I. Phương pháp giải bài toán tìm m để hàm số đồng biến, nghịch biến trên khoảng
• II. Ví dụ minh họa tìm m để hàm số đồng biến, nghịch biến trên khoảng cho trước.
• II. Bài tập tự luyện
• Lịch thi THPT Quốc Gia 2023

Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

I. Phương pháp giải bài toán tìm m để hàm số đồng biến, nghịch biến trên khoảng

- Định lí: Cho hàm số  \(y=f\left( x \right)\) có đạo hàm trên khoảng \(\left( a,b \right)\):

+ Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \(\left( a,b \right)\) khi và chỉ khi \(\left( 0,+\infty \right)\Leftrightarrow y'\le 0\) với mọi \(x\in \left( 0,+\infty \right)\)

\(\Leftrightarrow -3{{x}^{2}}+6x+3m\le 0,\forall x\in \left( 0,+\infty \right)\Leftrightarrow m\le {{x}^{2}}-2x,\forall x\in \left( 0,+\infty \right)\)

Xét \(f\left( x \right)={{x}^{2}}-2x\) với \(\Leftrightarrow y' \geq 0;\forall x \in \lbrack 1; + \infty)\)

\(\Leftrightarrow x^{2} + mx + 1 \geq 0;\forall x \in \lbrack 1; + \infty)\)

\(\Leftrightarrow m \geq - x - \frac{1}{x};\forall x \in \lbrack 1; + \infty)\)

Xét hàm số \(g(x) = - x - \frac{1}{x}\) trên nửa khoảng \(\lbrack 1; + \infty)\) ta có:

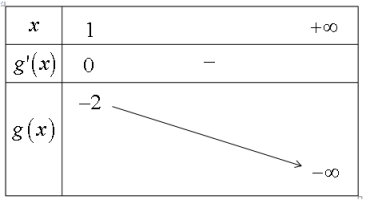\(y' \leq 0;\forall x \in (0; + \infty)\) khi và chỉ khi

\(\Leftrightarrow 2m \leq 3x^{2} - 6x + 1;\forall x \in (0; + \infty)\)

Xét hàm số \(g() = 3x^{2} - 6x + 1\) trên \((0; + \infty)\) ta có bảng biến thiên như sau:

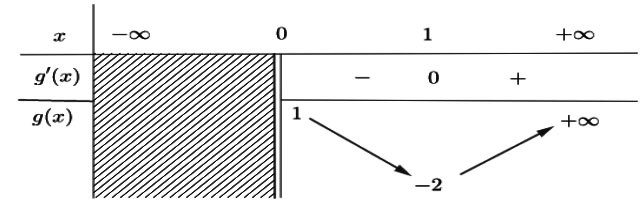
Dựa vào bảng biến thiên ta có:

\(\min_{(0; + \infty)}g(x) = - 2\)

Do đó \(\Leftrightarrow 2m \leq \min_{(0; + \infty)}g(x) \Leftrightarrow 2m \leq - 2 \Leftrightarrow m \leq - 1\)

Vậy \(m \leq - 1\) thỏa mãn yêu cầu bài toán.

Ví dụ 6. Cho hàm số \(y = \frac{m^{2}x + 5}{2mx + 1}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các số nguyên \(m \in \lbrack - 2020;2020\rbrack\) để hàm số đã cho nghịch biến trên khoảng \((3; + \infty)\). Xác định số phần tử của tập hợp \(S\)?

Hướng dẫn giải

Xét \(m = 0 \Rightarrow y = 5\) là hàm hằng nên hàm số không nghịch biến. Vậy \(m = 0\) không thỏa mãn.

Xét \(m \neq 0\)

Tập xác định \(D = \left( - \infty; - \frac{1}{2m} \right) \cup \left( - \frac{1}{2m}; + \infty \right)\)

Để hàm số nghịch biến trên khoảng \((3; + \infty)\) khi và chỉ khi

\(\left\{ \begin{matrix} y' = \frac{m^{2} - 10m}{(2mx + 1)^{2}} < 0 \\ - \frac{1}{2m} \leq 3 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} - 10m < 0 \\ \frac{6m + 1}{2m} \geq 0 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} 0 < m < 10 \\ \left\lbrack \begin{matrix} m \leq - \frac{1}{6} \\ m > 0 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow 0 < m < 10\)

Mà \(\left\{ \begin{matrix} m\mathbb{\in Z} \\ m \in \lbrack - 2020;2020\rbrack \\ \end{matrix} \right.\) nên \(m \in \left\{ 1;2;3;...;9 \right\}\)

Vậy tập hợp S có tất cả 9 giá trị.

Ví dụ. Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \frac{1}{3}(m + 2)x^{3} - (m + 2)x^{2} + (m - 8)x + m^{2} - 1\) luôn nghịch biến trên \(\mathbb{R}\)?

Hướng dẫn giải

Với \(m = - 2\) ta có \(y = - 10x + 3\) (hàm số này luôn nghịch biến trên tập số thực)

Với \(m \neq - 2\) ta có \(y' = (m + 2)x^{2} - 2(m + 2)x + m - 8\)

Hàm số nghịch biến trên