Tìm Nguyên Hàm Của Hàm Số F( X )=sin 2x. - Sách Toán - Học Toán

Trang chủ » Nguyên Hàm X/sin^2x » Tìm Nguyên Hàm Của Hàm Số F( X )=sin 2x. - Sách Toán - Học Toán

Có thể bạn quan tâm

Câu hỏi: Tìm nguyên hàm của hàm số f( x )=sin 2x.

A. \( \smallint \sin 2x{\mkern 1mu} {\rm{d}}x = – \frac{{\cos 2x}}{2} + C.\) B. \( \smallint \sin 2x{\mkern 1mu} {\rm{d}}x = – \cos 2x + C.\) C. \( \smallint \sin 2x{\mkern 1mu} {\rm{d}}x = \frac{{\cos 2x}}{2} + C.\) D. \( \smallint \sin 2x{\mkern 1mu} {\rm{d}}x =2 \cos 2x + C.\)

Lời Giải: Đây là các câu trắc nghiệm về NGUYÊN HÀM mức độ 1,2 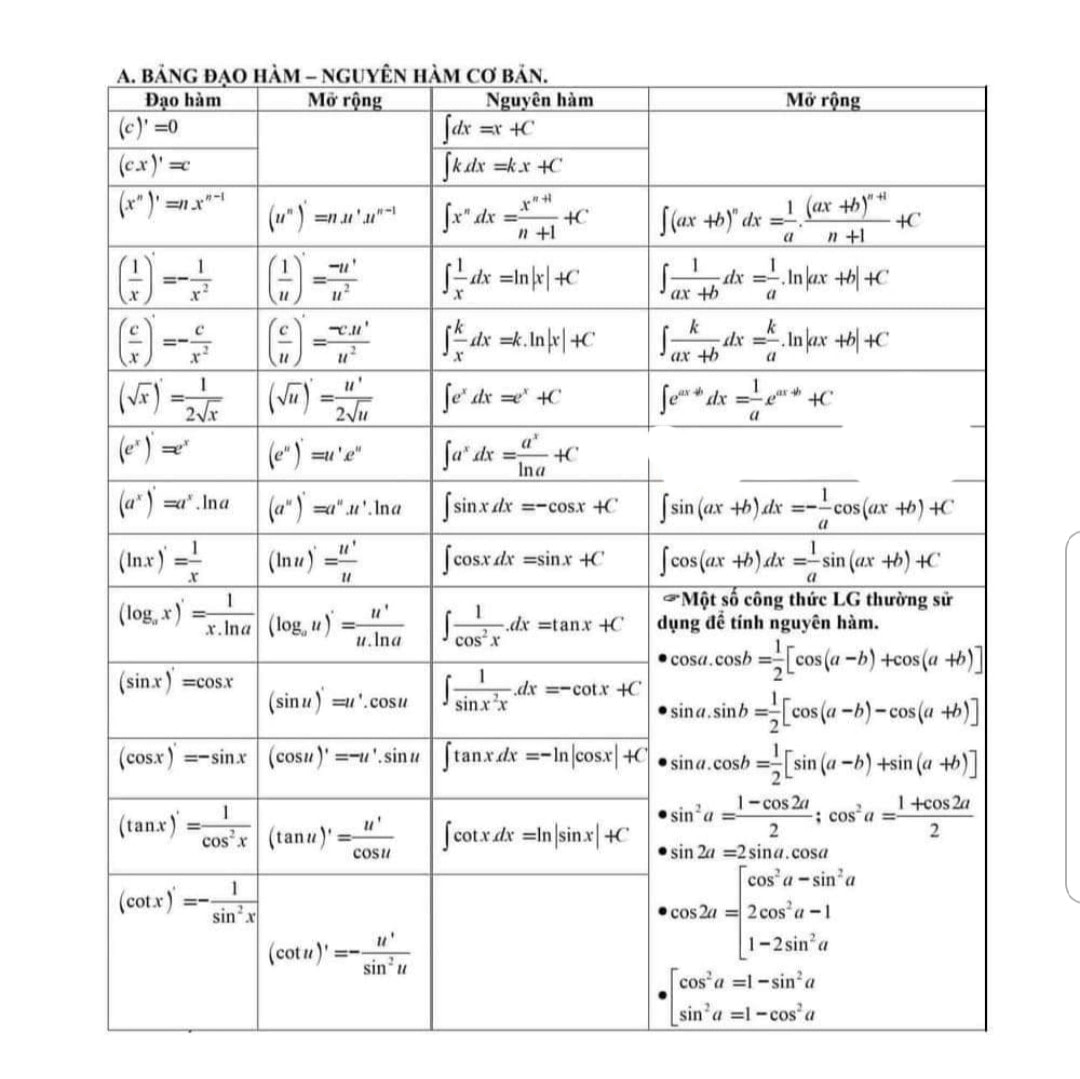Tìm nguyên hàm của hàm số f( x )=sin 2x. 1

Ta có

\( \smallint \sin 2x{\mkern 1mu} {\rm{d}}x = – \frac{{\cos 2x}}{2} + C.\)

===============

==================== Thuộc chủ đề: Trắc nghiệm Nguyên hàm

Từ khóa » Nguyên Hàm X/sin^2x