Tìm Số Hạng Chứa X ^7 Trong Khai Triển (x-1/x)^13 ....

Trang chủ » Hệ Số X2 Trong Khai Triển (1+2x)^12 » Tìm Số Hạng Chứa X ^7 Trong Khai Triển (x-1/x)^13 ....

Có thể bạn quan tâm

Đăng nhập Facebook GOOGLE Google IMG

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

23/07/2024 78,147

Tìm số hạng chứa x7 trong khai triển (x−1x)13.

A. −C134x7

B. −C133

C. −C133x7

Đáp án chính xác

D. C133x7

Xem lời giải Xem lý thuyết Câu hỏi trong đề: Trắc nghiệm Nhị thức newton có đáp án Bắt Đầu Thi Thử

Trả lời:

verified Giải bởi Vietjack

VietJack

VietJack

Câu trả lời này có hữu ích không?

9 10

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Hệ số của số hạng chứa x5 trong khai triển (x+1)10 là

Xem đáp án » 31/07/2021 17,549

Câu 2:

Tìm số hạng không chứa x trong khai triển x2+2x6 .

Xem đáp án » 31/07/2021 16,290

Câu 3:

Tìm số hạng không chứa x trong khai triển xy2−1xy8 .

Xem đáp án » 31/07/2021 10,265

Câu 4:

Trong khai triển 3x2+1xn hệ số của x3 là: 34 Cn5 giá trị của n là:

Xem đáp án » 01/08/2021 7,973

Câu 5:

Tìm hệ số của x12 trong khai triển (2x−x2)10

Xem đáp án » 31/07/2021 7,856

Câu 6:

Trong khai triển (x-y)11 , hệ số của số hạng chứa x8y3 là:

Xem đáp án » 01/08/2021 6,270

Câu 7:

Tổng của số hạng thứ 4 trong khai triển (5a-1)5 và số hạng thứ 5 trong khai triển (2a-3)6 là:

Xem đáp án » 01/08/2021 5,629

Câu 8:

Trong khai triển (1+3x)20 với số mũ tăng dần, hệ số của số hạng đứng chính giữa là:

Xem đáp án » 01/08/2021 4,358

Câu 9:

Khai triển nhị thức (x+2)n+5(n∈N) có tất cả 2019 số hạng. Tìm n.

Xem đáp án » 31/07/2021 2,994

Câu 10:

Cho khai triển (x+2y)8. Hỏi khai triển trên có tất cả bao nhiêu số hạng?

Xem đáp án » 01/08/2021 2,061

Câu 11:

Nếu bốn số hạng đầu của một hàng trong tam giác Pascal được ghi lại là:

1 16 120 560

Khi đó 4 số hạng đầu của hàng kế tiếp là:

Xem đáp án » 01/08/2021 594

Câu 12:

Trong khai triển a2−1b7=C70a14+...+C77−1b7 , số hạng thứ 5 là

Xem đáp án » 31/07/2021 541

Câu 13:

Giá trị của biểu thức S=999C990+998C991+997C992+...+9C9998+C9999 bằng:

Xem đáp án » 31/07/2021 493

Câu 14:

Giá trị của biểu thức S=399C990+398.4.A991+397.42.C992+...+3.498C9998+499C9999 bằng:

Xem đáp án » 31/07/2021 406 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

I. Công thức nhị thức Niu- tơn

Ta có:

a+ b2= a2+​ 2ab+  b2= C20a2+​ C21.a1b1  +  C22b2a-b3= a3+​ 3a2b +​3ab2​+ b3  =  C30.a3  + C31a2b1​+​  C32a1b2+​  C33b3

- Công thức nhị thức Niu – tơn.

(a​  +  b)n  =  Cn0an  +​  Cn1.an−1b+​ ...+​  Cnk.an−kbk ​+​....+​Cnn−1abn−1+​  Cnnbn

- Hệ quả:

Với a = b = 1 ta có: 2n  = Cn0 +​ Cn1 +​...​+​ Cnn

Với a = 1; b = – 1 ta có: 0  = Cn0 −​ Cn1 +​...+​(−1)k.Cnk+​...​+(−1)n​ Cnn

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước a0=b0=1).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

- Ví dụ 1. Khai triển biểu thức: (a – b)^5.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

Invalid <m:msup> element  =  C50a5  +​  C51.a4(−b)+Invalid <m:msup> element​  C52.Invalid <m:msup> elementa3 ​+Invalid <m:msup> element​C53Invalid <m:msup> elementa2+​  C54a+ C55=  a5  − 5a4b  +  ​10a3b2−10a2b3+​  5ab4− b5

- Ví dụ 2. Khai triển biểu thức: (3x – 2)^4.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

Invalid <m:msup> element  = Invalid <m:msup> element C40  +​Invalid <m:msup> element  C41.(−2)Invalid <m:msup> elementInvalid <m:msup> element+​  C42.Invalid <m:msup> element ​+​C43Invalid <m:msup> element(3x)+​  C44=  81x4−216x3+  ​216x2−96x+16

II. Tam giác Pa- xcan

Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.

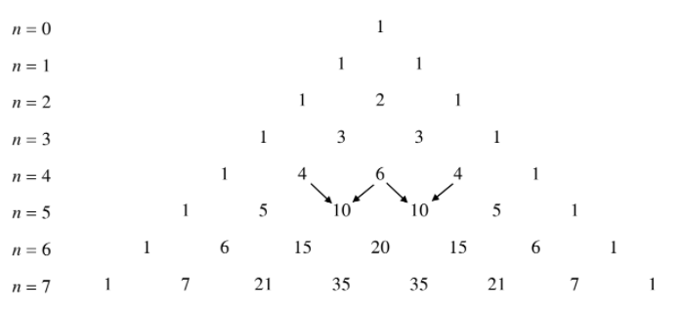
Bài 3: Nhị thức Niu-tơn (ảnh 1)

- Nhận xét:

Từ công thức Cnk =  Cn−1k−1  +  Cn−1k suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.

Ví dụ 3. C62=C51+C52=5+10=15.

Đề thi liên quan

Xem thêm »
  • Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 22949 lượt thi Thi thử
  • Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 8267 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 4836 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 4059 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 3782 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 3715 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 3198 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 3132 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 3064 lượt thi Thi thử
  • Trắc nghiệm Biến cố và xác suất của biến cố có đáp án 4 đề 3042 lượt thi Thi thử
Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?

    Một vòng quay trò chơi có bán kính 57 m Khi quay một vòng lần thứ nhất tính từ (ảnh 1) 249 18/04/2024 Xem đáp án

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

    Một vòng quay trò chơi có bán kính 57 m Khi t = 0 (phút) thì khoảng cách từ cabin (ảnh 1) 137 18/04/2024 Xem đáp án

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Tính chu kì của hàm số h(t)?

    Một vòng quay trò chơi có bán kính 57 m Tính chu kì của hàm số h(t) (ảnh 1) 120 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = sin x, tìm:

    Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương. 127 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = sin x, tìm:

    Các giá trị của x để sin x = \(\frac{1}{2}\);

    120 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = cos x, cho biết:

    Có bao nhiêu giá trị của x trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để cos x = 0.

    114 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = cos x, cho biết:

    Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;

    117 18/04/2024 Xem đáp án

  • Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

    y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).

    120 18/04/2024 Xem đáp án

  • Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

    y = sin x trên khoảng \(\left( { - \frac{{19\pi }}{2};\, - \frac{{17\pi }}{2}} \right),\,\,\left( { - \frac{{13\pi }}{2};\, - \frac{{11\pi }}{2}} \right)\);

    119 18/04/2024 Xem đáp án

  • Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

    \(y = \frac{1}{{4 - \sin x}}\).

    125 18/04/2024 Xem đáp án
Xem thêm »

Từ khóa » Hệ Số X2 Trong Khai Triển (1+2x)^12