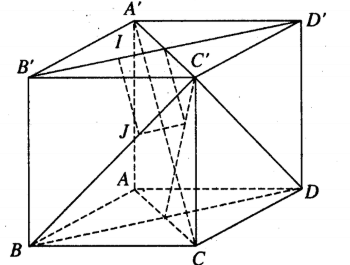
Tìm Tọa độ Của Chân đường Vuông Góc Chung Của B'D' Và BC'

Từ khóa » Tìm Tọa độ Chân đường Vuông Góc

• 3) : B(2;-1) Và C(-1; 5). Tính Tọa độ Chân đường Cao - Khóa Học

• 5) Và B(-2;8) Và C(6;9) Tìm Tọa độ điểm H Là Chân Của đường Cao Vẽ ...

• Tìm Tọa độ Chân đường Cao Của Tam Giác - Bùi Tuấn Anh - Học Để Thi

• Tìm Tọa độ Của Chân đường Vuông Góc Chung Của ...

• Tìm Tọa độ Chân đường Cao Hạ Từ đỉnh A Của Tam Giác ABC

• Trong Mặt Phẳng Tọa độ (Oxy, ) Cho Tam Giác (ABC ) Có (A( (4;3

• 7 ); C(3;8). Tìm Toạ độ Chân đường Cao Kẻ Từ đỉnh A Xuống BC - Hoc24

• Tìm Tọa độ Của Chân đường Vuông Góc Chung Của B'D' Và BC ...

• Gọi điểm E(3; 1) Là Chân đường Vuông Góc Hạ Từ B Xuống AI - Hoc247

• Tìm Tọa Độ Chân Đường Cao - Hạ Từ Đỉnh A Của Tam Giác Abc

• Tính Tọa độ Chân đường Cao Của Tam Giác Kẻ Từ A Biết A(1;2 ), B(3

• Cho Tam Giác ABC Nội Tiếp đường Tròn Tâm I, Có đỉnh A Thuộc ... - Olm

• Trong Mặt Phẳng Với Hệ Tọa độ Oxy Cho Tam Giác ABC Nội Tiếp ... - Olm