Toán 10 Bài 3: Các Phép Toán Tập Hợp

Toán 10 Bài 3: Các phép toán tập hợpLý thuyết, bài tập Toán 10Bài trướcTải vềBài sauNâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Giải Toán 10 Bài Các phép toán trên tập hợp

• Giải Toán 10 bài Các phép toán trên tập hợp sách mới
  • Giải Toán 10 Bài Các phép toán trên tập hợp sách Chân trời sáng tạo
  • Giải Toán 10 Bài Tập hợp và các phép toán trên tập hợp sách Kết nối tri thức
  • Giải Toán 10 Bài Tập hợp và các phép toán trên tập hợp sách Cánh Diều
• Giải Toán 10 bài 3 sách giáo khoa cũ
  • A. Lí thuyết Các phép toán tập hợp
  • B. Giải SGK Toán 10 Bài 3
  • C. Giải SBT Toán 10 Bài 3
  • D. Bài tập trắc nghiệm Toán 10 Các phép toán tập hợp
  • E. TÀI LIỆU HỌC TẬP SGK TOÁN 10 MỚI

Toán 10 Bài 3: Các phép toán trên tập hợp được VnDoc biên soạn tổng hợp gồm có hướng dẫn giải bài tập SGK Toán 10 của 3 bộ sách theo chương trình giáo dục phổ thông mới. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Giải Toán 10 bài Các phép toán trên tập hợp sách mới

Giải Toán 10 Bài Các phép toán trên tập hợp sách Chân trời sáng tạo

Bài 1 trang 25 Toán 10 CTST Tập 1 

Xác định các tập hợp A ∪ B và A ∩ B với:

a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím};

b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.

Lời giải

a) Tập A ∪ B = {đỏ; cam; vàng; lục; lam; chàm; tím}.

Các phần tử vừa thuộc tập hợp A và B là: lục; lam.

Do đó A ∩ B = {lục; lam}.

Vậy A ∪ B = {đỏ; cam; vàng; lục; lam; chàm; tím} và A ∩ B = {lục; lam}.

b) Vì mọi tam giác đều là tam giác cân nên tập A là tập hợp con của B.

Khi đó A ∪ B = B và A ∩ B = A.

Vậy A ∪ B = B và A ∩ B = A.

Bài 2 trang 25 SGK Toán 10 CTST Tập 1

Xác định tập hợp A ∩ B trong mỗi trường hợp sau:

a) A = {x ∈ ℝ | x2 – 2 = 0}, B = {x ∈ ℝ | 2x – 1 < 0};

b) A = {(x; y)| x, y ∈ ℝ , y = 2x – 1}, B = {(x; y)| x, y ∈ ℝ, y = - x + 5};

c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.

Lời giải

a) Xét phương trình: x2 – 2 = 0 ⇔ \(\left\{\begin{array}{l}x\;=-\sqrt2\\x\;=\;\sqrt2\end{array}\right.\)

=> A = \(\left(-\sqrt{2;\;}\sqrt2\right)\)

Xét bất phương trình 2x – 1 < 0 ⇔ x < \(\frac12\)

⇒B={x∈R∣x<\(\frac12\)}

Ta có −√2<\(\frac12\) và √2>\(\frac12\) nên −√2∈B,√2∉B

Do đó A ∩ B = {−√2}

Vậy A ∩ B = {−√2}

b) Ta có: A ∩ B = {(x; y)| x, y ∈ ℝ, y = 2x – 1, y = -x + 5}

Các cặp (x; y) thuộc tập hợp A ∩ B thỏa mãn y = 2x – 1, y = -x + 5 (x, y ∈ ℝ)

Xét phương trình hoành độ giao điểm 2x – 1 = -x + 5

⇔ 2x + x = 5 + 1

⇔ 3x = 6

⇔ x = 2

⇒ y = - 2 + 5 = 3

Do đó A ∩ B = {(2; 3)}.

Vậy A ∩ B = {(2; 3)}.

c) Hình thoi không là hình chữ nhật và hình chữ nhật cũng không là hình thoi. Nhưng hình vuông vừa là hình thoi vừa là hình chữ nhật.

Do đó A ∩ B là tập hợp các hình vuông.

Vậy A ∩ B là tập các hình vuông.

Bài 3 trang 25 SGK Toán 10 CTST Tập 1

Cho E = {x ∈ ℕ | x < 10}, A = {x ∈ E| x là bội của 3}, B = {x ∈ E| x là ước của 6}. Xác định các tập hợp A\B, B\A, CEA, CEB, CE(A∪B), CE(A∩B).

Lời giải

Tập hợp E là tập các số tự nhiên nhỏ hơn 10 nên E = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.

Trong tập hợp E, các số là bội của 3 là: 0; 3; 6; 9. Khi đó A = {0; 3; 6; 9}.

Trong tập hợp E, các số là ước của 6 là: 1; 2; 3; 6. Khi đó B = {1; 2; 3; 6}.

Các tập hợp đã cho được xác định như sau:

- Tập hợp A\B là tập các phần tử thuộc tập A không thuộc tập hợp B nên A\B = {0; 9}.

- Tập hợp B\A là tập các phần tử thuộc tập B không thuộc tập hợp A nên B\A = {1; 2}.

- Tập hợp CEA là tập hợp phần bù của tập E và A nên CEA = {1; 2; 4; 5; 7; 8}.

- Tập hợp CEB là tập hợp phần bù của tập E và B nên CEB = {0; 4; 5; 7; 8; 9}.

Ta có A∪B = {0; 1; 2; 3; 6; 9}, A∩B = {3; 6}

- Tập hợp CE(A∪B) là tập hợp phần bù của tập A∪B trong E nên CE(A∪B) = {4; 5; 7; 8}.

- Tập hợp CE(A∩B) là tập hợp phần bù của tập A∩B trong E nên CE(A∩B) = {0; 1; 2; 4; 5; 7; 8; 9}.

Bài 4 trang 25 SGK Toán 10 CTST Tập 1

Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.

a) A và A∪B;

b) A và A∩B.

Lời giải

Ta có sơ đồ ven sau:

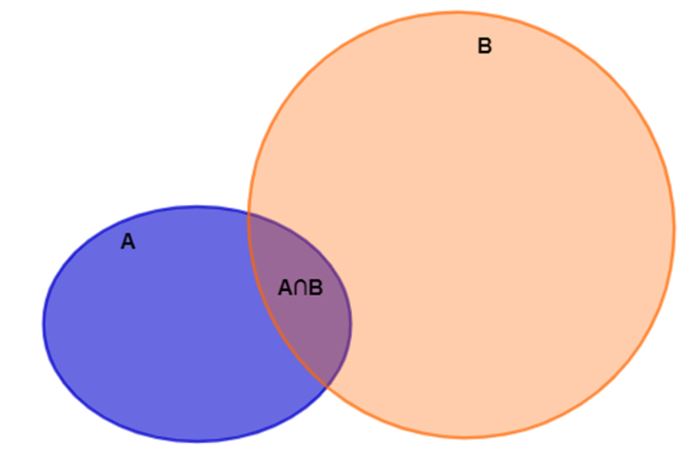
Ta thấy tập hợp A ∪ B bao gồm phần màu xanh, phần màu tím và phần màu cam.

Tập hợp A chứa phần màu xanh cộng màu tím nằm hoàn toàn trong tập hợp A ∪ B. Do đó tập A là tập con của tập A ∪ B. Ta viết A ⊂ (A∪B).

Tập hợp A∩B là phần màu tím và nằm hoàn toàn trong tập hợp A nên tập A∩B là tập con của tập A. Ta viết (A∩B) ⊂ A.

Bài 5 trang 25 SGK Toán 10 CTST Tập 1

Trong số 35 học sinh của lớp 10H, có 20 học sinh thích học môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:

a) có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?

b) có bao nhiêu học sinh không thích cả hai môn này?

Lời giải

Ta có sơ đồ ven:

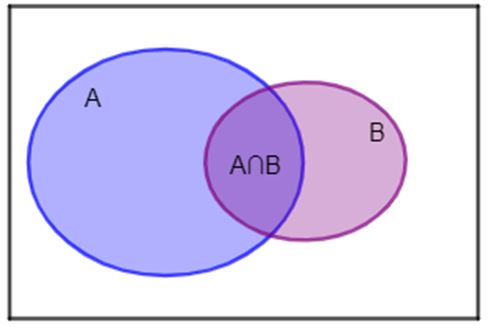
a) Gọi A là tập hợp học sinh của lớp 10H thích học môn Toán, B là tập hợp học sinh của lớp 10H thích học môn Tiếng Anh.

Theo giả thiết, n(A) = 20, n(B) = 16, n(A∩B) = 12.

Nhận thấy rằng, nếu tính tổng n(A) + n(B) thì ta được số học sinh lớp 10H thích môn Toán hoặc Tiếng Anh, nhưng số bạn thích cả hai môn được tính hai lần. Do đó, số bạn học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:

n(A∪B) = n(A) + n(B) – n(A∩B) = 20 + 16 – 12 = 24.

Vậy lớp 10H có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh.

b) Số học sinh của lớp 10H không thích cả hai môn Toán và Tiếng Anh là:

35 – 24 = 11 (học sinh).

Vậy có 11 học sinh của lớp 10H không thích cả hai môn Toán và Tiếng Anh.

Bài 6 trang 25 SGK Toán 10 CTST Tập 1

Xác định các tập hợp sau đây:

a) (−∞;0]∪[−π;π];

b) [-3,5; 2] ∩ (-2; 3,5);

c) (−∞;√2]∩[1;+∞);

d) (−∞;√2]\[1;+∞) .

Lời giải

Giải Toán 10 Bài Tập hợp và các phép toán trên tập hợp sách Kết nối tri thức

Bài 1.8 trang 19 SGK Toán 10 KNTT

Gọi X là tập hợp các quốc gia tiếp giáp với Việt Nam. Hãy liệt kê các phần tử của tập hợp X và biểu diễn tập X bằng sơ đồ Ven.

Lời giải

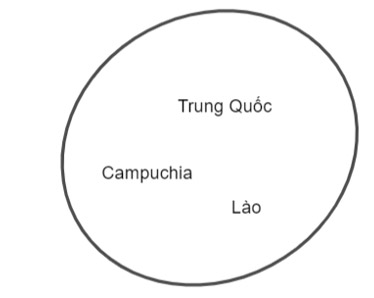
Các quốc gia tiếp giáp với Việt Nam bao gồm: Trung Quốc, Lào, Campuchia.

⇒ X = {Trung Quốc, Lào, Campuchia}.

Biểu diễn tập hợp X bằng sơ đồ Ven, ta được:

Bài 1.9 trang 19 SGK Toán 10 KNTT

Kí hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á.

a) Nêu ít nhất hai phần tử thuộc tập hợp E.

b) Nêu ít nhất hai phần tử không thuộc tập hợp E.

c) Liệt kê các phần tử thuộc tập hợp E. Tập hợp E có bao nhiêu phần tử?

Lời giải

a) Các phần tử thuộc tập hợp E là: Việt Nam, Singapore, Lào.

b) Các phần tử không thuộc tập hợp E là: Mĩ, Nga, Anh.

c) Các quốc gia tại khu vực Đông Nam Á bao gồm: Việt Nam, Lào, Campuchia, Thái Lan, Myanmar, Malaysia, Singapore, Indonesia, Brunei, Philippines và Đông Timor.

Khi đó tập hợp E = {Việt Nam, Lào, Campuchia, Thái Lan, Myanmar, Malaysia, Singapore, Indonesia, Brunei, Philippines, Đông Timor}.

Tập hợp E có tất cả 11 phần tử.

Bài 1.10 trang 19 SGK Toán 10 KNTT

Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp:

A = {0; 4; 8; 12; 16}.

Lời giải

Bằng cách nêu tính chất đặc trưng:

A = {x ∈ ℕ | x = 4k, x < 18, k ∈ ℕ}.

Bài 1.11 trang 19 SGK Toán 10 KNTT

Trong các tập hợp sau, tập nào là tập rỗng?

A = { x ∈ ℝ | x2 – 6 = 0};

B = { x ∈ ℤ | x2 – 6 = 0};

Lời giải

Ta có: x2 – 6 = 0

⇔\(\left\{\begin{array}{l}x=\surd6\\x=-\surd6\end{array}\right.\)

Vì −√6; √6 ∈ R nên A = {−√6;√6}

Vì −√6; √6 ∉ Z nên B = ∅.

Vậy tập hợp B là tập rỗng.

Bài 1.12 trang 19 SGK Toán 10 KNTT

Cho X = {a; b}. Các cách viết sau đúng hay sai? Giải thích kết luận đưa ra.

a) a ⊂ X;

b) {a} ⊂ X;

c) ∅ ∈ X.

Lời giải

Ta có a là phần tử thuộc tập X suy ra a thuộc tập X nên ta viết a ∈ X. Do đó phát biểu a) sai.

Ta có a là phần tử thuộc tập X suy ra {a} là tập con của tập X nên ta viết {a} ⊂ X. Do đó phát biểu b) là đúng.

∅ là kí hiêu của tập hợp rỗng và tập rỗng là con của tất cả các tập hợp khác nên ∅ ⊂ X Do đó phát biểu c) là sai.

Bài 1.13 trang 19 SGK Toán 10 KNTT

Cho A = {2; 5}, B = {5; x}, C = {2; y}. Tìm x, y để A = B = C.

Lời giải

Ta có A = {2; 5} và B = {5; x}

Để A = B thì x = 2.

Ta lại có A = {2; 5} và C = {2; y}

Để A = C thì y = 5.

Vậy x = 2, y = 5 thì A = B = C.

Bài 1.14 trang 19 SGK Toán 10 KNTT

Cho A = {x ∈ ℤ | x < 4};

B = {x ∈ ℤ | (5x – 3x2) ( x2 + 2x – 3) = 0}

a) Liệt kê các phần tử của hai tập hợp A và B.

b) Hãy các định các tập hợp A ∩ B, A ∪ B và A\B.

Lời giải

a) Tập hợp A gồm các số nguyên thỏa mãn nhỏ hơn 4. Do đó A = {…; -3; -2; -1; 0; 1; 2; 3}.

Ta có: (5x – 3x2) (x2 + 2x – 3) = 0

⇔\(\left\{\begin{array}{l}5x-3x^2=0\;\\x^2+2x-3=0\end{array}\right.\)

⇔\(\left\{\begin{array}{l}x\;=0\\x\;=\;\frac53\\x\;=\;1\\x\;=\;-3\end{array}\right.\)

Mà x ∈ ℤ nên x ∈ { -3; 0; 1}

Suy ra B = {-3; 0; 1}.

b) Ta có:

A ∩ B= {-3; 0; 1} = B;

A ∪ B = {…; -3; -2; -1; 0; 1; 2; 3} = A;

A\B = {…; -4; -2; -1; 2; 3}.

Bài 1.15 trang 19 SGK Toán 10 KNTT

Hãy xác định các tập hợp sau và biểu diễn chúng trên trục số.

a) ( –4; 1] ∩ [0;3);

b) (0;2] ∪ (–3;1];

c) (–2;1) ∩ (–∞;1];

d) ℝ \ (–∞;3].

Lời giải

Bài 1.16 trang 19 SGK Toán 10 KNTT

Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:

a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?

b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?

c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?

Lời giải

a) Ban tổ chức đã huy động số người phiên dịch cho hội nghị đó là:

35 + 30 – 16 = 49 (người)

Vậy ban tổ chức đã huy động 49 người phiên dịch cho hội nghị đó.

b) Số người chỉ phiên dịch được tiếng Anh là:

35 – 16 = 19 (người)

Vậy có 19 người chỉ phiên dịch được tiếng Anh.

c) Số người chỉ phiên dịch được tiếng Pháp là:

30 – 16 = 14 (người)

Vậy có 14 người chỉ phiên dịch được tiếng Pháp.

Giải Toán 10 Bài Tập hợp và các phép toán trên tập hợp sách Cánh Diều

Bài 1 trang 18 SGK Toán 10 CD Tập 1

Cho tập hợp X = {a; b; c}. Viết tất cả các tập con của tập hợp X.

Lời giải

Các tập hợp con của tập hợp X = {a; b; c} là:

X, {a}, {b}, {c}, {a; b}, {a; c}, {b; c}.

Bài 2 trang 18 SGK Toán 10 CD Tập 1

Sắp xếp các tập hợp sau theo quan hệ “⊂”: [2; 5], (2; 5), [2; 5), (1; 5]

Lời giải

Tập hợp [2; 5] là tập hợp gồm các số thực lớn hơn hoặc bằng 2 và nhỏ hơn hoặc bằng 5.

Tập hợp (2; 5) là tập hợp gồm các số thực lớn hơn 2 và nhỏ hơn 5.

Tập hợp [2; 5) là tập hợp gồm các số thực lớn hơn hoặc bằng 2 và nhỏ hơn 5.

Tập hợp (1; 5] là tập hợp các số thực lớn hơn 1 và nhỏ hơn hoặc bằng 5.

Do đó ta sắp xếp các tập hợp như sau:

(2; 5) ⊂ [2; 5) ⊂ [2; 5] ⊂ (1; 5].

Bài 3 trang 18 SGK Toán 10 CD Tập 1

Xác định các tập hợp sau và biểu diễn chúng trên trục số:

a) [– 3; 7] ∩ (2; 5);

b) (– ∞; 0] ∪ (– 1; 2);

c) R\ (– ∞; 3);

Lời giải

a) Do (2; 5) ⊂ [–3 ; 7] nên giao của hai tập hợp [–3; 7] và (2; 5) là khoảng (2; 5)

Vậy [– 3; 7] ∩ (2; 5) = (2; 5) và được biểu diễn là:

b) Ta có: (– ∞; 0] = {x ∈ R| x ≤ 0}

(–1 ; 2) = {x ∈ R| –1 < x < 2}

Khi đó (– ∞; 0] ∪ (–1 ; 2) = {x ∈ R| x ≤ 0 hoặc – 1 < x < 2} = {x ∈ R| x < 2} = (– ∞; 2)

Vậy (– ∞; 0] ∪ (– 1; 2) = (– ∞; 2) và được biểu diễn là:

c) Tập hợp ℝ\ (– ∞; 3) là tập hợp các số thực không thuộc khoảng (– ∞; 3)

Vậy ℝ\ (– ∞; 3) = [3; + ∞) và được biểu diễn là:

d) Tập hợp (– 3; 2) \ [1; 3) gồm các phần tử thuộc (– 3; 2) và không thuộc [1; 3).

Vậy (– 3; 2) \ [1; 3) = (– 3; 1) và được biểu diễn là:

Bài 4 trang 18 SGK Toán 10 CD Tập 1

Gọi A là tập nghiệm của phương trình x2 + x – 2 = 0, B là tập nghiệm của phương trình 2x2 + x – 6 = 0.

Tìm C = A ∩ B.

Lời giải

+ Giải phương trình x2 + x – 2 = 0

Ta có: ∆ = 12 – 4 . 1 . (– 2) = 1 + 8 = 9

Suy ra phương trình có hai nghiệm x1 = 1 và x2 = – 2.

Ta viết tập hợp A như sau: A = {–2 ; 1}.

+ Tương tự, giải phương trình 2x2 + x – 6 = 0 ta được 2 nghiệm là 3/2 và – 2.

Do đó ta viết được tập hợp B như sau: B = {– 2; 3/2}.

+ Ta có: C = A ∩ B hay tập hợp C là giao của hai tập hợp A và B, hay mọi phần tử thuộc tập hợp C phải vừa thuộc tập hợp A vừa thuộc tập hợp B.

Vậy C = {– 2}.

Bài 5 trang 18 SGK Toán 10 CD Tập 1

Tìm D = E ∩ G biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:

a) 2x + 3 ≥ 0 và – x + 5 ≥ 0;

b) x + 2 > 0 và 2x – 9 < 0.

Lời giải

Chú ý: D = E ∩ G hay tập hợp D là giao của hai tập hợp E và G. Ta cần tìm tập E, G bằng cách tìm tập nghiệm của các bất phương trình đã cho rồi từ đó suy ra tập hợp D.

a) 2x + 3 ≥ 0 và – x + 5 ≥ 0

Ta giải các bất phương trình.

2x + 3 ≥ 0 ⇔ x ≥ −3/2

Khi đó E = {x ∈ R∣ x ≥ −3/2} = [−3/2;+∞)

– x + 5 ≥ 0 ⇔ x ≤ 5

Khi đó G = {x ∈ ℝ| x ≤ 5} = (– ∞; 5]

Vậy D = E ∩ G = [−3/2;+∞) ∩ (−∞;5] = [−3/2;5]

b) x + 2 > 0 và 2x – 9 < 0

Ta có: x + 2 > 0 ⇔ x > – 2

Khi đó E = {x ∈ ℝ| x > – 2} = (– 2; + ∞)

Lại có: 2x – 9 < 0 ⇔ x < 9/2

Khi đó G = {x ∈ R∣ x < 9/2}

Vậy D = E ∩ G = (−2;+∞) ∩ (−∞;9/2) = (−2;9/2)

Bài 6 trang 18 SGK Toán 10 CD Tập 1

Gọi A là tập nghiệm của đa thức P(x). Viết tập hợp các số thực x sao cho biểu thức \(\frac1{P(x)}\) xác định.

Lời giải

A là tập nghiệm của đa thức P(x).

Suy ra A = {x ∈ℝ| P(x) = 0}.

Biểu thức  \(\frac1{P(x)}\)  xác định khi P(x) ≠ 0.

Do đó tập hợp các số thực x sao cho biểu thức  \(\frac1{P(x)}\)  xác định chính là tập hợp các số thực không thuộc A.

Gọi B là tập hợp các số thực x sao cho biểu thức  \(\frac1{P(x)}\)  xác định.

Vậy B = ℝ\A = CℝA.

Bài 7 trang 18 SGK Toán 10 CD Tập 1

Lớp 10B có 28 học sinh tham gia câu lạc bộ thể thao và 19 học sinh tham gia câu lạc bộ âm nhạc. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên.

a) Có bao nhiêu học sinh ở lớp 10B tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?

b) Có bao nhiêu học sinh ở lớp 10B tham gia ít nhất một trong hai câu lạc bộ trên?

c) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham giac câu lạc bộ thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ?

Lời giải

a) Có 10 bạn học sinh tham gia cả hai câu lạc bộ thể thao và âm nhạc, do đó trong 28 bạn học sinh tham gia câu lạc bộ thể thao của lớp 10B thì có 10 bạn tham gia cả câu lạc bộ âm nhạc.

Vậy số học sinh tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc của lớp 10B là: 28 – 10 = 18 (học sinh).

b) Số học sinh tham gia ít nhất một trong hai câu lạc bộ là:

28 + 19 – 10 = 37 (học sinh).

c) Lớp 10B có tất cả 40 học sinh, trong đó có 28 bạn tham gia câu lạc bộ thể thao, nên số học sinh không tham gia câu lạc bộ thể thao là:

40 – 28 = 12 (học sinh)

* Tính số học sinh không tham gia cả hai câu lạc bộ

TH1: Theo câu b, ta thấy có 37 học sinh tham gia ít nhất một trong hai câu lạc bộ nên số học sinh không tham gia cả hai câu lạc bộ (không tham gia bất kì câu lạc bộ nào) là:

40 – 37 = 3 (học sinh)

TH2: Học sinh không tham gia đồng thời cả hai câu lạc bộ thì số học sinh đó sẽ là:

40 – 10 = 30 (học sinh)

Bài 8 trang 18 SGK Toán 10 CD Tập 1

Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết 4 học sinh của nhóm không tham gia tiết mục nào?

Lời giải

Trong nhóm có 4 bạn không tham gia tiết mục nào nên số bạn trong nhóm tham gia hát hoặc múa là: 12 – 4 = 8 (bạn)

Trong 8 bạn trên, có 5 bạn học sinh tham gia múa, vậy số học sinh không tham gia tiết mục múa nhưng có tham gia tiết mục hát là: 8 – 5 = 3 (bạn)

Vì có 3 học sinh tham gia cả hai tiết mục, nghĩa là 3 bạn này thuộc trong nhóm 5 học sinh tham gia tiết mục múa, đồng thời khác với 3 bạn tham gia tiết mục hát nhưng không tham gia tiết mục múa.

Do vậy, số bạn trong nhóm tham gia tiết mục hát là: 3 + 3 = 6 (bạn)

Vậy có 6 học sinh tham gia tiết mục múa.

------------------------------------

Giải Toán 10 bài 3 sách giáo khoa cũ

A. Lí thuyết Các phép toán tập hợp

I. Giao của hai tập hợp

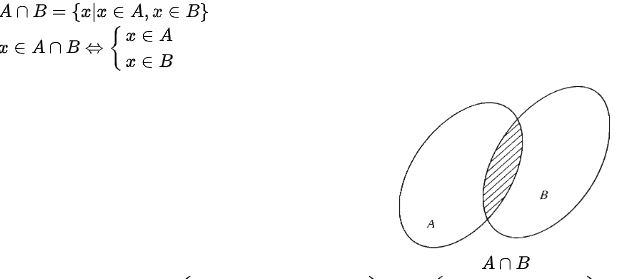
- Giao của hai tập hợp A và B, kí hiệu là A ∩ B là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B

Ví dụ: Cho tập hợp

a. Liệt kê các phần tử của A

b. Liệt kê các phần tử thuộc A ∩ B

Hướng dẫn

a. Các phần tử của tập

b. A ∩ B = {8}

II. Hợp của hai tập hợp

- Hợp của hai tập hợp A và B kí hiệu là A ∪ B là tập hợp gồm các phần tử thuộc A hoặc thuộc B

Ví dụ: Cho tập hợp

Hướng dẫn:

A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

III. Hiệu và phần bù của hai tập hợp

- Hiệu của tập hợp A và tập hợp B, kí hiệu là A\B tập hợp gồm các phần tử thuộc A không thuộc B.

Khi A ⊂ B thì A \ B gọi là phần bù của B trong A, kí hiệu là CAB

B. Giải SGK Toán 10 Bài 3

Trong Sách giáo khoa Toán lớp 10, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 10. Mời các bạn học sinh tham khảo:

• Giải bài tập SGK Toán lớp 10 (Đại số) chương 1: Các phép toán tập hợp

C. Giải SBT Toán 10 Bài 3

Sách bài tập Toán 10 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:

• Giải bài tập Toán 10 SBT bài 3 chương 1

D. Bài tập trắc nghiệm Toán 10 Các phép toán tập hợp

Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của phần Tập hợp này, VnDoc xin gửi tới các bạn học sinh Tài liệu Bài tập về Các phép toán tập hợp do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:

• Bài tập Toán 10 chương 1: Mệnh đề - Tập hợp
• Tập hợp và các phép toán tập hợp
• Bài tập Toán lớp 10 chương 1: Mệnh đề - Tập hợp

E. TÀI LIỆU HỌC TẬP SGK TOÁN 10 MỚI

• Toán 10 KNTT
• Toán 10 CTST
• Toán 10 CD

Trên đây VnDoc đã giới thiệu tới các bạn bài Toán 10 Bài 3: Các phép toán tập hợp. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Toán lớp 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!