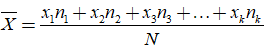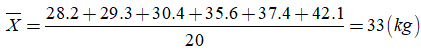Toán 7 | Bài 4: Số Trung Bình Cộng

A. Lý thuyết

1. Số trung bình cộng của dấu hiệu

Dựa vào bảng “tần số”, ta có thể tính số trung bình cộng của dấu hiệu (kí hiệu X−) như sau:

   + Nhân từng giá trị với tần số tương ứng.

   + Cộng tất cả các tích vừa tính được.

   + Chia tổng đó cho số các giá trị (tức là tổng các tần số).

   + Công thức tính:

Trong đó:

   • x1, x2,...., xn là k giá trị khác nhau của dấu hiệu X.

   • n1, n2,...., nk là k là tần số tương ứng.

   • N là số các giá trị

2. Ý nghĩa của số trung bình cộng

   + Số trung bình cộng thường được dùng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.

   + Khi các giá trị của dấu hiệu có khoảng chênh lệch rất lớn đối với nhau thì không nên lấy số trung bình cộng làm “đại diện” cho dấu hiệu đó.

   + Số trung bình cộng có thể không thuộc dãy giá trị của dấu hiệu.

3. Mốt của dấu hiệu

   + Mốt của dấu hiệu là giá trị tần số lớn nhất trong bảng “tần số”, kí hiệu là .

   + Có những dấu hiệu có hai mốt hoặc nhiều hơn

4. Ví dụ

Số cân nặng (làm tròn đến kg) của 20 học sinh được ghi lại như sau:

28	35	29	37	30	35	37	30	35	29
30	37	35	35	42	28	35	29	27	30

Ta có bảng “tần số”

Số cân (x)	28	29	30	35	37	42
Tần số (n)	2	3	4	6	4	1

Số trung bình cộng là:

Mốt của dấu hiệu: 35

B. Trắc nghiệm & Tự luận

Số cân của 45 học sinh lớp 7 được chọn một cách tùy ý trong số các học sinh lớp 7 của một trường THCS được cho trong bảng sau (tính tròn theo kg)

Số cân (x)	28	30	31	32	36	40	45
Tần số (n)	5	6	12	12	4	4	2	N = 45

(Áp dụng câu 1 và câu 2)

Bài 1: Số trung bình cộng là?

A. 32 kg            B. 32,7 kg            C. 32,5 kg            D. 33 kg

Lời giải:

Số trung bình cộng là:

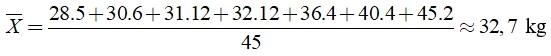
Chọn đáp án B.

Bài 2: Mốt là?

A. 31            B. 32            C. 28            D. Cả A và B đều đúng

Lời giải:

Mốt là số cân nặng của một học sinh có tần số lớn nhất

Số học sinh cân nặng 31 kg và 32 kg là nhiều nhất với tần số là 12.

Vậy mốt là 31 và 32

Chọn đáp án D.

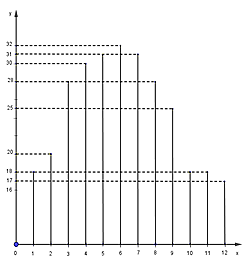
Cho biểu đồ nhiệt độ trung bình hàng tháng ở một địa phương trong vòng một năm với Ox là tháng, Oy là nhiệt độ trung bình (độ C)

(Áp dụng câu 3, câu 4 và câu 5)

Bài 3: Tháng nóng nhất là

A. Tháng 6            B. Tháng 7            C. Tháng 8            D. Tháng 9

Lời giải:

Từ biểu đồ đoạn thẳng ta thấy tháng 6 có nhiệt độ cao nhất là 32 độ.

Chọn đáp án A.

Bài 4: Tháng lạnh nhất là

 

A. Tháng 12            B. Tháng 11            C. Tháng 1            D. Tháng 2

Lời giải:

Từ biểu đồ đoạn thẳng ta thấy tháng 12 có nhiệt độ thấp nhất là 17 độ.

Chọn đáp án A.

Bài 5: Khoảng thời gian nóng nhất trong năm là

A. Từ tháng 10 đến tháng 12

B. Từ tháng 4 đến tháng 7

C. Từ tháng 1 đến tháng 3

D. Từ tháng 7 đến tháng 10

Lời giải:

Khoảng thời gian nóng nhất trong năm là: Từ tháng 4 đến tháng 7

Chọn đáp án B.

C.Bài tập tự luyện

Bài 1: Xạ thủ A và B thi bắn súng, mỗi người bắn 10 phát súng, kết quả điểm như sau:

A	5	7	10	8	9	7	8	10	5	8
B	7	8	6	6	7	5	6	7	6	6

Tính điểm trung bình của mỗi xạ thủ và cho biết ai bắn tốt hơn.

Bài 2: Điểm của Ban giám khảo cho thí sinh A và B như sau:

Thí sinh A	8	8,5	9	9	9	8
Thí sinh B	8	8	8,5	8,5	8	6

Tính điểm trung bình của mỗi thí sinh và cho biết ai bước tiếp vào vòng trong

Bài 3: Tính số trung bình cộng và tìm mốt của dãy giá trị sau bằng cách lập bảng:

17	20	18	18	19	17	22	30	18	21
17	32	19	20	26	18	21	24	29	21
28	18	19	31	26	26	31	24	24	22

Bài 4: Theo dõi nhiệt độ trung bình hàng năm của hai thành phố A và B từ năm 1956 đến năm 1975 (đo theo độ C) người ta lập được các bảng sau:

* Đối với thành phố A

Nhiệt độ trung bình (x)	23	24	25	26
Tần số (n)	5	12	2	1	N = 20

* Đối với thành phố B

Nhiệt độ trung bình (x)	23	24	25
Tần số (n)	7	10	3	N = 20

Hãy so sánh nhiệt độ trung bình hàng năm giữa hai thành phố

Bài 5: Hai xạ thủ A và B cùng bắn 20 phát đạn, kết quả ghi lại được dưới đây:

a. Tính điểm trung bình của từng xạ thủ

b. Có nhận xét gì về kết quả và khả năng của từng người.

Bài 6: Tổng số áo sơ mi mà một cửa hàng bán trong một ngày được thống kê lại trong bảng sau:

Cỡ áo	37	38	39	40	41
Số áo bán được	4	7	10	3	1

a) Số áo bán được là bao nhiêu?

b) Mốt của dấu hiệu là:

(A) 41;

(B) 10;

(C) 39;

(D) 25.

Hãy chọn phương án đúng.

Bài 7: Mật độ dân số của một số tỉnh, thành phố ở nước ta năm 2008 được cho trong bảng sau:

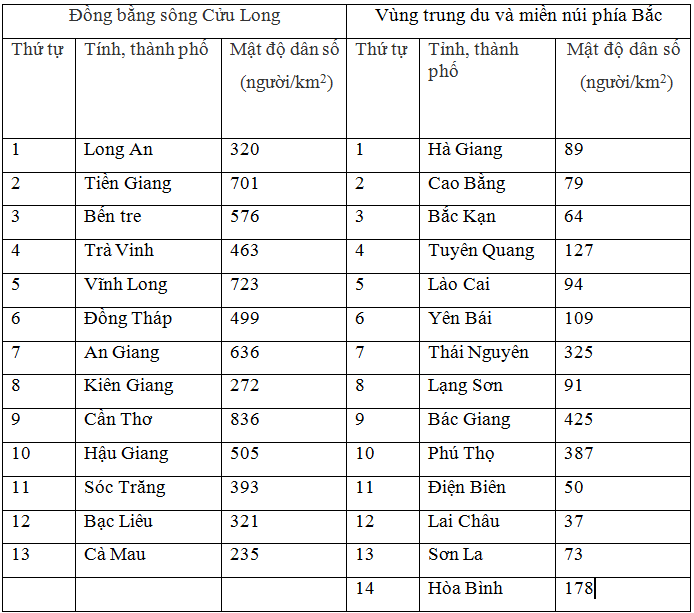
Mật độ dân số của một địa phương được tính bằng cách: Lấy tổng số dân trung bình của địa phương đó (tại một thời điểm nhất định) chia cho diện tích của chính địa phương ấy (người/km2).

a) Dấu hiệu ở đây là gì?

b) Nhận xét chung về mật độ dân số ở hai vùng

c) Tính mật độ dân số của từng vùng và so sánh.

D.Gợi ý đáp án

Bài 1:

Áp dụng công thức tính số trung bình cộng ta có:

Điểm trung bình của xạ thủ A là

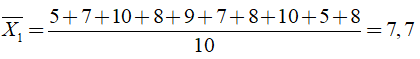
Điểm trung bình của xạ thủ B là

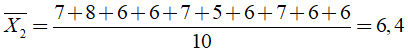
Do đó, A bắn tốt hơn vì A có điểm trung bình cao hơn.

Bài 2:

Áp dụng công thức tính trung bình cộng:

Điểm trung bình cộng của thí sinh A là:

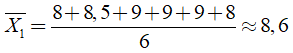
Điểm trung bình cộng của thí sinh B là:

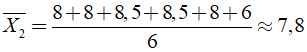
Do đó, A là thí sinh vào vòng trong vì điểm trung bình của thí sinh A cao hơn

Bài 3:

Giá trị (x)	Tần số (n)	Các tích (x.n)
17	3	51
18	5	90
19	4	76
20	2	40
21	3	63
22	2	44
24	3	72
26	3	78
28	1	28
30	1	30
31	2	62
32	1	32
	N = 30	Tổng: 666	X = 666/30 = 22,2

Mo = 18

Bài 4:

* Nhiệt độ trung bình của thành phố A

Giá trị (x)	Tần số (n)	Các tích (x.n)
23	5	115
24	12	288
25	2	50
26	1	26
	N = 20	Tổng: 479	X− = 479/20 = 23,95oC

*Nhiệt độ trung bình của thành phố B

Giá trị (x)	Tần số (n)	Các tích (x.n)
23	7	161
24	10	240
25	3	75
	N = 20	Tổng: 476	X−= 476/20 = 23,8oC

Nhiệt độ thành phố A nóng hơn nhiệt độ thành phố B

Bài 5:

* Điểm trung bình của xạ thủ A

Giá trị (x)	Tần số (n)	Các tích (x.n)
8	5	40
9	6	54
10	9	90
	N = 20	Tổng: 184	X−−− = 184/20 = 9,2

* Điểm trung bình của xạ thủ B

Giá trị (x)	Tần số (n)	Các tích (x.n)
6	2	12
7	1	7
9	5	45
10	12	120
	N = 20	Tổng: 184	X−−− = 184/20 = 9,2

Nhận xét: Điểm trung bình của hai xạ thủ như nhau nên khả năng như nhau.

Tuy nhiên nhìn kết quả có thể thấy xạ thủ A có phong độ ổn định hơn.

Bài 6:

a) 25 cái áo

b) (C)

Bài 7:

a) Mật độ dân số của một tỉnh

b) - Mật độ dân số vùng Đồng bằng sông Cửu Long nói chung cao hơn so so với vùng Trung du và miền núi phía Bắc.

- Mật độ dân số của vùng Trung du và miền núi phía Bắc: 152(người/km2). Rõ ràng là mật độ dân số ở đồng bằng sông cửu Long cao hơn vùng Trung du và miền núi phía Bắc.

Bài viết gợi ý:

1. QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC và ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC

2. Chuyên Đề Tam Giác - Hình Học 7

3. Hàm số

4. Tính chất của dãy số bằng nhau

5. Phương pháp chứng minh ba điểm thẳng hàng

6. Cộng trừ số hữu tỉ

7. Cộng trừ đa thức