[Toán 8] Định Lý Ơ-le | Cộng đồng Học Sinh Việt Nam - HOCMAI Forum

• Diễn đàn Bài viết mới Tìm kiếm trên diễn đàn
• Đăng bài nhanh
• Có gì mới? Bài viết mới New media New media comments Status mới Hoạt động mới
• Thư viện ảnh New media New comments Search media
• Story
• Thành viên Đang truy cập Đăng trạng thái mới Tìm kiếm status cá nhân

Đăng nhập Đăng ký

Tìm kiếm

Everywhere Đề tài thảo luận This forum This thread Chỉ tìm trong tiêu đề By: Search Tìm nâng cao… Everywhere Đề tài thảo luận This forum This thread Chỉ tìm trong tiêu đề By: Search Advanced…

• Bài viết mới
• Tìm kiếm trên diễn đàn

Menu Install the app Install [Toán 8] Định lý Ơ-le

• Thread starter nhatvy2606
• Ngày gửi 11 Tháng tư 2012
• Replies 2
• Views 23,688

• Bạn có 1 Tin nhắn và 1 Thông báo mới. [Xem hướng dẫn] để sử dụng diễn đàn tốt hơn trên điện thoại

• Diễn đàn
• TOÁN
• TRUNG HỌC CƠ SỞ & TIỂU HỌC
• Toán lớp 8
• Hình học

You are using an out of date browser. It may not display this or other websites correctly.You should upgrade or use an alternative browser. N

nhatvy2606

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Chứng minh định lý Ơ-le bằng các kiến thức đã học ở lớp 8. 6

654321sss

http://forum.mathscope.org/showthread.php?t=1805 đó là link tham khảo. có gì bạn tải tệp về mà tự hoc nhá còn cách lớp 8 nè : Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) . Chứng minh H , G , O thẳng hàng ? Giải : Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O)) Xét tứ giác BHCD ta có : BH // DC ( vì cùng vuông góc với AC ) CH // DB ( vì cùng vuông góc với AB ) Do đó tứ giác BHCD là hình bình hành . ===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành) Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1) GI = 1/2 GA (t/chất trọng tâm của ABC ) (2) góc HAG = góc GIO ( so le trong vì AH // OI ) (3) Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c) ===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng ) Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng . N

nguyenlamlll

Chứng minh đường thẳng Euler, đường tròn Euler, và định lý Euler Mình sẽ giúp bạn chứng minh lần lượt cả 3 cái luôn: Đường thẳng, Đường tròn, Định lý. Nhiều hơn cũng không sao ha ^^!, bạn tham khảo: 1. Chứng minh đường thẳng Euler Cách 1: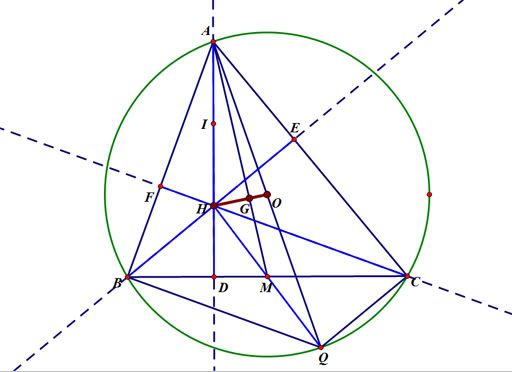 Vẽ [tex]\large\Delta[/tex]ABC có giao điểm ba đường cao AD, BE, CF là H. G là trọng tâm của [tex]\Delta[/tex]ABC. Từ B vẽ đường thẳng song song với HC, từ C vẽ đường thẳng song song với HB, chúng cắt nhau tại Q. Gọi M là giao điểm của HQ và BC. Xét tứ giác HCQB ta có : [tex]\{ \begin BH// CQ (gt) \\BQ//CH (gt)[/tex] \Rightarrow Tứ giác HCQB là hình bình hành vì có 2 cặp cạnh đối song song \Rightarrow MB = MC và MH = MQ (tính chất đường chéo hình bình hành) Xét [tex]\Delta[/tex]ABC có AM là đường trung tuyến (MB=MC): Mà G là trọng tâm [tex]\Delta[/tex]ABC (gt) \Rightarrow[tex]MG=\frac{1}{3}AM[/tex] Xét [tex]\Delta[/tex]AHQ có AM là đường trung tuyến (MH=MQ) Mà [tex]MG=\frac{1}{3}AM[/tex] (cmt) \Rightarrow G là trọng tâm [tex]\Delta[/tex]AHQ Ta có HO là đường trung tuyến (OA=OQ=R) \RightarrowG [tex]\in\[/tex] HO. ====== Mình không rõ lớp 8 học đường tròn chưa, nên các kiến thức như góc nội tiếp chắn nửa đường tròn là góc vuông thì chắc là bạn chưa biết (nếu bạn học lớp 8) . Cách chứng minh thì như trên. Không chứng minh song song được thì đành tự vẽ ra thôi ^^! ====== Cách 2: CM: HCQB là hình bình hành CM: [tex]\frac{AG}{MG} =2 = \frac{AH}{OM}[/tex] bằng tính chất đường trung bình trong [tex]\Delta[/tex]AHQ và tính chất trọng tâm trong [tex]\Delta[/tex]ABC CM: [tex]\Delta[/tex]AHG và [tex]\Delta[/tex]MOG đồng dạng \Rightarrow [tex]\widehat{AGH}=\widehat{MGO}[/tex] (1) Ta có: [tex]\widehat{HGA} + \widehat{HGM} = 180^0 [/tex](2 góc kề bù) (2) Từ (1) & (2) ta có: [tex]\widehat{MGO} + \widehat{HGM} = 180^0 [/tex] \Rightarrow H, G, O thẳng hàng. 2. Chứng minh đường tròn Euler Gọi K là trung điểm của OH Cách 1: Gọi I là trung điểm của AH Xét [tex]\Delta[/tex]AHO có: [tex]\{ \begin IA=IH (gt) \\KH=KO (gt)[/tex] \Rightarrow IK là đường trung bình của [tex]\Delta[/tex]AHO \Rightarrow IK//AO; [tex]IK=\frac{1}{2}AO=\frac{R}{2}[/tex] (1) Cm tương tự: KM là đường trung bình của [tex]\Delta[/tex]HOQ \Rightarrow KM//OQ; [tex]KM=\frac{1}{2}OQ=\frac{R}{2}[/tex] (2) Từ (1), (2) \Rightarrow [tex]\{ \begin KI=KM=\frac{R}{2} \\I, K, M [/tex]thẳng hàng Xét [tex]\Delta[/tex]IDM vuông tại D có DK là trung tuyến (KI=KM) \Rightarrow[tex]KI=KM=DK=\frac{R}{2}[/tex] \RightarrowI, D, M [tex]\in\[/tex] [tex](K;\frac{R}{2})[/tex] Cm tương tự: 2 chân đường cao vẽ từ B và C, 2 chân đường trung tuyến vẽ từ B và C, 2 trung điểm HB và HC [tex]\ \in\ (K;\frac{R}{2})[/tex] Cách 2: Cập nhật sớm ^^! 3. Chứng minh định lý Euler Cập nhật sớm ^^! Last edited by a moderator: 14 Tháng tư 2012 You must log in or register to reply here. Chia sẻ: Facebook Reddit Pinterest Tumblr WhatsApp Email Chia sẻ Link

• Diễn đàn
• TOÁN
• TRUNG HỌC CƠ SỞ & TIỂU HỌC
• Toán lớp 8
• Hình học

Top Bottom

• Vui lòng cài đặt tỷ lệ % hiển thị từ 85-90% ở trình duyệt trên máy tính để sử dụng diễn đàn được tốt hơn.