Tổng Hợp Lý Thuyết Chuẩn Nhất Về Hệ Trục Tọa độ - Toán Lớp 10
Có thể bạn quan tâm
Ở trong bài biết này, Cunghocvui gửi đến bạn học kiến thức lý thuyết chính xác nhất về hệ trục tọa độ như trục tung trục hoành (hoành độ) trong mặt phẳng tọa độ, phương pháp tọa độ trong không gian, phương pháp tọa độ trong mặt phẳng, hệ trục tọa độ oxyz (hay hệ tọa độ trong không gian).
I) HỆ TRỤC TỌA ĐỘ
1) Định nghĩa
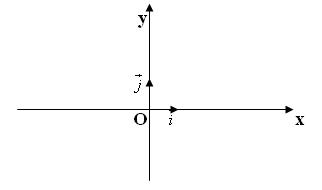
- Hệ trục tọa độ Oxy gồm hai trục hoành và trục tung vuông góc với nhau.
Trong đó
- O: gốc tọa độ
- Ox: trục hoành (hay hoành độ)
- Oy: trục tung (hay tụng độ)
- Đường thẳng mà trên đó đã xác định một điểm gốc O và một vecto đơn vị thì được gọi là trục tọa độ.
2) Nhận xét
\(\underset{a}{\rightarrow}= (x;y)= \underset{b}{\rightarrow}= (x'; y')\Leftrightarrow \left\{\begin{matrix}x=x' & \\ y=y' & \end{matrix}\right.\)
3) Các biểu thức tọa độ của vecto
Cho hai vecto: \(\underset{a}{\rightarrow}=(x;y)\), \(\underset{b}{\rightarrow}=(x';y')\). Ta có:
- \(\underset{a}{\rightarrow} + \underset{b}{\rightarrow} = (x+x'; y+y')\); \(\underset{a}{\rightarrow} - \underset{b}{\rightarrow} = (x-x'; y-y')\)
- \(k.\underset{a}{\rightarrow}= (kx; ky) \forall k\in \mathbb{R}\)
- \(\underset{b}{\rightarrow}\) cùng phương với \(\underset{a}{\rightarrow}\) khi và chỉ khi có số k, sao cho \(x' =kx, y' = ky\)
4) Một số phương pháp tọa độ trong mặt phẳng tọa độ oxy
a) Vecto chỉ phương (VTCP) của đường thẳng
\(\underset{u}{\rightarrow} = (u_1; u_2)\) là VTCP của đường thẳng \(\Delta\) thì:
- \(u \neq 0\)
- \(\underset{u}{\rightarrow} // (\equiv) \Delta\) (song song hoặc trùng)
- \(k.\underset{u}{\rightarrow} (k\neq 0)\) là VTPT của \(\Delta\)
b) Vecto pháp tuyến (VTPT) của đường thẳng:
\(\underset{n}{\rightarrow} (n_1; n_2)\) là VTPT của \(\Delta\) thì:
- \(\underset{n}{\rightarrow}\neq \underset{0}{\rightarrow}\)
- \(\underset{n}{\rightarrow}\) có giá vuông góc với \(\Delta\)
- \(k.\underset{n}{\rightarrow} (k\neq 0)\) là VTPT của \(\Delta\)
c) Phương trình đường thẳng
- Phương trình tổng quát: \(\Delta: Ax + By + C = 0 (A^2 + B^2 \neq 0)\)
- Phương trình tham số: qua điểm \(M(x_0; y_0)\) có VTCP \(\underset{u}{\rightarrow} = (u_1; u_2)\) có dạng:
\(\Delta: \left\{\begin{matrix}x=x_0+u_1 & \\ y=y_0+u_2 & \end{matrix}\right.\) (với \(u_1^2 + u_2^2 \neq0, t \in R\))
- Phương trình chính tắc: qua \(M(x_0; y_0), \) VTCP \(\underset{u}{\rightarrow} = (u_1; u_2)\) có dạng:
\(\dfrac {x-x_0}{u_1}= \dfrac {y-y_0}{u_2} (u_1 \neq 0, u_2\neq 0)\)
♦ Lưu ý: \(u_1, u_2 = 0\) thì phương trình không có phương trình chính tắc
II) HỆ TRỤC TỌA ĐỘ Oxyz
1) Định nghĩa
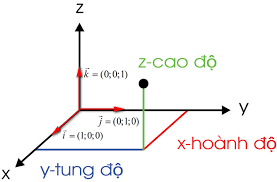
Hệ trục mà gồm có 3 trục Ox, Oy, Oz đôi một vuông góc với nhau thì được gọi là hệ trục tọa độ oxyz
Trong đó
- Ox là trục hoành (hay hoành độ)
- Oy là trục tung (hay tung độ)
- Oz là trục cao (hay cao độ)
2) Tọa độ điểm

Cho điểm M nằm trong hệ trục tọa độ oxyz, tọa độ của điểm M là (a; b; c)
- Với điểm M nằm trên các trục tọa độ
- \(M \in Ox => M (a; 0; 0)\)
- \(M \in Oy => M (0; b; 0)\)
- \(M \in Oz => M (0; 0; c)\)
- Với điểm M nằm trên mặt phẳng tọa độ
- M nằm trên Oxy thì M (a; b; 0)
- M nằm trên Oyz thì M (0; b; c)
- M nằm trên Oxz thì M (a; 0; c)
3) Một số phương pháp tọa độ trong không gian
- Tọa độ của điểm: \(\underset{OM}{\rightarrow}=x.\underset{i}{\rightarrow} + y.\underset{j}{\rightarrow} + z.\underset{k}{\rightarrow} \Leftrightarrow M(x; y; z)\)
- Tọa độ của vecto: \(\underset{a}{\rightarrow}=a_1.\underset{i}{\rightarrow} + a_2.\underset{j}{\rightarrow} + a_3.\underset{k}{\rightarrow} \Leftrightarrow \underset{a}{\rightarrow} = (a_1; a_2; a_3)\)
- Tính chất
Cho \(\underset{a}{\rightarrow} = (x_1; y_1; z_1), \underset{b}{\rightarrow} = (x_2; y_2; z_2)\) với số k bất kì thì ta có:
- Tổng 2 vecto là 1 vecto: \(\underset{a}{\rightarrow} + \underset{b}{\rightarrow} = (x_1 + x_2; y_1+y_2; z_1 + z_2)\)
- Hiệu 2 vecto là 1 vecto: \(\underset{a}{\rightarrow} - \underset{b}{\rightarrow} = (x_1 -x_2; y_1-y_2; z_1 - z_2)\)
- Tích của vecto với một số thực là 1 vecto: \(k.\underset{a}{\rightarrow}= k.(x_1; y_1; z_1) = (kx_1; ky_1;kz_1)\)
- Độ dài vecto: \(\left | \underset{a}{\rightarrow} \right | = \sqrt{x_1^2+y_1^2+z_1^2}\)
- Vecto không: \(\underset{0}{\rightarrow} = (0; 0; 0)\)
- Hai vecto bằng nhau thì tọa độ tương ứng bằng nhau
- Tích vô hướng: \(\underset{a}{\rightarrow}.\underset{b}{\rightarrow} = x_1.x_2 + y_1.y_2+z_1.z_2\)
- Góc giữa hai vecto: \(cos (\underset{a}{\rightarrow}.\underset{b}{\rightarrow} )= \dfrac {\underset{a}{\rightarrow}.\underset{b}{\rightarrow}}{\left | \underset{a}{\rightarrow} \right |.\left | \underset{b}{\rightarrow} \right |} = \dfrac {x_1.x_2+y_1.y_2+z_1.z_2}{\sqrt{x_1^2+y_1^2+z_1^2}\sqrt{x_2^2+y_2^2+z_2^2}}\)
Xem thêm >>> Hướng dẫn giải bài tập SGK
Trên đây là những kiến thức lý thuyết và phương pháp tọa độ trong không gian, phương pháp tọa độ trong mặt phẳng mà bạn cần nắm được mà Cunghocvui đã tổng hợp được. Hy vọng bài viết có thể giúp ích được nhiều cho bạn trong quá trình học tập, chúc bạn học tập tốt
Từ khóa » Trục Tọa độ Và Hệ Trục Tọa độ Nâng Cao
-
Bài 5. Trục Tọa độ Và Hệ Trục Tọa độ
-
Giải Toán 10 Nâng Cao Bài 5: Trục Tọa độ Và Hệ Trục Tọa độ
-
Trục Tọa độ Và Hệ Trục Tọa độ - Chuyên đề Hình Học 10
-
TOÁN LỚP 10-HÌNH NÂNG CAO-TRỤC TỌA ĐỘ VÀ HỆ ... - YouTube
-
Bài 5. Trục Tọa độ Và Hệ Trục Tọa độ
-
Bài 5: Trục Tọa độ Và Hệ Trục Tọa độ
-
16.2. Hệ Trục Tọa độ (hanthihnue@).html
-
Hệ Trục Tọa độ Lớp 10 Nâng Cao - 123doc
-
Giáo án Hình Học 10 Nâng Cao Tiết 10, 11: Trục Tọa độ Và Hệ Trục Tọa độ
-
Giải Toán 10 SGK Nâng Cao Chương 1 Bài 5 Trục Tọa độ Và Hệ Trục ...
-
Giải Toán 10 Nâng Cao: Bài 5. Trục Tọa độ Và Hệ Trục Tọa độ
-
Giáo án Hình Học Lớp 10 Nâng Cao - Tiết 10-11-12 Bài 5: Trục Toạ ...
-
Hình Học 10 Bài 4: Hệ Trục Tọa độ - MarvelVietnam
-
Trong Mặt Phẳng Tọa độ, Mỗi Mệnh đề Sau đúng Hay Sai ?. Bài 29 ...