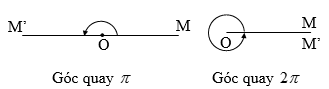Tổng Hợp Lý Thuyết Về Phép Quay - Có Thể Bạn Chưa Biết?

Bài viết dưới đây cunghocvui.com sẽ tổng hợp lý thuyết về chủ đề phép quay: từ công thức phép quay cho đến bài tập dạng tìm ảnh của đường thẳng qua phép quay...

I. Lý thuyết

1. Định nghĩa 

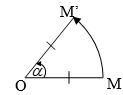
- Cho điểm O và góc lượng giác \(\alpha \) , phép biến hình biến O thành chính nó, biến mỗi điểm M thành M' sao cho OM' = OM và góc lượng giác (OM; OM') = \(\alpha \) được gọi là phép quay tâm O góc \(\alpha \).

Ký hiệu: \(Q_({O;\alpha })\).

 *Nhận xét: 

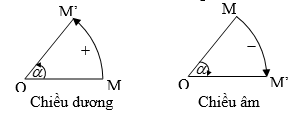
- Chiều dương của phép quay là chiều dương của đường tròn lượng giác, ngược lại là chiều âm. 

- Với số nguyên k:

+ Phép quay \(Q_{(O; k2\pi )}\) là phép đồng nhất. 

+ Phép quay \(Q_{(O; \pi + k2\pi )}\) là phép đối xứng tâm. 

2. Tính chất 

Phép quay là một phép dời hình nên có đầy đủ tính chất phép dời hình. 

a) Tính chất 1 

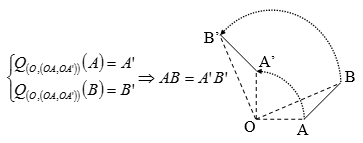
Phép quay bảo toàn khoảng cách giữa hai điểm bất kỳ. 

b) Tính chất 2

Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính. 

c) Nhận xét 

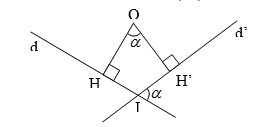
Phép quay góc quay \(O < \alpha < \pi \) biến đường thẳng d thành đường thẳng d' sao cho: 

+ (d, d') = \(\alpha\) nếu \(O < \alpha \leq \frac{\pi }{2}\)

+ (d, d') = \(\pi - \alpha\) nếu \( \frac{\pi }{2} \leq \alpha < pi\)

3. Biểu thức tọa độ phép quay 

Trong mặt phẳng tọa độ Oxy cho điểm M(x; y) và góc lượng giác \(\alpha\)

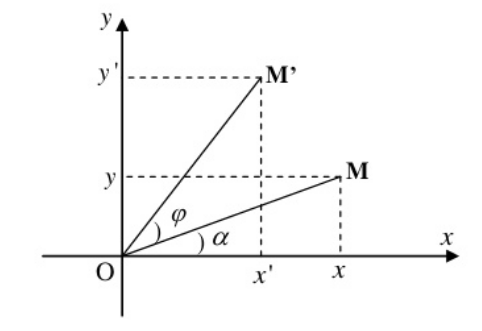
Gọi điểm M(x; y). Đặt OM = r và góc lượng giác (Ox; OM) = \(\alpha\).

Ta có: M\(\left\{\begin{matrix}x = rcos\alpha & \\ y = rcos\alpha & \end{matrix}\right.\)

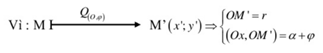
Tọa độ M'(x'; y'): \(\left\{\begin{matrix}x' = rcos(\alpha + \varphi) & \\ y' = rsin(\alpha + \varphi) & \end{matrix}\right.\)

Xem thêm: Phép dời hình và phép đồng dạng trong mặt phẳng

II. Bài tập phép quay có lời giải

1. Cho M (3; 4). Tìm ảnh của điểm M qua phép quay tâm O góc quay \(30^0\). 

Gọi M' (x'; y') = \(Q_{(O; 30^0)}\) .

Áp dụng biểu thức tọa độ của phép quay ta có:

\(\left\{\begin{matrix}x' = xcos\alpha - ysin\alpha & \\ y' = xsin\alpha + ycos\alpha & \end{matrix}\right.\)

Ta có: 

\(\left\{\begin{matrix}x' = 3cos30^o - 4sin30^o = \frac{3\sqrt{3}}{2} - 2 & \\ y' = 3sin30^0 + 4cos30^0 = \frac{3}{2} + 2\sqrt{3} & \end{matrix}\right.\)

=> M' (\( \frac{3\sqrt{3}}{2} - 2; \frac{3}{2} + 2\sqrt{3}\))

2. Cho hình vuông ABCD tâm O, M là trung điểm AB, N là trung điểm OA. Tìm ảnh của tam giác AMN qua phép tâm O góc quay \(90^0\). 

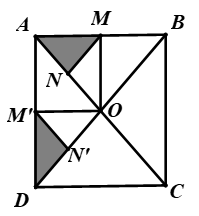
Phép quay \(Q_{(O; 90^0)}\) biến A thành D, biến M thành M' là trung điểm của AD, biến N thành N' là trung diểm của OD. 

Do đó biến tam giác AMN thành tam giác DM'N'. 

Trên đây là toàn bộ lý thuyết về chủ đề phép quay, rất mong bổ ích đối với độc giả. 

 

 

Tags phép quay toán lớp 11 công thức phép quay