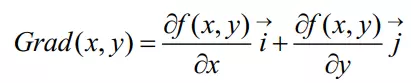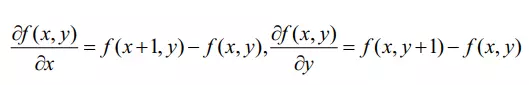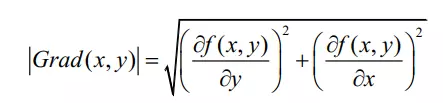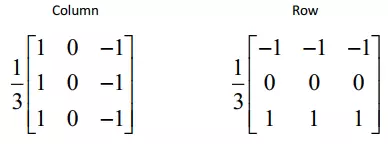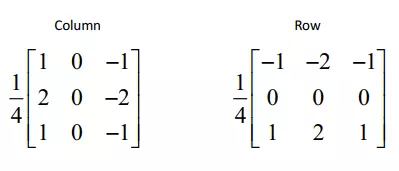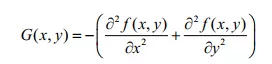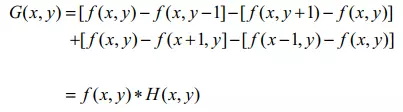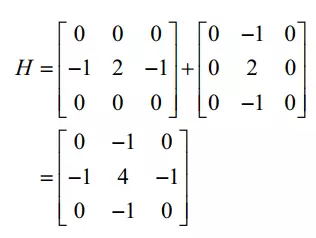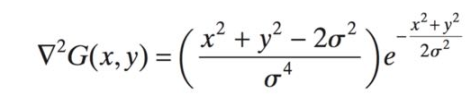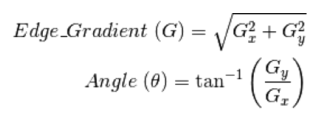Tuần 5: Gradient And Edge. - Viblo

Trong tuần này, mình sẽ giới thiệu về thuật toán tìm cạnh trong xử lý ảnh.

What is an edge ?

Trong ảnh số, những điểm ảnh có cường độ ảnh sáng thay đổi mạnh so với các điểm xung quanh thường được gọi là các điểm cạnh (edge point). Cạnh (edge) là tập hợp các điểm cạnh tạo nên một hình dạng có ý nghĩa nào đó liên quan đến thông tin hình dạng và cấu trúc của đối tượng trong ảnh, ví dụ đường bao của một khuôn mặt, cấu trúc vành mũ, ... Tách cạnh là quá trình trích rút các thông tin tin cạnh bằng các phép toán xử lý ảnh.

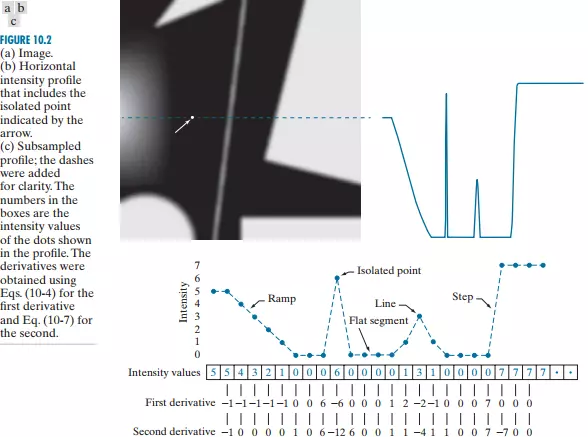
Ví dụ như ta có một bức ảnh và ta lấy một đường kẻ ngang rồi ta sẽ lấy mức xác theo đường thằng đó, ta sẽ thấy được sự thay đổi mức xám ở các ví trị.

Gradient

Khi nhắc đến sự thay đổi đổi thì ta thường nhắc tới Gradient. Gradient của hàm cho biết hàm tăng mạnh như thế nào.

• Ví dụ với hàm 1 chiều: f(x)=x2f(x) = x^{2}f(x)=x2 thì Gradient của nó được ký hiệu và tính như sau: Grad(x)=∂f(x)∂(x)=2xGrad(x) = \frac{\partial f(x)}{\partial (x)} = 2xGrad(x)=∂(x)∂f(x)​=2x
  • Grad (2) = 4 chỉ ra hướng tăng của hàm là bên phải
  • Grad (-1) = - 2 chỉ ra hướng tăng của hàm nằm ở bên trái.

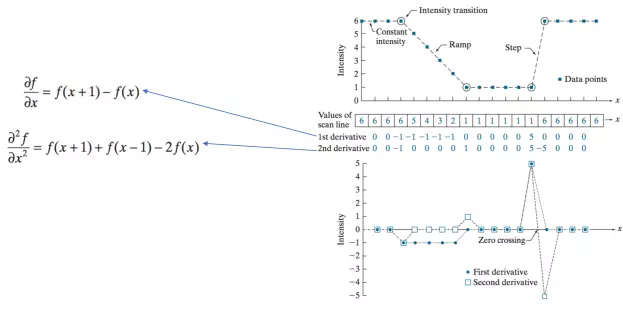
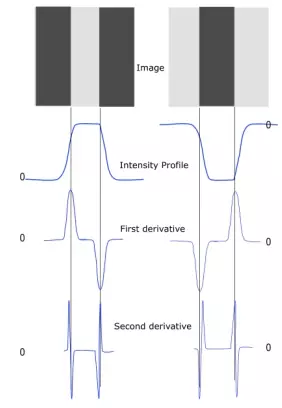
Gradient không chỉ tính bằng đạo hàm bậc 1, ta cũng thể tính bằng đạo hàm bậc. Với độ biến đổi của mức sáng bên trên ta tính được đạo hàm bậc 1, bậc 2 và công thức tương ứng như sau:

Edge detection using derivatives

Ta có 2 cách để phát hiện cạnh sử dụng đạo hàm là:

• Phát hiện giá trị cực tiểu hoặc cực đại địa phương trong đạo hàm bậc 1
• Phát hiện zero-crosssing (chính là chỗ giá trị từ âm sang dương hoặc ngược lại bạn có thể nhìn chú thích ở hình trên) trong đạo hàm bậc 2.

Đạo hàm trong không gian 2 chiều được tính như sau:

Tuy nhiên để áp dụng cho ảnh số, việc xấp xỉ hóa đạo hàm của hàm rời rạc là cần thiết. Xấp xỉ đạo hàm bậc nhất hàm gradient được tính như sau (1), ở đây giá trị nhỏ nhất trong ảnh là 1 pixel:

Độ lớn của Gradient cho biết cường đọi của cạnh tại điểm (x,y)(x,y)(x,y):

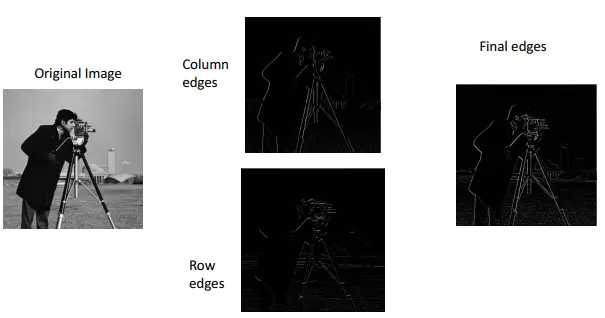
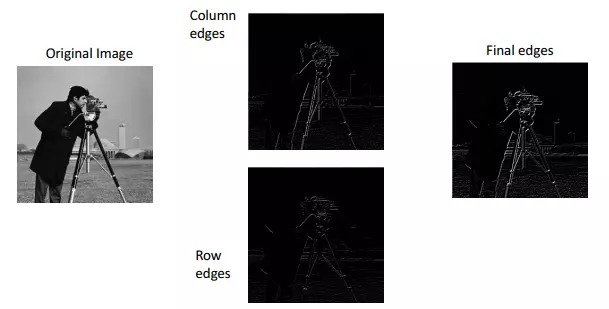
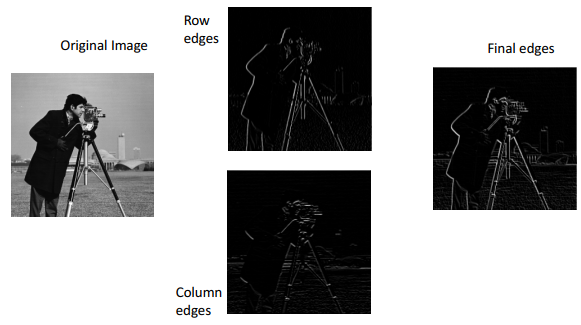
Trong ảnh số, ta có các bước để tính gradient như sau:

• Tính Gradient theo cột
• Tình Gradient theo hàng
• Tính Gradient cuối cùng bằng cách tổng hợp 2 Gradient bên trên.

Nếu ta tính gradient bằng phương pháp thông thường theo kiểu duyệt theo hàng và cột rồi tính thì rất mất thời gian, có cách nào làm nhanh hơn không ? Và ta có cách dùng phép toán sử dụng kernel ta học ở bài trước để tính toán.

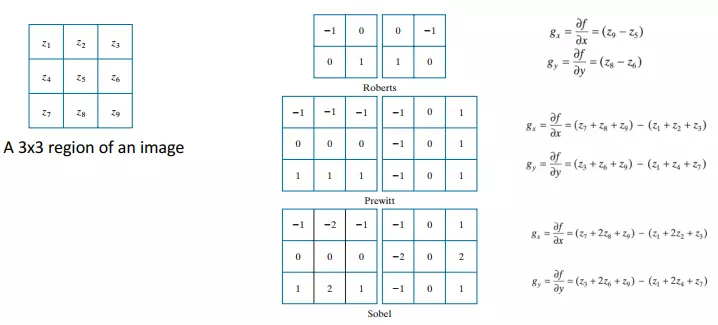
Various kernels used to compute the gradient

Ở đây, mình sẽ giới thiệu cho các bạn những kernel được sử dụng rộng rãi nhất trong xử lý ảnh. Đầu tiền ta có cái nhìn tổng quan về các kernel được giới thiệu như sau:

Pixel Difference masks

Kernel này thể hiện rõ công thức đạo hàm bậc 1 theo x và theo y bên trên (1) với -1 đằng sau số 1 vì ở đây ta thực hiện phép toán Convolution nên nó đảo ngược .

Ví dụ của một ảnh sử dụng kernel trên như sau:

Kết quả cho ra không được tốt cho lắm, vì thế ta sẽ tìm các hiểu tìm hiểu các kernel khác cho kết quả tốt hơn.

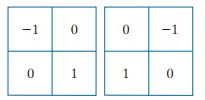
Robert mask

Roberts masks tính gradient theo đường chéo giữa 2 điểm. Kernel đạo hàm theo x và y như sau:

Kết quả với cùng một ảnh gốc ở ví dụ pixel difference masks với Robert mask như sau:

Ta thấy kết quả sẽ đậm hơn theo đường chéo mà không phải ngang hay dọc như ở kernel trước, Kernel kích thước 2 x 2 thường khó để cài đặt bởi tính toán của chính không rõ ràng. Do đó, cửa sổ kích thước 3 x 3 thường được sử dụng.

Prewitt mask

Prewitt mask được định nghĩa như sau:

Ta có một ví dụ sử dụng Prewitt mask.

Sobel mask

Một biến thể khác của Prewitt mask sử dụng tăng trọng số của điểm trung tâm lên 2 là Sobel mask. Giá trị 2 được sử dụng để làm mượt ảnh và cũng để đánh giá điểm trung tâm quan trọng hơn các điểm khác.

Và đây là kết quả khi sử dụng Sobel mask với bức ảnh đầu vào:

Laplace gradient

Các kernel ở trên đều tính gradient dựa trên đạo hàm bậc 1, với gradient đạo hàm bậc 2 theo cả hai chiều hay còn gọi là Laplace trong miền liên tục được nghĩa như sau:

Trong miền liên tục, công thức trên được xấp xỉ thành:

Ta có Laplace mask hay đại diện cho hàm H bên trên được nghĩa là:

Kết quả khi sử dụng Laplace mask khi sử dụng Laplace mask:

Ta thấy kết quả đẹp hơn nhiều ở ví trị đầu,... nhưng vẫn chưa tốt vì còn lấy các giá trị ở phần nền cỏ tạo ra các chấm rời rạc vì nhiệm vụ của tách cạnh là lấy ra những cạnh liền mạch có giá trị.

Ta có cái nhìn tổng quan khi áp dụng 5 kernel khác nhau để tách cạnh như sau:

More advanced edge detection

Laplacian of a Gaussian (LoG) edge detection

Không như các thuật toán trước tính gradient sử dụng các phép toán tuyến tính, thuật toán này tính theo hàm gaussian. Các bước thực hiện thuật toán như sau:

1. Áp dụng LoG cho ảnh:

2. Phát hiện những cũng zero-crossing trong ảnh.

3. Lọc ngưỡng trên zero-crossing chỉ để lại những điểm mạnh ( khác biệt lớn giữa cực đại dương và cực tiểu âm)

Ví dụ về các bước thực hiện của LoG edge như sau:

Canny edge detection

Phương pháp tách cạnh Canny sử dụng thuật toán có nhiều bước để tìm cạnh trong ảnh. Nó được phát triển bởi John F. Canny vào năm 1986. Hoạt động của phương pháp này có thể tóm tắt như sau:

1. Giảm nhiễu: Ảnh thu nhận được từ thiết bị thu nhận thường có nhiều nhiễu, để nhiễu không ảnh hướng đến quá trình tách cạnh nó cần được giảm thiểu. Làm mờ ảnh, giảm nhiễu dùng bộ lọc Gaussian kích thước 5x5. Kích thước 5x5 thường hoạt động tốt cho giải thuật Canny. Dĩ nhiên bạn cũng có thể thay đổi kích thước của bộ lọc làm mờ cho phù hợp.

2. Tính Gradient và hướng gradient: Tính Gradient cho mõi điểm ảnh sử dụng bộ lọc cạnh Sobel được giới thiệu ở trên. Sau đó xác định độ lớn của cạnh được định nghĩa là độ lớn của Gradient và hướng của cạnh là hướng của Gradient.

3. Non-maximum Suppression (viết tắt NMS): loại bỏ các pixel ở vị trí không phải cực đại toàn cục. Các điểm cạnh được định nghĩa là cực đại địa phương trogn ảnh độ lớn cạnh. Thuật toán để xác định điểm cạnh tại mỗi vị trí (x,y) được thực hiện như sau:

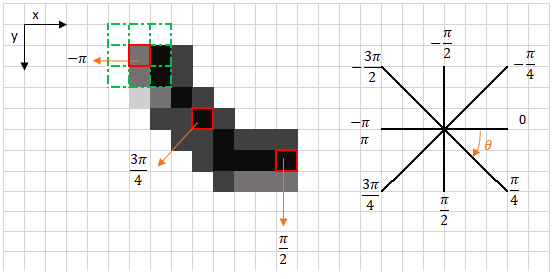
   • Làm tròn hướng cạnh Angle(θ)Angle(\theta)Angle(θ) tới góc là bội của 45∘45^{\circ}45∘ gần nhất tương ứng chỉ tới 8 điểm lân cận.
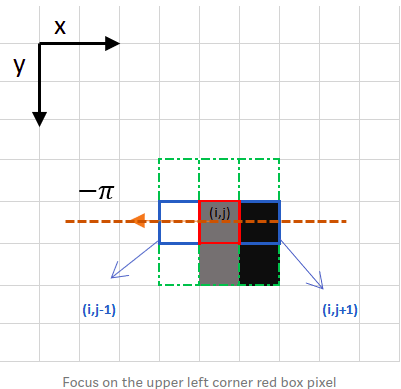
   • So sánh độ lớn cạnh của điểm (x,y) hiện tại với điểm lân cận theo hướng của cạnh và hướng ngược lại . Ví dụ nếu có Angle(θ)=−180∘Angle(\theta) = -180^{\circ}Angle(θ)=−180∘ thì 2 điểm lân cận phía sau và phía trước của điểm hiện tại được so sánh. Nếu độ lớn của cạnh của điểm (x,y) là lớn nhất thì điểm đó là cạnh, ngược lại thì không phải là cạnh.

4. Lọc ngưỡng: Các điểm cạnh được lựa chọn trong bước 3 hầu hết là những cạnh thực, tuy nhiên vẫn còn những điểm cạnh bị chọn sai vì nhiễu hoặc do biến đổi màu sắc trên bề mặt của một đối tượng. Cách đơn giản nhất để phan biệt chúng là sử dụng một ngưỡng mà chỉ những điểm cạnh nào có độ lớn lớn hơn ngưỡng này thì được giữ lại. Thuật toán tách cạnh Canny sử dụng ngưỡng kép bao gồm một ngưỡng cao và một ngưỡng thấp. Những điểm nào có độ lớn cạnh lớn hơn ngưỡng cao được đánh dấu là cạnh mạnh (strong edge). Những điểm nào nào có độ lớn năm giữa hai ngưỡng được đánh đấu là cạnh yếu (weak edge).

5. Cuối cùng: Các điểm được đánh dấu là cạnh mạnh được lựa chọn ngay là điểm cạnh. Những điểm cạnh yếu được chọn là điểm cạnh khi và chỉ khi nó nằm cạnh một điểm cạnh mạnh. Ở đây các điểm cạnh mạnh được coi là cạnh thực, những điểm cạnh yếu thì có thể là cạnh thực hoặc nhiễu. Và chúng chỉ có thể là cạnh thực nếu liền kề với một điểm là cạnh thực.

Trong opencv, ta muốn sử dụng thuật toán Canny chỉ cần sử dung câu lệnh đơn giản sau:

import cv2 import matplotlib.pyplot as plt image = cv2.imread('cameraman.png', 0) edges = cv2.Canny(image, 100, 200) plt.imshow(edges, cmap='gray')

Với ảnh cameraman.png bạn có thể tải về máy:

Và kết quả nó sẽ như sau:

Bạn có hiểu rõ hơn các tham số của hàm Canny() trong tài liệu cv2.Canny

Tài liệu tham khảo

1. Xử lý ảnh - Lê Thanh Hà Chương 6
2. R. C. Gonzalez, R. E. Woods, “Digital Image Processing,” 4th edition, Pearson, 2018.
3. Slide
4. Code github: here
5. http://deeplearning.net/software/theano/tutorial/conv_arithmetic.html
6. Feature extraction (Edge, Line, Texture)
7. https://minhng.info/tutorials/xu-ly-anh-opencv-hien-thuc-canny-edge.html
8. https://towardsdatascience.com/canny-edge-detection-step-by-step-in-python-computer-vision-b49c3a2d8123