Viết Phương Trình Tiếp Tuyến Của đường Tròn Vuông Góc ... - KhoiA.Vn
Có thể bạn quan tâm
Khối A (KhoiA) sẽ giới thiệu với các em cách viết viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng cho trước qua bài này một cách ngắn gọn, chi tiết và đẩy đủ để các em tham khảo.
I. Cách viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng
Giả sử đường tròn (C) có tâm I(a; b); bán kính R và và đường thẳng (d) cho trước
Viết phương trình tiếp tuyến của (C) vuông góc với đường thẳng (d):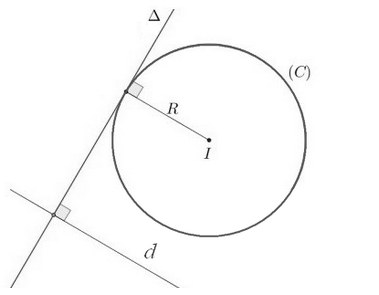 Để viết phương trình tiếp tuyến Δ của đường tròn (C) vuông góc với đường thẳng (d): Ax + By + C = 0 ta thực hiện như sau:
Để viết phương trình tiếp tuyến Δ của đường tròn (C) vuông góc với đường thẳng (d): Ax + By + C = 0 ta thực hiện như sau:
- Bước 1: Xác định tâm I và bán kính R của đường tròn (C).
- Bước 2: Vì Δ ⊥ (d): Ax + By + C = 0 nên Δ có vectơ pháp tuyến là vectơ chỉ phương của (d):
Khi đó phương trình tiếp tuyến Δ có dạng: Bx - Ay + c1 = 0
- Bước 3: Vì Δ tiếp xúc với đường tròn (C) nên d(I,Δ) = R. Giải phương trình này ta tìm được c1.
II. Bài tập vận dụng viết phương trình tiếp tuyến của đường tròn vuông góc với đường thẳng
* Bài tập 1 (Bài 6 trang 84 SGK Hình học 10): Cho đường tròn C có phương trình: x2 + y2 – 4x + 8y – 5 = 0
Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng: 3x – 4y + 5 = 0.
> Lời giải:
- Ta có: x2 + y2 – 4x + 8y – 5 = 0
⇔ (x2 – 4x + 4) + (y2 + 8y + 16) = 25
⇔ (x – 2)2 + (y + 4)2 = 25.
Vậy (C) có tâm I(2 ; –4), bán kính R = 5.
- Gọi tiếp tuyến vuông góc với đường thẳng (d): 3x – 4y + 5 = 0 cần tìm là (Δ).
- Ta có (d) có VTPT
- Vì (Δ) ⊥ (d) nên có VTPT
Vậy phương trình tiếp tuyến (Δ) có dạng: 4x + 3y + c = 0.
(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.
* Bài tập 2: Viết phương trình tiếp tuyến của đường tròn (C): x2 + y2 - 4x + 8y - 5 = 0. Biết tiếp tuyến vuông góc với đường thẳng (d); 3x + 4y + 21 = 0
> Lời giải:
- Ta có: x2 + y2 - 4x + 8y - 5 = 0
⇔ (x2 - 4x + 4) + (y2 + 2.4y + 16) - 25 = 0
⇔ (x - 2)2 + (y + 4)2 = 52
Nên đường tròn (C) có tâm I(2;-4) và bán kính R = 5.
Tiếp tuyến Δ vuông góc với (d): 3x+ 4y + 21 = 0 nên Δ nhận VTCP của (d) làm VTPT, có:
Khi đó phương trình tiếp tuyến Δ có dạng: 4x - 3y + c = 0.
Vì Δ tiếp xúc với đường tròn (C) nên khoảng cách từ tâm I tới đường thẳng Δ bằng R: d(I,Δ) = R
Vậy có 2 tiếp tuyến thỏa yêu cầu là:
4x - 3y + 5 = 0 và 4x - 3y - 45 = 0.
Từ khóa » Tìm Phương Trình Tiếp Tuyến Vuông Góc Với đường Thẳng
-
Viết Phương Trình Tiếp Tuyến Biết Tiếp Tuyến Vuông Góc Với đường ...
-
Cách Viết Phương Trình Tiếp Tuyến Vuông Góc Với đường Thẳng | Học
-
Viết Phương Trình Tiếp Tuyến Khi Biết Hệ Số Góc Hoặc Song Song ...
-
Viết Phương Trình Tiếp Tuyến Vuông Góc Với đường Thẳng Lớp 11
-
Viết Phương Trình Tiếp Tuyến Với đồ Thị (C), Biết Tiếp Tuyến Vuông Góc ...
-
Tiếp Tuyến Vuông Góc Với đường Thẳng
-
Chuyên đề Cách Viết Phương Trình Tiếp Tuyến Và Các Dạng Bài Tập
-
Viết Phương Trình Tiếp Tuyến Vuông Góc Với đường Thẳng Của đồ Thị ...
-
Cách Viết Phương Trình Tiếp Tuyến Vuông Góc Với Đường Thẳng ...
-
Phương Trình Tiếp Tuyến Vuông Góc Với Một đường Thẳng
-
Phương Trình Tiếp Tuyến Vuông Góc Với Đường Thẳng, Tổng Hợp ...
-
Phương Trình Tiếp Tuyến đường Tròn Vuông Góc Với đường Thẳng
-
Gọi Là đồ Thị Của Hàm Số Tiếp Tuyến Của Vuông Góc Với đường Thẳng ...