Vòng Tròn Lượng Giác
Có thể bạn quan tâm
Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.
Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ ZaloVòng tròn lượng giác và cách sử dụng vòng tròn lượng giác
- 1. Góc lượng giác và số đo góc lượng giác
- 2. Vòng tròn lượng giác và hướng dẫn sử dụng vòng tròn lượng giác
- 2. Dấu của các giá trị lượng giác
- 3. Bảng giá trị lượng giác từ đến
- 4. Công thức các cung liên kết trên đường tròn lượng giác
- 5. Bài tập vận dụng vòng tròn lượng giác
- Tài liệu học tập SGK Ngữ văn lớp 10 Mới
VnDoc.com xin giới thiệu tới quý thầy cô và các bạn học sinh tài liệu tham khảo Vòng tròn lượng giác để bạn đọc cùng tham khảo và có thêm tài liệu học tập nhé.
1. Góc lượng giác và số đo góc lượng giác
a) Góc lượng giác
Cho hai tia Ou, Ov.
Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ tia Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov. Kí hiệu: (Ou, Ov).
Minh họa
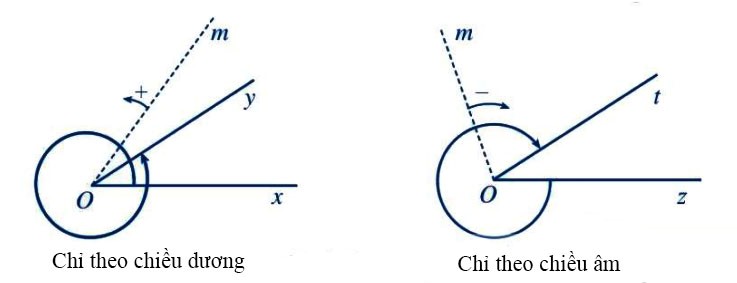
Chú ý:
Khi tia Om quay góc a0 thì góc lượng giác mà tia đó quét được có số đo a0, (tương tự với rad).
Nếu góc lượng giác (Ou, Ov) có số đo a0 thì ta kí hiệu sđ(Ou, Ov) = a hoặc (Ou, Ov) = a.
Mỗi một góc lượng giác gốc O xác định bởi tia đầu Ou và tia cuối Ov và số đo của góc đó.
Minh họa:
b) Tính chất của góc lượng giác
Cho hai góc lượng giác (Ou, Ov); (O’u’, O’v’) có tia đầu trùng nhau (Ou ≡ O’u’) tia cuối trùng nhau (Ov≡ O’v’). Khi đó nếu sử dụng đơn vị đo là độ thì ta nói:

Nếu sử dụng đơn vị đo là radian thì công thức trên có thể viết như sau:

Với ba tia tùy ý ![]() ta có:
ta có:
![]()
Ví dụ: Cho góc lượng giác (Ou, Ov) có số đo ![]() . Hỏi trong các góc
. Hỏi trong các góc ![]() những góc nào có số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho?
những góc nào có số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho?
Hướng dẫn giải
Ta có:
![]()
![]()
![]()
![]()
![]()
Nhận thấy số đo của một góc lượng giác có tia đầu và tia cuối với góc đã cho khi ta quay góc đó chẵn 1 vòng mà 1 vòng có số đo ![]()
Suy ra những góc thỏa mãn yêu cầu đề bài là ![]() .
.
Đơn vị radian
Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một chung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (hay 1rad).
Công thức chuyển đổi góc sang radian và ngược lại:
Ví dụ: a) Đổi từ độ sang radian các số đo sau: ![]()
b) Đổi từ radian sang độ các số đo sau: ![]() .
.
Hướng dẫn giải
a) Ta có:
b) Ta có:  .
.
2. Vòng tròn lượng giác và hướng dẫn sử dụng vòng tròn lượng giác
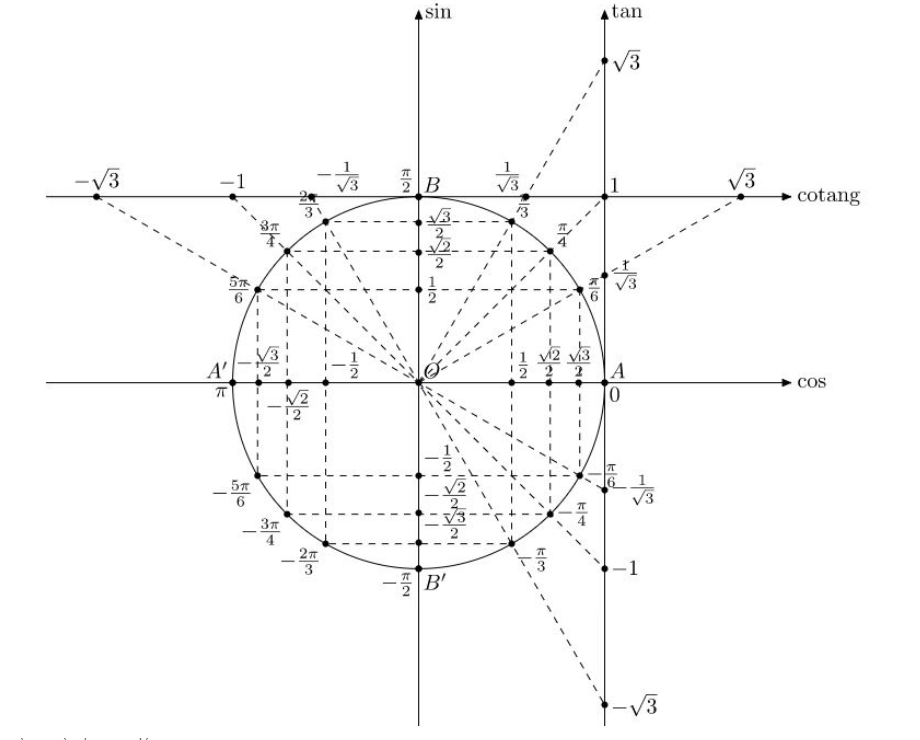
Vòng tròn lượng giác cơ bản đầy đủ chi tiết
- Vòng tròn lượng giác là đường tròn đơn vị tâm O bán kính 1, định hướng với quy ước chiều dương là chiều ngược chiều kim đồng hồ và trên đó A là điểm gốc.
- Điểm ![]() trên đường tròn lượng giác sao cho một điểm C bất kì nằm trên đường tròn ta đều có
trên đường tròn lượng giác sao cho một điểm C bất kì nằm trên đường tròn ta đều có ![]() được gọi là điểm trên đường tròn lượng giác biểu diễn cung lượng giác có số đo
được gọi là điểm trên đường tròn lượng giác biểu diễn cung lượng giác có số đo ![]() .
.
- Trục Ox được gọi là trục giá trị cos.
- Trục Oy được gọi là trục giá trị sin.
- Trục tan có gốc là điểm và vuông góc với trục cos, trục cotan có gốc là điểm vuông góc với trục sin.
Ví dụ: Xác định điểm P trên đường tròn lượng giác sao cho ![]() .
.
Hướng dẫn giải
Gọi điểm M là điểm chính giữa của cung A’B’ trên đường tròn lượng giác.
Ta có: ![]() được biểu diễn như hình vẽ sau:
được biểu diễn như hình vẽ sau:

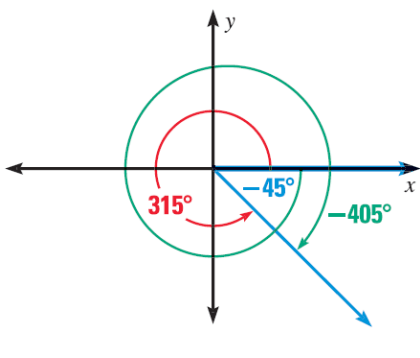
Ví dụ: Biểu diễn trên đường tròn lượng giác các góc -450 và góc 4800.
Hướng dẫn giải
a) Biểu diễn góc -450

b) Ta có: ![]()
Biểu diễn góc 4800 như sau:
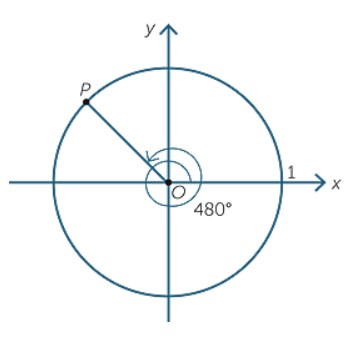
Trắc nghiệm: Trên đường tròn lượng giác gốc A. Cho điểm M xác định bởi ![]()
Giá trị lượng giác của góc lượng giác
a) Định nghĩa
Giả sử điểm ![]() là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo
là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo  (như hình vẽ):
(như hình vẽ):
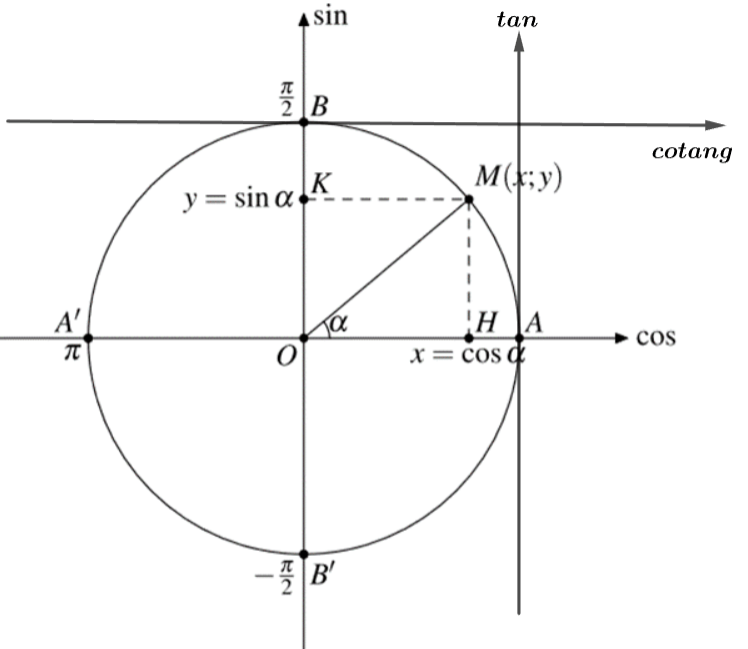
-
Hoành độ

-
Tung độ

-
 hay
hay  xác định khi
xác định khi 
-
 hay
hay  xác định khi
xác định khi 
2. Dấu của các giá trị lượng giác
| Góc phần tư số | I | II | III | IV |
| Giá trị lượng giác | ||||
| sin x | + | + | - | - |
| cos x | + | - | - | + |
| tan x | + | - | + | - |
| cot x | + | - | + | - |
Ví dụ: Xét dấu các giá trị lượng giác ![]() .
.
Hướng dẫn giải
Giả sử điểm M trên đường tròn lượng giác sao cho ![]()
Do ![]() nên điểm M thuộc góc phần tư thứ II.
nên điểm M thuộc góc phần tư thứ II.
Do đó 
Ví dụ: Tính giá trị biểu thức: ![]()
Hướng dẫn giải
Ta có:
![]()
![]()
3. Bảng giá trị lượng giác từ  đến
đến 
|
|
|
|
|
|
|
|
|
|
|
| |
| 0 | 0 | -1 | 0 | ||||||||
| 1 | 0 | -1 | 0 | 1 | |||||||
| 0 | 1 | || | -1 | 0 | || | 0 | |||||
| || | 1 | 0 | -1 | || | 0 | || |
4. Công thức các cung liên kết trên đường tròn lượng giác
| Góc đối nhau ( cos đối) | Góc bù nhau (sin bù) | Góc phụ nhau (Phụ chéo) | Góc hơn kém (Khác pi tan) |
| cos (-α) = cos α | sin (π-α) = sin α | sin (π/2-α)= cos α | sin (π+α) = - sin α |
| sin (-α) = -sin α | cos (π-α) = - cos α | cos (π/2-α) = sinα | cos (π+α) = - cosα |
| tan (-α) = - tan α | tan (π-α) = - tan α | tan (π/2-α) = cot α | tan (π+α) = tanα |
| cot (-α) = -cot α | cot (π-α) = – cot α | cot (π/2-α) = tan α | cot (π+α) = cotα |
Ví dụ: Rút gọn các biểu thức sau:
a) ![]()
b) ![]()
Hướng dẫn giải
a) ![]()
![]()
![]()
![]()
b) ![]()
![]()
![]()
![]()
5. Bài tập vận dụng vòng tròn lượng giác
Câu 1: Trên đường tròn lượng giác, số các điểm ngọn của cung có số đo bằng ![]() là:
là:
| A. 2 | B. 3 | C. 5 | D. 6 |
Câu 2: Trên đường tròn lượng giác, điểm ngọn của cung có số đo 30000 nằm ở góc phần tư thứ mấy?
| A. I | B. II | C. III | D. IV |
Câu 3: Cho góc α biết ![]() , chọn đáp án đúng trong các đáp án dưới đây?
, chọn đáp án đúng trong các đáp án dưới đây?
| A. cos α > 0, sin α > 0 | B. cos α > 0, sin α < 0 |
| C. cos α < 0, sin α > 0 | D. cos α < 0, sin α < 0 |
Câu 4: Trên đường tròn lượng giác cho các cung lượng giác (I), (II), (III) và (IV) có điểm đầu là A và có số đo lần lượt là:
| (a) | (b) | (c) | (d) |
Hỏi các cung nào có điểm cuối trùng nhau?
| A. Chỉ (a) và (b) | B. Chỉ (a), (b), (c) |
| C. Chỉ (b), (c), (d) | D. Chỉ (a), (b) và (d) |
Câu 5: Biết một góc lượng giác (Ou, Ov) có số đo ![]() . Góc lượng giác (Ou, Ov) âm lớn nhất là:
. Góc lượng giác (Ou, Ov) âm lớn nhất là:
| A. -1,6π | B. -27,6π | C. -0,6π | D. -0,4π |
Gợi ý tham khảo:
- Bài tập trắc nghiệm Công thức lượng giác – Có đáp án
- Bài tập trắc nghiệm Giá trị lượng giác của góc lượng giác – Có đáp án
- Bài tập trắc nghiệm Tỉ số lượng giác của góc nhọn
- Bài tập tính giá trị lượng giác của một góc lượng giác
- Bài tập đổi đơn vị góc lượng giác
- Trắc nghiệm Toán 10 Giá trị lượng giác của một góc từ 0 đến 180 độ (mức TH - VD)
- Chứng minh biểu thức lượng giác không phụ thuộc vào biến x Toán 10
-------------------------------------------------------------------
Trên đây VnDoc đã chia sẻ đến các bạn học sinh Vòng tròn lượng giác nhằm cung cấp cơ sở kiến thức ôn tập cho các bạn học sinh, giúp các bạn tiếp xúc với nhiều dạng bài về hàm số lượng giác. Bài viết cho chúng ta thấy được khái niệm vòng tròn lượng giác và hướng dẫn sử dụng vòng tròn lượng giác, dấu của giá trị lượng giác, bảng giá trị lượng giác, bên cạnh đó còn có các bài tập vận dụng... Hi vọng qua bài viết bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10 nhé. Chúc các bạn ôn tập thật tốt!
Tham khảo thêm
-
Luyện tập Phản ứng hạt nhân và năng lượng liên kết (dễ)
-
Trắc nghiệm đúng sai Công nghiệp hạt nhân
-
Luyện tập Công nghiệp hạt nhân (Trung bình)
-
Trắc nghiệm đúng sai Phản ứng hạt nhân và năng lượng liên kết
-
Luyện tập Phản ứng hạt nhân và năng lượng liên kết (Trung bình)
-
Trắc nghiệm đúng sai Hiện tượng phóng xạ
-
Phân phối chương trình Toán 10 năm 2020 - 2021
-
Luyện tập Phản ứng hạt nhân và năng lượng liên kết (khó)
-
Luyện tập Công nghiệp hạt nhân (Dễ)
-
Luyện tập Công nghiệp hạt nhân (Khó)
Từ khóa » Công Thức đường Tròn Lượng Giác
-
Cung Liên Kết- Phần Kiến Thức đường Tròn Lượng Giác Lớp 11 Nhất định Phải Thuộc.
-
Đường Tròn Lượng Giác - Một Số Kết Quả Cần Nhớ
-
Công Thức Lượng Giác - Giá Trị Lượng Giác Của Góc Lớp 10
-
Phương Pháp Đường Tròn Lượng Giác Vật Lý 12 - Kiến Guru
-
[ Đường Tròn Lượng Giác ] Những Thông Tin Và Một Số Lưu ý Khi Dùng
-
Kiến Thức Cần Nhớ: Đường Tròn Lượng Giác Vật Lý 12 | Lessonopoly
-
Vòng Tròn Lượng Giác
-
Vòng Tròn Lượng Giác Cơ Bản Và Hướng Dẫn Sử Dụng Chi Tiết
-
Đường Tròn Lượng Giác - Tỷ Mỷ Làm Toán. Độc Lập Suy Nghĩ.
-
Lý Thuyết Phương Trình đường Tròn | SGK Toán Lớp 10
-
Lý Thuyết Tổng Hợp Chương Cung Và Góc Lượng Giác. Công Thức ...
-
Khái Niệm Về Vòng Tròn Lượng Giác Là Gì? - Legoland
-
Công Thức Lượng Giác đầy đủ Nhất Cho Lớp 9, Lớp 10, Lớp 11